Задачи изучения математики. Стр 1 из 3Следующая ⇒ Задачи изучения математики.   1. Знать основные понятия и методы исследования и решения задач читаемой дисциплины. 2. Уметь применять математические методы к решению задач; проводить конкретные расчеты в рамках выполнения аудиторных и домашних заданий. 3. Иметь представление о математической символике для выражения количественных и качественных соотношений объектов; о применении теоретических рассуждений при доказательстве теорем. Общие рекомендации студенту по работе над курсом математики.   Самостоятельная работа над учебным материалом состоит из следующих элементов: 1. Изучение материала по лекциям. 2. Изучение материала по учебнику. 3. Выполнение еженедельных домашних заданий. 4. Выполнение контрольных домашних заданий (КДЗ). Студент может обращаться к преподавателю для получения консультации, посещать имеющиеся факультативные занятия. Указания к выполнению КДЗ. 1. Каждое контрольное домашнее задание должно выполняться в отдельной тонкой тетради в клетку, чернилами черного или синего цвета. Необходимо оставлять поля шириной 6 см. для замечаний преподавателя. 2. На титульном листе тетради должны быть четко написаны фамилия студента, его инициалы, название дисциплины, номер выполняемого варианта. Как правило, номер варианта задается преподавателем. 3. Решения задач нужно располагать в порядке возрастания их номеров, обязательно записывая условия каждой задачи. 4. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 5. Оформление решения задачи следует завершать словом «Ответ». 6. После получения проверенной преподавателем работы студент должен в этой же тетради исправить все отмеченные ошибки и недочеты. Вносить исправления в сам текст работы после ее рецензирования запрещается.   ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №1 «Неопределенный и определенный интеграл» Вариант 0 I. Вычислить интегралы:                                                          II. Вычислить определённые интегралы: 1. 2.  ; 3.   III. Вычислить несобственные интегралы или доказать их расходимость: 1.               IV. Вычислить площади фигур, ограниченных линиями: 1.  ; y=1                            I. Решение   1. = = (получили сумму табличных интегралов ) =  + c   2.   = = arcsin   3.  =  =   =  x + sinx + c   4.  = =   5.   =  3   =  3 Для вычисления этих интегралов пользовались основной таблицей интегралов, формулами тригонометрии,  действиями со степенями и дробями.   6.  = известно, что ) = , тогда                                                                              имеем свойство дифференциала    т.е.   = (-cos (1- )) + c  = cos (1- ) + c    7. = =      = имеем формулу   sin , тогда   =  =  =   9.  = выделим полный квадрат в знаменателе  = = =   10. = воспользуемся формулой интегрирования по частям   Пусть →                    dV = dx → V = x Имеем:          посчитаем получившийся интеграл   =         , замена   = = = =              t arctgt    = Получаем:   II. Вычислить определенные интегралы. Нам понадобятся формула Ньютона-Лейбница и правила пользования заменой и формулой интегрирования по частям в определённом интеграле.   1. )   2.  =                   т. к. ,    то   Необходимо пересчитать пределы интегрирования    =  =  =  =   III. Вычислить несобственные интегралы или доказать их расходимость. 1. = Подинтегральная  функция имеет разрыв     (не определена)         в точке .       Тогда     Следовательно, интеграл расходится. 2. Известно,  что     III. Вычислить площадь фигур, ограниченных линиями. S -2 2 4 A B a b 1. Сделаем рисунок. Кривые заданы в декартовой системе координат, следовательно, Найдем пределы интегрирования . Для этого решим совместно Получаем S = 2. Сделаем рисунок. Кривая задана в полярных координатах. 3 S Это известная кривая – четырехлистник, которую можно построить по точкам. Но воспользуемся ее свойствами.           Удобнее записать   Имеем 4 зоны, т.е. 4 лепестка.   Воспользуемся симметричностью этих лепестков. Тогда вся площадь  , где  – заштрихованная площадь. Здесь  меняется в интервале . Имеем:   Тогда S = КОНТРОЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ №1   Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9

Вариант 10

Вариант 1 1

Вариант 12

Вариант 13

Вариант 14

Вариант 15

Вариант 16

Вариант 17

Вариант 18

Вариант 19

Вариант 20

Вариант 2 1

Вариант 22

Вариант 23

Вариант 24

Вариант 25

 

Вариант 1

Вариант 2

Вариант 3

 

Вариант 4		Вариант 5		Вариант 6

 

Вариант 7		Вариант 8		Вариант 9

 

Вариант 10		Вариант 11		Вариант 12

 

Вариант 13		Вариант 14		Вариант15

 

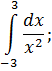
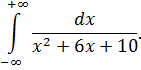
Вариант 16		Вариант 17		Вариант 18

 

Вариант 19		Вариант 20		Вариант 21

 

Вариант 22		Вариант 23		Вариант 24

 

Вариант 25

 

IV.

1.
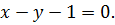
2.
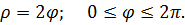
3.
4.
5.
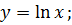
6.
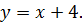
7.
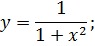
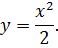
8.
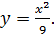
9.
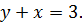
10.
11.
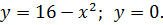
12.
13.
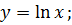
14.
15.
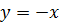
16.
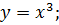
17.
18.
19.
20.
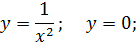
21.
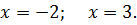
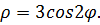
22.
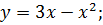
23.
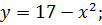
24.
25.

 

ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №2

«Дифференциальные уравнения»

 

Вариант 0

I. Решить уравнение .

 

II. Найти общее решение уравнения .

 

III. Найти общее решение уравнения:

а)

б)

 

IV. Найти общее решение уравнения (без нахождения неопределенных коэффициентов).

а)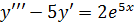

б)

 

V.  Решить задачу Коши.

     y (0) = 0 ; y ’ (0) = 0

 

VI. Найти общее решение уравнения методом вариации произвольных постоянных.

 

Решение.

I.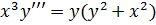

Разделим обе части уравнения на х³, получим

Правая часть этого уравнения есть функция отношения ,   

следовательно , это однородное уравнение.

Обозначим и

 

Имеем: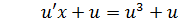

 

- это уравнение с разделяющимися переменными

Интегрируем:

.          Подставим

Если константу С записать в другом виде « », то общее решение будет иметь вид:

В процессе решения мы делили обе части уравнения на  х³≠0 и  u³ ≠0 и могли потерять решения  х=0 и u=0 ( u=0  =0 y=0)

Непосредственной проверкой убеждаемся , что  х  = 0 не является решением;  а  у = 0 – решение,  которое не входит в общий интеграл ни при каком С

Имеем ответ: ;    у=0.

 

II.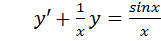

Это линейное уравнение

Пусть

Имеем

– уравнение с разделяющими переменными.

, 

 

т.к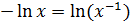  

,    подставим найденное     u

Интегрируем

Тогда

Ответ: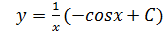

 

III.   a)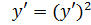

Это уравнение второго порядка, не содержащее функцию у.

Положим

Уравнение имеет вид 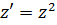 – это уравнение с разделяющимися        переменными.  .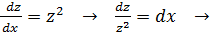

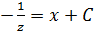Вернемся  к    у , получаем

 

Это и будет ответом.

 

б)

Это уравнение второго порядка, не содержащее Х.

Положим

Имеем p ( p ’ 2 y ) = 0

1) p = 0 = 0 y = C

2)

 

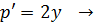
Ответ: y=C;

 

IV.   а)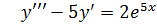

Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами.

1) Рассмотрим однородное уравнение: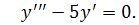

Составим характеристическое уравнение и найдем его корни

    k³ - 5k = 0 k(k²-5) = 0 k₁ = 0 k_2,3 = ±

 Следовательно ,

 

 - oбщее решение однородного уравнения в случае действительных  различных корней характеристического уравнения.

2) Правая часть неоднородного уравнения ;  – многочлен нулевой степени,  (α – не является корнем характеристического уравнения).  Тогда  – частное решение неоднородного уравнения.

3) Найдем неопределенный коэффициент  А

Имеем

 

Подставим найденные производные в исходное уравнение

. Известно, что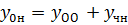

 

Ответ:

 

б) Найти вид общего решения уравнения

1). Составим характеристическое уравнение и найдем его корни:

если корни характеристического уравнения комплексны  α±β , то

 

 

 

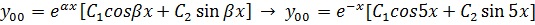
2). Правая часть уравнения имеет вид:

,   где

- многочлен степени 2

- многочлен степени 1

Для правой части нашего уравнения

 

,

здесь  многочлен 2-ой степени c неопределенными коэффициентами.

3) Общее решение неоднородного уравнения   y_0н  есть сумма общего решения однородного уравнения  y₀₀ и частного решения неоднородного уравнения    y_чн     y_0н=y₀₀+y_чн

Имеем

 

V.  ; ;

1) Найдем y₀₀ для уравнения

Характеристическое уравнение k² - 2k = 0 k₁ = 0; k₂ = 2

Корни действительны и различны, следовательно,

 

2) Найдем   y_чн , ;  – многочлен,  α = 0.

Значит,

Множитель Х появляется из-за того, что  α = 0 есть однократный корень характеристического уравнения.

 

3) Найдем коэффициенты A, B, C

          

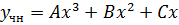
Подставим в уравнение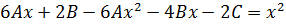

 

Отсюда:   → 

4) Чтобы решить задачу Коши, нужно найти  С₁  и  С₂ , воспользовавшись начальными условиями:

Ответ:  – искомое решение.

 

VI.

1) Рассмотрим однородное уравнение и найдем корни его характеристического уравнения

т.е. функции и будут частными решениями этого однородного уравнения.

2) Запишем решение неоднородного уравнения в виде:

 

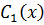  и составим систему уравнений для нахождения и

 

 

Применим метод Крамера для решения системы:

 

 

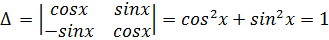
Тогда

   

 

Ответ: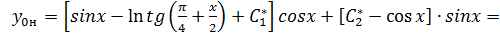

               

 

 

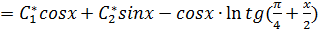
КОНТРОЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ №2

I. Найти общее решение уравнения:

1.

 

2.

 

3.

 

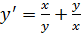
4.

 

5.

 

6.

 

7.

 

8.

 

9.

 

10.

 

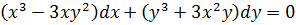
11.

 

12.

 

13.

 

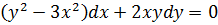
14.

 

15.

 

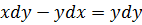
16.

 

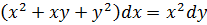
17.

 

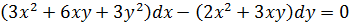
18.

 

19.

 

20.

 

21.

 

22.

 

23.

 

24.

 

25.

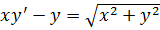
I. Найти общее решение уравнения:

1.

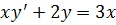
2.

3.

4.

5.

6.

7.

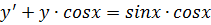
8.

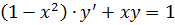
9.

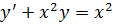
10.

11.

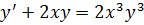
12.

13.

14.

15.

16.

17.

18.

19.

20.

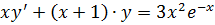
21.

22.

23.

24.

25.

 

 

II. Найти общее решение уравнения:

1. а) ;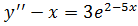 

б) , y (0) = - 1 , y ’(0) = 1

2. а) ;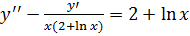 

б)

 

3. а)  

 б)

 

4. а)  

б)

 

5. а)  

 б)

 

6. а)  ;

б)

 

7. а) ;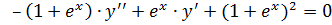

б)

 

8. а)  

б) 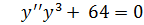 , y (0)  = 4, y ’(0) = 2

9. а)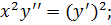  

б)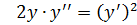

10. а) ; 

б)

 

11. а)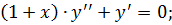  

б)

 

12. а)  

 б)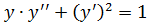

 

13. а)  

б)

 

14. а)  

 б)

 

15. а)  

 б)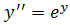

 

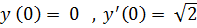
16. а)  

б)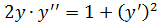

 

17. а)  

б)   

 

18. а)  

б)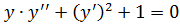

 

19. а) ;

  б)

 

20. а)  ;

б)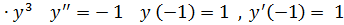

 

21. а) ; 

б)

 

22. а)  ;

 б)

 

      23. а)  ;

 б)

 

24. а)  

 б)  +1

    25. а)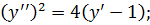  

 б)

 

V . Решить задачу Коши

1.

2.     

3.

4.

5.

6.

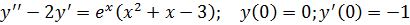
7.

8.

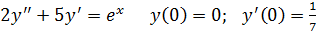
9.      

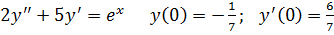
10.

11.

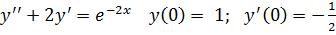
12.

13.

14.

15.

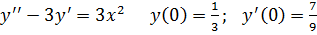
16.

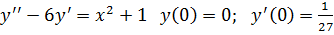
17.

18.

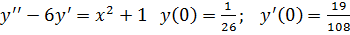
19.

20.

21.

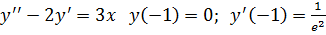
22.

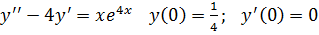
23.

24.

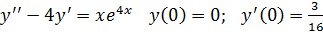
25.

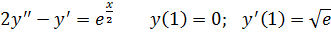
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Данко П.Е. и др. Высшая математика в упражнениях и задачах

ч. I и II     –М . Айрис-пресс 2008.

2. Письменный Д.Г. Конспект лекций по высшей математике.

Полный курс. –М.-Айрис-пресс 2007.

 

3. Самохин А.В. и др. Сборник задач по высшей математике

ч. IV. Интегралы. Дифференциальные уравнения. – М. РИО МГТУ ГА 2005. №1448

Задачи изучения математики.

 

1. Знать основные понятия и методы исследования и решения задач читаемой дисциплины.

2. Уметь применять математические методы к решению задач; проводить конкретные расчеты в рамках выполнения аудиторных и домашних заданий.

3. Иметь представление о математической символике для выражения количественных и качественных соотношений объектов; о применении теоретических рассуждений при доказательстве теорем.

Общие рекомендации студенту по работе над курсом математики.

 

Самостоятельная работа над учебным материалом состоит из следующих элементов:

1. Изучение материала по лекциям.

2. Изучение материала по учебнику.

3. Выполнение еженедельных домашних заданий.

4. Выполнение контрольных домашних заданий (КДЗ).

Студент может обращаться к преподавателю для получения консультации, посещать имеющиеся факультативные занятия.

123Следующая ⇒

Поделиться: