
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Следствие2: Если две функции имеют разные производные в некотором промежутке. То они отличаются в этом промежутке лишь постоянным слагаемым. ⇐ ПредыдущаяСтр 3 из 3
Если, В силу следствия1: Среднее значение функции — это некоторое число, заключённое между наименьшим и наибольшим её значениями. В дифференциальном и интегральном исчислении имеется ряд «теорем о среднем», устанавливающих существование таких точек, в которых функция или её производная получает то или иное среднее значение. Наиболее важной теоремой о среднем значении функции в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если f(x) непрерывна на отрезке [a,b] и дифференцируема в интервале (a,b), то существует точка c, принадлежащая интервалу (a,b), такая, что f(b) − f(a) = (b − a)f'(c). В интегральном исчислении наиболее важной теоремой о среднем значении является следующая: если f(x) непрерывна на отрезке [a,b], а
В частности, если
Вследствие этого под средним значением функции f(x) на отрезке [a,b] обычно понимают величину
Аналогично определяется среднее значение функции нескольких переменных в некоторой области. №23. Выпуклость вогнутость функции. Точки перегиба. Необходимые и достаточные условия. Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 ( a, b ). Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x0 , f ( x0 ) ), x0 ( a, b ). Достаточное условие вогнутости ( выпуклости ) функции. Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда: если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b ); если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) . Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0. №24. Теорема Кронекера – Капелли. Решение однородных систем линейных алгебраических уравнений. Фундаментальная система решений. Теорема Кронекера-Капелли: для того, чтобы СЛАУ имела решение (была совместной) необходимо и достаточно, чтобы ранг её расширенной матрицы был равен рангу основной матрицы. r ( A | b ) = r ( A ) Решение однородных систем. Однородная система всегда совместна, её тривиальным решением является 0-ой вектор. Для того чтобы СЛАУ имела не 0-ое решение необходимо и достаточно, чтобы r(A) был меньше числа неизвестных (r < n). Пусть основная матрица А однородной системы уравнений имеет ранг r, тогда эта система уравнений имеет n – r линейно независимых решений. Совокупность лин. нез. реш. одн. сис. уравнений называется фундаментальной системой решений (ФСР). Общая ФСР может быть записана в виде:
Алгоритм нахождения ФСР: 1) Составляем расширенную матрицу (А|b), находим её ранг (по Гауссу) 2) Преобразуем систему к эквивалентному виду (из полученной в первом пункте матрицы) 3) Выражаем зависимые переменные через независимые 4) Записываем ФСР №25. Теорема Кронекера – Капелли. Решение неоднородных систем линейных алгебраических уравнений. Структура общего решения. Теорема Кронекера-Капелли: для того, чтобы СЛАУ имела решение (была совместной) необходимо и достаточно, чтобы ранг её расширенной матрицы был равен рангу основной матрицы. r ( A | b ) = r ( A ) Неоднородной системой линейных уравнений называется система вида:
Пусть r(A | b) = r(A) (т.е. система (2) совместна), тогда: если r = n, где n – число переменных системы (2), то решение существует и оно единственно; если r < n, то общее решение системы (2) имеет вид №26. Методы решения систем линейных алгебраических уравнений с квадратной основной матрицей . Системы решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера;3) матричным методом. Метод Гаусса Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Формулы Крамера Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А Δ = det (aij) и n вспомогательных определителей Δi (i = Формулы Крамера имеют вид: Δ · xi = Δi (i = Из (1) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: xi = Δi / Δ. Если главный определитель системы Δ и все вспомогательные определители Δi = 0 (i = Матричный метод Если матрица А системы линейных уравнений невырожденная, т.е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X = C, C = A-1B называют матричным способом решения системы, или решением по методу обратной матрицы. №27. Представление чисел в памяти ЭВМ. Приближенные числа. Погрешность решения вычислительных задач, ее источники. Существуют два способа представления чисел в памяти ЭВМ. Они называются так: форма с фиксированной точкой и форма с плавающей точкой. Форма с фиксированной точкой применяется к целым числам, форма с плавающей точкой — к вещественным числам (целым и дробным). Под точкой здесь подразумевается знак-разделитель целой и дробной части числа. Приближенным числом а называется число, незначительно отличающееся от точного числа А и заменяющее его в вычислениях. Абсолютной погрешностью или, короче, погрешностью приближенного числа называется разность между этим числом и его точным значением Δx = |x – x0|. Относительной погрешностью приближённого числа называется отношение абсолютной погрешности приближённого числа к самому этому числу e(x)= Δx/ x0 Погрешность решения задачи обуславливается следующими причинами (источниками): 1. Математическое описание задачи является неточным, в частности, неточно заданы исходные данные описания.2. Применяемый для решения метод часто не является точным: получение точного решения задачи требует неограниченного или неприемлемо большого числа арифметических операций, и поэтому вместо получения точного решения приходится прибегать к приближенному.3. При выполнении арифметических операций на ЭВМ или любым другим образом, как правило, производятся округления. (Это же относится к вводу чисел в память ЭВМ и выводу полученных результатов.) Погрешности, соответствующие этим причинам, называются: неустранимая погрешность, погрешность метода, вычислительная погрешность. №28. Прямые вычислительные методы решения систем линейных алгебраических уравнений. Метод оптимального исключения. ыва №29. Итерационные вычислительные методы решения систем линейных алгебраических уравнений. Метод простой итерации. Рассмотрим систему:
Для неё итерационное вычисление буде т выглядеть так:
Сходимость методу будет осуществлять
Алгоритм: 1. Условие 2. Задаётся начальное приближение и точность 3. Вычисляется очередная итерация - Если - Иначе №30. Итерационные вычислительные методы решения не линейных уравнений. Метод бисекции. Метод простой итерации. Методы решения нелинейных уравнений (метод простой итерации, метод Ньютона, модифицированный метод Ньютона, метод секущих). Метод бисекции или метод деления отрезка пополам — простейший численный метод для решения нелинейных уравнений вида f(x)=0. Предполагается только непрерывность функции f(x). Теорема (Больцано — Коши).Пусть функция Следствие.Пусть функция
Таким образом, если мы ищем ноль, то на концах отрезка функция должна быть разных знаков. Разделим отрезок пополам и возьмём ту из половинок, для которой на концах функция по-прежнему принимает значения разных знаков. Если серединная точка оказалось искомым нулём, то процесс завершается.Если задана точность вычисления  , то процедуру следует продолжать до тех пор, пока длина отрезка не станет меньше , то процедуру следует продолжать до тех пор, пока длина отрезка не станет меньше  .Для поиска произвольного значения достаточно вычесть из значения функции искомое значение и искать ноль получившейся функции. Задача заключается в нахождении корней нелинейного уравнения .Для поиска произвольного значения достаточно вычесть из значения функции искомое значение и искать ноль получившейся функции. Задача заключается в нахождении корней нелинейного уравнения  Для начала итераций необходимо знать интервал [xL,xR] значений x, на концах которого функция принимает значения разных знаков: Для начала итераций необходимо знать интервал [xL,xR] значений x, на концах которого функция принимает значения разных знаков:  Из непрерывности функции f и условия (2) следует, что на интервале [xL,xR] существует хотя бы один корень уравнения (в случае наличия нескольких корней метод приводит к нахождению одного из них)Выберем точку внутри интервала Из непрерывности функции f и условия (2) следует, что на интервале [xL,xR] существует хотя бы один корень уравнения (в случае наличия нескольких корней метод приводит к нахождению одного из них)Выберем точку внутри интервала  Если f(xM) = 0, то корень найден. Если Если f(xM) = 0, то корень найден. Если 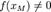 разобьём этот интервал на два [xL,xM] и [xM,xR]. Теперь найдём новый интервал, в котором функция меняет знак. Пусть разобьём этот интервал на два [xL,xM] и [xM,xR]. Теперь найдём новый интервал, в котором функция меняет знак. Пусть  и соответственно корень находится внутри интервала [xL,xM]. Тогда обозначим xR=xM и повторим описанную процедуру до достижения требуемой точности. За количество итераций N первоначальный отрезок делится в 2N раз. Метод простой итерации (метод последовательных повторений). Для применения метода простой итерации следует исходное уравнение и соответственно корень находится внутри интервала [xL,xM]. Тогда обозначим xR=xM и повторим описанную процедуру до достижения требуемой точности. За количество итераций N первоначальный отрезок делится в 2N раз. Метод простой итерации (метод последовательных повторений). Для применения метода простой итерации следует исходное уравнение  преобразовать к виду, удобному для итерации преобразовать к виду, удобному для итерации  . Это преобразование можно выполнить различными способами. Функция . Это преобразование можно выполнить различными способами. Функция 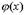 называется итерационной функцией. Расчетная формула метода простой итерации имеет вид: называется итерационной функцией. Расчетная формула метода простой итерации имеет вид:  . Теорема о сходимости метода простой итерации. Пусть в некоторой . Теорема о сходимости метода простой итерации. Пусть в некоторой  - окрестности корня - окрестности корня  функция функция 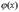 дифференцируема и удовлетворяет неравенству дифференцируема и удовлетворяет неравенству  , где , где  - постоянная . Тогда независимо от выбора начального приближения из указанной - постоянная . Тогда независимо от выбора начального приближения из указанной  - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится cо скоростью геометрической последовательности и справедлива оценка погрешности: - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится cо скоростью геометрической последовательности и справедлива оценка погрешности: 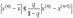 , ,  .Критерий окончания итерационного процесса. При заданной точности .Критерий окончания итерационного процесса. При заданной точности  >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство  . Если величина . Если величина  , то можно использовать более простой критерий окончания итераций: , то можно использовать более простой критерий окончания итераций:  .Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду .Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду  . Предположим дополнительно, что производная . Предположим дополнительно, что производная  знакопостояна и знакопостояна и  на отрезке [a,b]. Тогда при выборе итерационного параметра на отрезке [a,b]. Тогда при выборе итерационного параметра 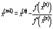 метод ходится и значение метод ходится и значение  . .
|
Последнее изменение этой страницы: 2019-04-19; Просмотров: 165; Нарушение авторского права страницы