Производная и ее геометрический и физический смысл.

  n°1. Понятие производной.

 

  Пусть и . Точка  называется внутренней точкой множества 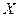, если она принадлежит ему вместе с некоторой своей окрестностью, т.е. существует такая окрестность  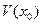точки , что .

  Пусть теперь функция  определена на множестве  и 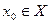 - внутренняя точка множества 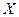.Тогда существует такая окрестность  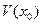точки , что  и, следовательно, функция

определена на множестве 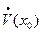 и  – точка сгущения этого множества. Таким образом, корректно следующее

  Определение 1. Если существует предел

,

то он называется производной функции  в точке .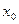  

  Производная функции  ( ) в точке  обозначается одним из следующих символов:

, , , ,

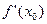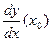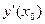при этом если ясно, в какой точке рассматривается производная, то для ее обозначения используют символы: , , , .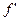

  Таким образом,

   

(1)

 

Замечание 1: Если положить 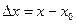, , 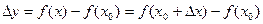то теорема о пределе суперпозиции позволяет также определить производную  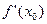с помощью любого из равенств:

,

(2)

 

.

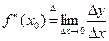(3)

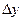Величины  и  называют, соответственно, приращением аргумента и приращением функции в точке 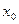. В соответствии с равенством (3), можно сказать, что производная  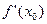равна пределу отношения приращения функции (в точке ) к приращению аргумента.

       Замечание 2: Определение производной выше было дано в предположении, что точка  - внутренняя точка области определения 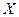 функции . Если же точка  не является внутренней точкой множества 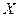, но принадлежит этому множеству вместе с некоторой своей односторонней окрестностью , или , то можно ввести понятие односторонней производной:

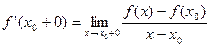 (правая производная)

 (левая производная).

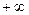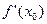Замечание 3: Если предел (1) равен  или , то производная  называется бесконечной.

       Теорема 1. Пусть функция  определена в окрестности точки 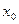 и имеет в этой точке конечную производную. Тогда она непрерывна в этой точке.

  Д о к а з а т е л ь с т в о. Достаточно заметить, что

 

 

 □

 

   § 2. Дифференцируемые функции. Понятие дифференциала и его геометрический и физический смысл.

Пусть функция  определена в окрестности точки .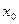

    Определение 1. Если существует такая линейная функция 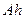 вещественного аргумента  ( ), что приращение  функции 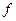 может быть представлено в виде

         

(1)

 

где 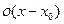 - бесконечно малая при  высшего порядка по сравнению с функцией  (т.е.  при 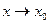), то функция  называется дифференцируемой в точке , а соответствующая линейная функция 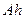 называется ее дифференциалом в этой точке.

  Дифференциал функции  в точке  обычно обозначается одним из символов:

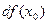 или .

В последнем случае имеют в виду, что , при этом часто опускают указание о том, в какой точке рассматривается этот дифференциал, т.е. для обозначения дифференциала используют символы  или . Таким образом,

.

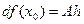(2)

 

  Замечание 1: Очевидно, равенство (1) можно записать в виде

         

(1’)

 

,

где , или, короче, в виде

         

(1’’)

где  - приращение функции в точке 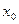, соответствующее приращению аргумента . Поэтому вместо (2) также пишут:

(2’)

т.е. трактуют аргумент  в (2) как переменное приращение аргумента функции  в точке .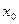

  Теорема 1. Для того, чтобы функция  была дифференцируемой в точке 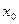, необходимо и достаточно, чтобы она имела в этой точке конечную производную .

  Д о к а з а т е л ь с т в о. Необходимость. Пусть функция  дифференцируема в точке . Тогда из равенства (1) следует, что

Это означает, что существует конечная производная

.

  Достаточность. Предположим, что в точке 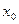 функция  имеет конечную производную 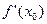. Тогда из равенства

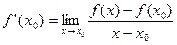
следует, что

,

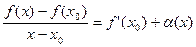(3)

где 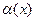 - бесконечно малая при  функция. Поэтому

(4)

и так как

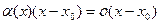
(ибо ),

то равенство (4) можно записать в виде:   

,

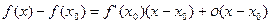(5)

 

т.е. в виде (1), где . Таким образом, функция  дифференцируема в точке . □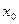

  Замечание 2: С учетом доказательства теоремы можно утверждать, что дифференциал функции в точке  есть следующая линейная функция от приращения аргумента :

.

(6)

А поскольку для функции 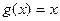 имеем  , то

,

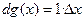 т.е.

,

то можно сказать, что-  - дифференциал  независимой переменной 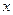 и, следовательно, определению дифференциала  можно придать форму:

.

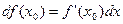(7)

Отсюда, в частности, становится понятным, почему для обозначения производной 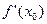 используют также обозначение .

       Геометрический смысл дифференциала: Нетрудно убедиться, что значение дифференциала 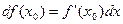 в точке  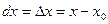равно приращению ординаты касательной к графику функции  в точке . Подробнее об этои см. учебники Фихтенгольца и Кудрявцева.

  Физический смысл дифференциала: Если  – длина пути, проходимого материальной точкой за время 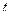, то дифференциал  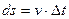 (  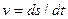– скорость в момент времени 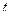) – путь, который она бы прошла за промежуток времени  при условии, что она бы двигалась на нем с постоянной скоростью, равной скорости 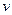 в момент времени . Если  – количество электричества, протекающее через поперечное сечение проводника в момент времени 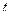, то дифференциал  (  – сила тока в момент времени 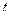) – количество электричества, которое протекло бы через это поперечно сечение за время , точнее от момента времени 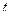 до момента времени , при условии, что сила тока была бы постоянной и равнялась силе тока в момент времени .

 

  §3. Арифметические операции с дифференцируемыми функциями.

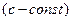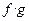  Теорема. Пусть функции  и  определены в окрестности точки  и дифференцируемы в этой точке. Тогда в этой точке дифференцируема и каждая из функций

, ,  и  (при ),

причем

         

,

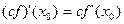(1)

         

,

(2)

      

,

(3)

      

.

(4)

 

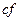
Д о к а з а т е л ь с т в о: 1. Дифференцируемость функции  и равенство (1) очевидно будут установлены, если будут установлены дифференцируемость функции 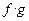 и равенство (3). В последнем случае достаточно будет рассмотреть функцию .

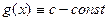2. Дифференцируемость функции  и равенство (2) вытекают из того, что имеют место равенства

и из того, что по условию существуют конечные пределы

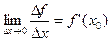 и ,

при этом следует помнить, что дифференцируемость функции в точке 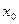 равносильна существованию конечной ее производной в этой точке.

3. Дифференцируемость произведения функций и равенство (3).

Пусть

.

 Тогда

,

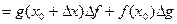и, следовательно,

.         

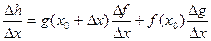
(5)

 

В силу дифференцируемости функций  и  в точке , существуют конечные пределы

,  и

(6)

Поэтому из (5) следует, что существует конечный предел

,

(7)

т.е. функция 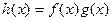 дифференцируема в точке 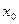. Переходя в равенстве (5) к пределу при  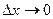с учетом равенств (6) и (7) получим равенство (3).

  4. Дифференцируемость  и равенство (4). Положим . По крайней мере, в некоторой окрестности точки 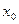, это определение корректно, так как  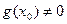и функция  непрерывна в точке .

  Далее, имеем:

,

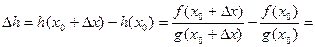
и, следовательно,

.

Рассуждая теперь аналогично пункту 3 данного доказательства, убеждаемся, что функция  дифференцируема в точке 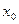, а переходя здесь к пределу при  получим также и равенство (4). □

      

  Замечание (о формулах для дифференциалов, вытекающих из формул (1) - (6)). Учитывая, что дифференциал функции  в точке 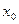 находится по правилу  из формул (1)–(4) , умножая каждую из них на , получим следующие формулы для дифференциалов:

 

(здесь );

 

;

 

;

 

.

 

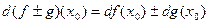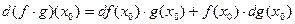 §4. Дифференцирование сложной функции.

1)     Напомним, что суперпозицию двух и более функций мы называем также сложной функцией.

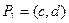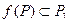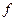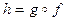    Теорема. Пусть функция  определена на интервале , а функция  определена на интервале , причем . Тогда если функция  дифференцируема в точке , а функция  дифференцируема в точке , то сложная функция  дифференцируема в точке  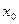и

(1)

    Д о к а з а т е л ь с т в о. В силу дифференцируемости функци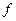й  и 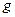, соответственно, в точках  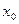и 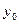, имеем

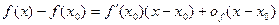
(2)

и

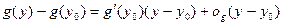
(3)

    Как известно

,

(4)

где 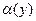 - бесконечно малая при , причем без ущерба для общности можно считать, что 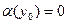, то есть можно считать, что функция  непрерывна в точке .

    Из (3) и (4) следует, что

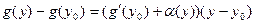
Подставляя сюда ,  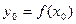и используя затем равенство (2), получим

и, следовательно,

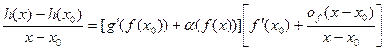
(5)

    Поскольку функция  непрерывна в точке , а функция 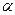 непрерывна в точке  и , то по теореме о непрерывности сложной функции

.

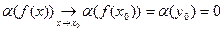А так как, кроме того,

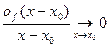
то из (5) следует, что существует конечная производная

и имеет место равенство (1). Для завершения доказательства теоремы остается вспомнить, что существование конечной производной  равносильно дифференцируемости функции 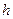 в точке . 

    Замечание. Пусть выполнены условия теоремы. Тогда по определению дифференциала

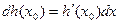
(6)

И, в силу равенства (1), для сложной функции будем иметь

или

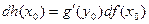
(7)

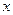Считая точку  произвольной (то есть заменяя  на произвольное ). Равенства (6) и (7) записывают в виде

	(6¢)
	(7¢)

Эти формулы показывают, что формально вид дифференциала не меняется как при записи его через независимую переменную 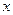, так и при записи через зависимую переменную . В этом состоит, так называемое, свойство инвариантности дифференциала, который называют также первым дифференциалом.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться: