Лабораторная работа №5 Двумерные данные ⇐ ПредыдущаяСтр 7 из 9Следующая ⇒ Изучить теорию Наборы двумерных данных содержат информацию о двух признаках (переменных) для каждого из объектов. В дополнение к изучению обобщающих характеристик каждой из этих двух переменных, рассматриваемых как отдельные наборы одномерных данных, статистические методы анализа двумерных данных используются для изучения связи между этими двумя переменными. При таком анализе необходимо выяснить следующие вопросы. Ü Существует ли между этими двумя переменными простая связь? Ü Насколько сильно взаимосвязаны переменные? Ü Можно ли предсказать значение одной переменной на основании другой? Если да, то с какой степенью надежности? Ü Существуют ли отдельные объекты или группа объектов, которые требуют особого внимания? При изучении зависимости между двумя переменными рекомендуется в качестве первоначальной цели провести визуальное исследование. Существует два вида численных анализа двумерных данных, представленных переменными X и Y: корреляционный анализ и ковариационный анализ, позволяющий оценить степень взаимосвязи между переменными X и Y,; регрессионный анализ, определяющий форму (вид) связи между этими переменными. Ниже рассмотрен корреляционный анализ Корреля́ ция (от лат. correlatio — соотношение, взаимосвязь), корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). Для визуального анализа зависимости между двумя переменными используются графики рассеяния. В Excel данный вид графиков называется точечной диаграммой или диаграммой рассеяния. Диаграмма рассеяния позволяет увидеть структуру двумерных данных. Если ваши данные содержат какие-то проблемы (например, выбросы), чаще всего единственный способ их обнаружения состоит как раз в анализе диаграммы рассеяния. При построении диаграмм рассеяния одна переменная (обозначается буквой Y) рассматривается как зависимая переменная, другая переменная (обозначается буквой X) является независимой переменной, оказывающей влияние на переменную Y. На диаграмме рассеяния переменой X соответствует горизонтальная ось, а переменной Y – вертикальная ось. Сформулировать задание на анализ Подготовить исходные данные Таблица 1. Объекты недвижимости Объект     Объект     26, 0 37, 2 31, 0 38, 4 37, 4 43, 6 34, 8 44, 8 39, 2 40, 6 38, 0 41, 8 39, 6 45, 2 31, 2         Ввести обозначения Независимой и зависимой переменных Введем обозначения: X – независимая переменная, определяющая размер жилой площади (в квадратных метрах); Y – зависимая переменная, определяющая цену продажи жилого объекта (в тысячах долларов). Расположите данные в столбцах Расположить необходимо таким образом, чтобы значения X были слева, а значения Y – справа Построить диаграмму Необходимо выбрать тип Точечная диаграмма Выполнить визуальный анализ полученной диаграммы Визуально можно определить имеется ли между зависимостями взаимосвязь показывает определенную зависимость между переменными, а именно: в среднем, чем больше жилая площадь, тем выше отпускная цена. Применить к данным корреляционный анализ   Изучить теоретическую справку по КЭ Корреляция, или коэффициент корреляции является распространенной общей характеристикой двумерных данных в том же смысле, в каком среднее и стандартное отклонение являются важными характеристиками для анализа одномерного набора данных. Коэффициент корреляции характеризует «силу (тесноту)» линейнойзависимости между двумя переменными. Возможные значения коэффициента корреляции лежат в диапазоне от –1 до +1. Отрицательный знак коэффициента корреляции указывает на то, что с увеличением значений одной переменной значения другой переменной будут уменьшаться (прямая с отрицательным углом наклона). В случае положительного коэффициента корреляции с увеличением значений одной переменной значения другой переменной также увеличиваются (прямая с положительным углом наклона). Формула для вычисления выборочного коэффициента корреляции имеет вид: , где и – средние значения переменных X и Y; Sx и Sy – стандартные отклонения этих переменных. Числитель в приведенной формуле включает в себя сумму попарных произведений, которая выражает взаимодействие двух переменных X и Y. Знаменатель в формуле введен для нормирования числителя таким образом, чтобы коэффициент корреляции стал безразмерным, и его можно было легко интерпретировать числом в диапазоне от –1 до +1. Еще раз подчеркнем, что коэффициент корреляции характеризует только линейную зависимость. Если абсолютная величина коэффициента корреляции равна 1, то это указывает на идеальную (функциональную) линейную взаимосвязь. Если коэффициент корреляции равен 0, то это означает, что между переменными отсутствует линейная зависимость. В таком случае требуется дополнительный анализ, поскольку переменные либо являются независимыми, либо взаимосвязь между ними имеет нелинейный характер. Провести корреляционный анализ средствами Определить коэффициенты корреляции Корреляционный анализ может выполняться двумя способами: Инструментом Анализ данных Мастером функций КОРРЕЛ В отличие от инструмента анализа Корреляция статистическая функция КОРРЕЛ не статична, т.е. при изменении данных в исходном диапазоне значение коэффициента корреляции, рассчитанного с помощью функции КОРРЕЛ, тоже изменится. Запустить режим Анализ данных Инструмент анализа: Корреляция Запустить Корреляционный анализ Выберите команду: Сервис®Анализ данных®Корреляция. Установить параметры корреляции В диалоговом окне Корреляция установите параметры как указано ниже на рисунке. Анализировать результат Результатом является матрица попарных корреляций. На диагонали расположены 1, показывающие, что каждая переменная положительно коррелированна сама с собой. Значение коэффициента корреляции (0, 814651) указано в левой нижней части матрицы в ячейке E4. Правая верхняя часть матрицы пустая, т.к. ее значения совпадают с соответствующими значениями в левой нижней части. Определить коэффициенты корреляции с помощьюМастер функций вызовите Мастер функций выберите статистическую функцию КОРРЕЛ   1. Выделите ячейку D7, 2. В диалоговом окне Аргументы функции щелкните в поле Массив1, а затем 3. выделите диапазон A2: A16, не включая метку. 4. Теперь щелкните в поле Массив2 и выделите диапазон B2: B16, 5. не включая метку. 6. Щелкните на кнопке ОК. Вычислите коэффициент корреляции, используя 7.. Для этого в ячейку D6 введите Функция КОРРЕЛ. Анализировать результат 1. Полученное значение коэффициента корреляции (0, 814651) близко к 1. 2. Это указывает на то, что между ценой на недвижимость и размером площади существует сильная положительная линейная взаимосвязь. Точки данных довольно плотно сгруппированы (с небольшим случайным отклонением) вокруг прямой, направленной вверх и вправо. Выполнит анализ Парная корреляция Попарные корреляции Инструмент анализа Корреляция особенно полезен при определении попарных корреляций трех и более переменных. Полученные результаты используются для анализа множественной регрессионной модели. Сформировать исходные данные В таблице 2 данные, которые приведены в таблице 1, дополнены еще одной переменной – оценкой. Таблица 2. Объекты недвижимости Объект       Объект       7, 8 26, 0 14, 6 37, 2 23, 8 31, 0 26, 0 38, 4 28, 0 37, 4 30, 0 43, 6 26, 2 34, 8 29, 2 44, 8 22, 4 39, 2 24, 2 40, 6 28, 2 38, 0 29, 4 41, 8 25, 8 39, 6 23, 6 45, 2 20, 8 31, 2
Запустить анализ	1. Выберите команду: Сервис®Анализ данных®Корреляция.
	2. В диалоговом окне Корреляция в поле Входной интервал укажите диапазон данных A1: C16, включая метки. 3. Проверьте, что данные сгруппированы по столбцам и установлен флажок Метки в первой строке. 4. В области Параметры вывода включите опцию Выходной интервал, 5. щелкните в текстовом поле и выделите ячейку E2, определяющую левый верхний угол области вывода результатов. 6. Щелкните на кнопке ОК.
	Интерпретация результатов Выходные данные представляют собой матрицу трех попарных корреляций. Наибольшая корреляция 0, 814651 – между Площадью и Ценой. Корреляция между Оценкой и Ценой 0, 67537 – меньше и означает меньшую линейную зависимость между этими двумя переменными. Наименьшая корреляция 0, 424219 – между Площадью и Оценкой. Если мы хотим в линейной регрессионной модели использовать для прогноза отпускной цены одну независимую переменную, то полученные парные корреляции показывают, что Площадь больше подходит, чем Оценка, т.к. коэффициент корреляции 0, 814651 больше, чем 0, 67537. Если же мы хотим во множественной линейной регрессионной модели использовать для прогноза отпускной цены две независимые переменные, то подойдут Площадь и Оценка, и не будет проблем с их взаимной коррелированностью, т.к. коэффициент корреляции (0, 424219) этих двух переменных мал.
Выполнить ковариационный анализ
Изучить теоретическую справку	Ковариация (корреляционный момент), также как и корреляция, является характеристикой степени линейной зависимости двух переменных. Выражением для вычисления ковариации является числитель в формуле для коэффициента корреляции, а это означает, что ковариация и корреляция представляют, в действительности, одну и ту же информацию. Однако значения ковариации сложнее интерпретировать, т.к. ее единицы измерения являются произведением единиц измерения каждой переменной. Например, для цен и жилой площади ковариация выражена в единицах квадратных метров, умноженных на тысячи долларов. Поэтому при анализе обычно предпочитают использовать коэффициент корреляции, не имеющий размерности. Тем не менее, в некоторых ситуациях ковариация используется как самостоятельная характеристика.
Сформировать исходные данные	Взять прежние
Применить Инструмент анализа: Ковариация	1. Откройте файл Двумерные данные.xls. 2. На Листе2 в ячейку D10 введите Инструмент анализа: Ковариация. 3. Выберите команду: Сервис®Анализ данных®Ковариация. 4. В диалоговом окне Ковариация установите параметры как указано ниже на рисунке. 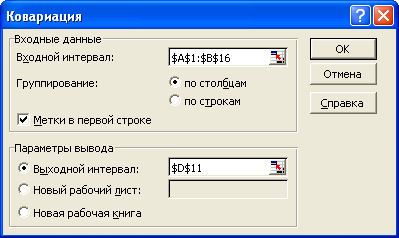Щелкните на кнопке ОК
Анализировать результаты	5. Результаты будут расположены в диапазоне D11: F13 (см. рисунок ниже). Результатом является матрица попарных ковариаций. На диагонали расположены дисперсии для каждой переменной (квадрат стандартного отклонения). Значение ковариации Цены и Площади (853, 2427) указано в левой нижней части матрицы в ячейке E13. Правая верхняя часть матрицы пустая, т.к. ее значения совпадают с соответствующими значениями в левой нижней части.
Выполнить ковариационный анализ с помощью мастер функций 1. Вычислите ковариацию, используя Мастер функций.	2. Для этого в ячейку D15 введите Функция КОВАР. 3. Выделите ячейку D16, 4. вызовите Мастер функций 5. выберите статистическую функцию КОВАР. 6. В диалоговом окне Аргументы функции 7. щелкните в поле Массив1, а затем 8. выделите диапазон A2: A16, не включая метку. 9. Теперь щелкните в поле Массив2 и выделите диапазон B2: B16, не включая метку. Щелкните на кнопке ОК. Замечание. В отличие от инструмента анализа Ковариация статистическая функция КОВАР не статична, т.е. при изменении данных в исходном диапазоне значение ковариации, рассчитанной с помощью функции КОВАР, тоже изменится.

Контрольные вопросы

1. В чем отличие анализа двумерных данных от анализа одномерных данных?

2. На какие вопросы можно ответить, проанализировав двумерные данные?

3. Что такое диаграмма рассеяния? С какой целью она используется для анализа?

4. Что такое коэффициент корреляции?

5. На что указывает знак (положительный или отрицательный) коэффициента корреляции?

6. Если большие значения X вызывают появление больших значений Y, то какой, по вашему мнению, должна быть корреляция – положительной, отрицательной или нулевой? Почему?

7. Для каждого из приведенных ниже равенств укажите типичный вариант интерпретации?

а) r = 1;

б) r = 0, 85;

в) r = 0;

г) r = –0, 15;

д) r = –1.

8. Поясните как, по вашему мнению, располагаются точки на диаграмме рассеяния в следующих ситуациях.

а) Взаимосвязь между X и Y отсутствует.

б) Линейная взаимосвязь с сильной положительной корреляцией.

в) Линейная взаимосвязь с сильной отрицательной корреляцией.

г) Линейная взаимосвязь со слабой положительной корреляцией.

д) Линейная взаимосвязь со слабой отрицательной корреляцией.

е) Линейная взаимосвязь с корреляцией +1?

ж) Линейная взаимосвязь с корреляцией –1?

9. Что представляет собой ковариация между X и Y?

10. Какую из характеристик легче интерпретировать – корреляцию или ковариацию? Почему?

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Популярное:

1. I. Данные лабораторных и инструментальных методов исследования.
2. II. НАУЧНОЕ РУКОВОДСТВО КУРСОВЫМИ РАБОТАМИ
3. IV. Внеурочная и внеклассная работа.
4. VI. Некоторые данные и предположения о сигнальном воздействии палеоантропов на диких животных
5. А. Импульс силы. Б. Момент силы. В. Работа силы. Г. Плечо силы. Д. Проекция силы.
6. Безопасность движения поездов при путевых работах
7. В. Методы, дающие косвенные визуальные данные звучащей речи
8. Внеклассная работа по естествознанию
9. Внеурочная работа по естествознанию
10. Воспитательная работа с осужденными к лишению свободы.
11. Воспитательно-коррекционная работа с подростками во внеурочной работе
12. Все данные взяты из Cancer Facts and Figures- 1996, стр. 1. Также California Cancer Facts and Figures - 1997, стр. 3.