Формулы ДПФ для вещественного сигнала.
Пусть рассматривается сигнал  ,
,  . По
. По  отсчетам
отсчетам  можно найти
можно найти  значений коэффициентов
значений коэффициентов  ,
,  , в том числе
, в том числе  значений
значений  и
и  значений
значений 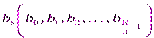 . Эти коэффициенты определяют среднее значение сигнала
. Эти коэффициенты определяют среднее значение сигнала 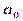 и
и 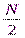 гармоник сигнала,
гармоник сигнала,  . Поэтому в ДПФ получается только отрезок ряда Фурье, который в размерных переменных имеет вид
. Поэтому в ДПФ получается только отрезок ряда Фурье, который в размерных переменных имеет вид
или

| (2.11)
|
Это обратное ДПФ. Прямое ДПФ определено формулами для коэффициентов  ,
,  при переходе от интегралов к суммам
при переходе от интегралов к суммам
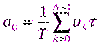 , ,
| (2.12)
|
 , ,
| (2.13)
|
 . .
| (2.14)
|
В безразмерном виде основные формулы ДПФ имеют вид:

| (2.15)
|
или

| (2.16)
|
Формула (2.15) позволяет восстанавливать форму сигнала по его известному спектру и поэтому ее называют обратным ДПФ. Если же сигнал задан, т.е. известен массив  и нужно определить его спектр, то применяется прямое ДПФ. Оно дает синусные и косинусные коэффициенты в (2.15) путем суммирования всех отсчетов сигнала.
и нужно определить его спектр, то применяется прямое ДПФ. Оно дает синусные и косинусные коэффициенты в (2.15) путем суммирования всех отсчетов сигнала.

| (2.17)
|

| (2.18)
|
Эти формулы применимы для гармоник с номерами  , а для нулевой гармоники (
, а для нулевой гармоники (  ) и последней
) и последней  в них нужно заменить коэффициент
в них нужно заменить коэффициент  на
на  . Из (2.18) следует, что
. Из (2.18) следует, что  и
и  произвольные, т.к.
произвольные, т.к.  Из (2.17) для нулевой и последней гармоник получаем
Из (2.17) для нулевой и последней гармоник получаем
 , ,
| (11.19)
|

| (11.20)
|
Из (2.19) следует, что коэффициент  определяет средний уровень сигнала на периоде, т.е. амплитуду постоянной составляющей
определяет средний уровень сигнала на периоде, т.е. амплитуду постоянной составляющей  .
.
Формулы (2.17), (2.18) можно пояснить также следующим образом. Суммирование произведений в них означает проверку ортогональности сигнала и гармонического колебания определенной частоты. Их ортогональность, соответствующая нулевым или малым коэффициентам  и
и  означает, что они непохожи, т.е. таких колебаний нет в сигнале.
означает, что они непохожи, т.е. таких колебаний нет в сигнале.
Сравнение ДПФ и АПФ
АПФ – это аналоговое преобразование Фурье. Оно определяет коэффициенты Фурье для аналогового сигнала, т.е. для непрерывной функции  . Его формулы записаны в выше. Здесь укажем лишь на различия формул ДПФ и АПФ для периодического сигнала.
. Его формулы записаны в выше. Здесь укажем лишь на различия формул ДПФ и АПФ для периодического сигнала.
В (2.15), (2.16) суммируется конечное количество гармоник, а в АПФ их количество может быть бесконечным.
В (2.17), (2.18), (2.19), (2.20) при вычислении коэффициентов используются суммы, а в АПФ – интегралы, т.е. рассматривается бесконечно большое количество отсчетов на периоде.
С помощью интегралов в АПФ могут быть легко вычислены спектры лишь нескольких простых сигналов, а основное достоинство ДПФ – это возможность вычисления спектров любых дискретных сигналов.
Периодичность спектра.
Выше указывалось, что ДПФ дает гармоники с номерами от  до
до  . Что будет, если вычислить гармонику с номером
. Что будет, если вычислить гармонику с номером  ?
?
Пусть  , т.е.
, т.е.  . Используем (2.17) получим
. Используем (2.17) получим
 , ,
| (2.21)
|
т.к.  .
.
Получили
 , ,
| (2.22)
|
Аналогичным образом получим
 , ,
| (2.23)
|
Эти формулы означают, что спектр ДПФ периодический по  , т.к.
, т.к.  . Кроме того, относительно имеется симметрия для
. Кроме того, относительно имеется симметрия для  и антисимметрия для
и антисимметрия для  .
.
Следовательно, если амплитудный спектр известен для гармоник  , то далее все повторяется и поэтому вычисления при
, то далее все повторяется и поэтому вычисления при  никогда не проводятся, см.рис.2.3.
никогда не проводятся, см.рис.2.3.

|
| Рис.2.3. Периодичность спектра ДПФ.
|
Отметим, что с помощью ДПФ (при  ) правильно вычисляется половинка любой " шапочки" рис.2.3, что используется при вычислении спектров модулированных сигналов, например, для
) правильно вычисляется половинка любой " шапочки" рис.2.3, что используется при вычислении спектров модулированных сигналов, например, для  .
.
Применение ДПФ для интерполяции и аппроксимации
Если задан дискретный периодический сигнал  , то прямое ДПФ (2.15) можно использовать для его интерполяции, т.е. для определения значений
, то прямое ДПФ (2.15) можно использовать для его интерполяции, т.е. для определения значений  для любых вещественных
для любых вещественных  , а не только для
, а не только для 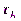 . При этом по аналогии со сплайном сначала должны быть вычислены все коэффициенты
. При этом по аналогии со сплайном сначала должны быть вычислены все коэффициенты  ,
,  , а затем выполнена интерполяция. Но этот способ мало эффективен из-за большого количества операций для вычислений функций sin, cos.
, а затем выполнена интерполяция. Но этот способ мало эффективен из-за большого количества операций для вычислений функций sin, cos.
Полученная непрерывная функция  будет точно проходить через заданные точки, соответствующие целым значениям
будет точно проходить через заданные точки, соответствующие целым значениям  . Но если при вычислении суммы в (2.15) часть гармоник отбросить, то получим аппроксимацию, т.е. непрерывная функция
. Но если при вычислении суммы в (2.15) часть гармоник отбросить, то получим аппроксимацию, т.е. непрерывная функция  будет близка к исходным точкам. Это позволяет, например, устранять шумы или помехи в сигналах.
будет близка к исходным точкам. Это позволяет, например, устранять шумы или помехи в сигналах.
ЭФФЕКТ НАЛОЖЕНИЯ ЧАСТОТ И КОМПЛЕКСНАЯ ФОРМА ДПФ.
Наложение частот в ДПФ.
Этот эффект проявляется в тех случаях, когда количество отсчетов  сигнала на периоде выбрано недостаточно большим.
сигнала на периоде выбрано недостаточно большим.
Рассмотрим произвольный аналоговый сигнал  . Пусть
. Пусть  - его амплитудный спектр, который в общем случае содержит бесконечное количество гармоник. Пусть рассматриваемый сигнал дискретизирован и по
- его амплитудный спектр, который в общем случае содержит бесконечное количество гармоник. Пусть рассматриваемый сигнал дискретизирован и по  его точкам с помощью ДПФ вычислен спектр
его точкам с помощью ДПФ вычислен спектр  , содержащий
, содержащий  гармоник.
гармоник.
Если значение N выбрано правильно, то спектры  и
и  совпадают. Если же
совпадают. Если же  недостаточно велико, то спектры
недостаточно велико, то спектры  и
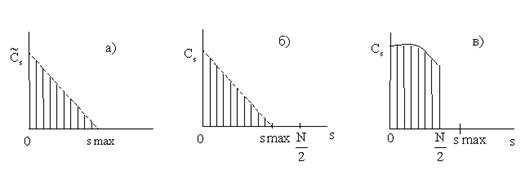
и  существенно различаются, что показано на рис.2.4.
существенно различаются, что показано на рис.2.4.
|
Рис. 2.4. Спектры аналогового и дискретного сигнала при правильном (б) и неправильном (в) выборе значения  . .
|
На рис.2.4в даны только гармоники для рабочего диапазона ДПФ  , а далее эти гармоники повторяются в соответствии с рис.2.3. Большие погрешности в спектре рис.2.1в обусловлены тем, что в исходном аналоговом сигнале есть гармоники с номерами
, а далее эти гармоники повторяются в соответствии с рис.2.3. Большие погрешности в спектре рис.2.1в обусловлены тем, что в исходном аналоговом сигнале есть гармоники с номерами  , а в ДПФ они не рассматриваются из-за периодичности спектра.
, а в ДПФ они не рассматриваются из-за периодичности спектра.
Пусть  - отсчет исходного аналогового сигнала
- отсчет исходного аналогового сигнала  , т.е.
, т.е.  ,
,  .
.
Далее знак суммы по  будет означать суммирование по этим значением
будет означать суммирование по этим значением  , т.е. по всем отсчетам. Используем целый индекс
, т.е. по всем отсчетам. Используем целый индекс  для гармоник аналогового сигнала,
для гармоник аналогового сигнала,  в общем случае. Тогда аналоговое преобразование Фурье (АПФ) можно записать в соответствии с (2.2) в виде
в общем случае. Тогда аналоговое преобразование Фурье (АПФ) можно записать в соответствии с (2.2) в виде

| (2.24)
|
По отсчетам (2.24) вычисляем прямое ДПФ, т.е. подставляем (2.24) в (2.17) или (2.19). Получим двойную сумму вида
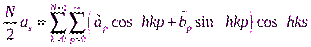
| (2.25)
|
Раскроем скобки и используем известные формулы для произведений, например,

Можно показать, что

При этом учитывается, что 
 . Поэтому для коэффициента
. Поэтому для коэффициента  (или
(или  ) большинство слагаемых в двойной сумме (2.25) по k и p будет равно нулю и останутся только слагаемые с
) большинство слагаемых в двойной сумме (2.25) по k и p будет равно нулю и останутся только слагаемые с  и слагаемые, для которых
и слагаемые, для которых  кратно
кратно  .
.
Если аккуратно провести все указанные преобразования, то из (2.25) получим

| (2.26)
|
и аналогичную формулу для  . Из (2.26) делаем следующие выводы:
. Из (2.26) делаем следующие выводы:
1. В вещественном ДПФ вычисляются гармоники с номерами  , хотя в исходном аналоговом сигнале могут присутствовать гармоники с номерами
, хотя в исходном аналоговом сигнале могут присутствовать гармоники с номерами  .
.
2. Если в спектре исходного аналогового сигнала есть гармоники с номерами  то при вычислении ДПФ они накладываются на гармоники с номерами
то при вычислении ДПФ они накладываются на гармоники с номерами  и искажают их. Наложение происходит для гармоник с номерами
и искажают их. Наложение происходит для гармоник с номерами  и
и  , если
, если  кратно
кратно  . Это и есть эффект наложения частот (см. рис.2.5). При этом исходный спектр складывается как бы " гармошкой".
. Это и есть эффект наложения частот (см. рис.2.5). При этом исходный спектр складывается как бы " гармошкой".

|
Рис.2.5. Эффект наложения частот при ДПФ.  - амплитудный спектр аналогового сигнала; здесь для ДПФ - амплитудный спектр аналогового сигнала; здесь для ДПФ  , т.к. , т.к.  . .
|
3. Для устранения эффекта наложения частот нужны фильтры верхних частот для аналогового сигнала или большие значения N, т.к. спектр аналогового сигнала не должен иметь гармоник с номерами  . Если такие гармоники есть, то они не должны превышать заданной погрешности вычисления спектра.
. Если такие гармоники есть, то они не должны превышать заданной погрешности вычисления спектра.
Пример. Пусть в аналоговом сигнале имеем  ,
,  ,
,  ,
,  , выбрано
, выбрано  . Это ошибка, т.к. при ДПФ гармоники 50 и 49 накладываются на нулевую и первую соответственно, что даст погрешность 20%. Нужно выбрать
. Это ошибка, т.к. при ДПФ гармоники 50 и 49 накладываются на нулевую и первую соответственно, что даст погрешность 20%. Нужно выбрать  .
.
2.10. Теорема отсчетов.
Другое название теоремы – теорема Котельникова, которое используется в отечественной литературе. Пусть исходный сигнал имеет спектр, ограниченный частотой  , которая соответствует номеру гармоники
, которая соответствует номеру гармоники  , где
, где  – период сигнала.
– период сигнала.
При дискретизации должно выполняться условие
 , ,
| (2.27)
|
т.е. отсчетов должно быть не меньше удвоенного количества гармоник.
Условие (2.27) можно записать в обычной для ДПФ форме
 , ,
| (2.28)
|
которая использовалась выше.
Формулы (2.27) и (2.28) – это теорема отсчетов в безразмерных переменных. Используя размерные переменные  ,
,  ,
,  (см. раздел 13.3) и частоту дискретизации
(см. раздел 13.3) и частоту дискретизации  эти формулы можно записать в более известном виде
эти формулы можно записать в более известном виде
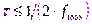 , ,
| (2.29)
|
или  .
.
Пример телевизионного сигнала
Спектр телевизионного радиосигнала имеет полосу 8 МГц от  МГц до
МГц до  МГц. Здесь
МГц. Здесь  – несущая частота конкретного канала. Пусть
– несущая частота конкретного канала. Пусть  МГц. Получаем
МГц. Получаем  МГц. За период выберем длительность одной строки
МГц. За период выберем длительность одной строки  мксек, т.е. основная частота
мксек, т.е. основная частота  МГц.
МГц.
При дискретизации высокочастотного сигнала по (12.4)
 на периоде, что соответствует частоте дискретизации
на периоде, что соответствует частоте дискретизации  МГц.
МГц.
Это нереальная частота дискретизации. Если же радиосигнал демодулировать и перенести спектр в диапазон от 0 до 8 МГц, то получим значение 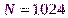 и
и  МГц, реализуемые в современной цифровой обработке.
МГц, реализуемые в современной цифровой обработке.
Контроль точности.
Если спектр сигнала неизвестен, то использовать (2.27) для выбора  нельзя. В этом случае выбирается произвольное
нельзя. В этом случае выбирается произвольное  и определяется
и определяется  гармоник. Затем шаг дискретизации
гармоник. Затем шаг дискретизации  уменьшается в 2 раза и ДПФ вычисляют по
уменьшается в 2 раза и ДПФ вычисляют по  точкам, что дает
точкам, что дает  гармоник. Можно также выполнить контроль, взяв точки через одну, т.е. по
гармоник. Можно также выполнить контроль, взяв точки через одну, т.е. по  отсчетам сигнала.
отсчетам сигнала.
Сравнивая амплитуды гармоник с одинаковыми номерами s в двух расчетах, получим погрешности вычислений по аналогии с (2.26). Если погрешность больше допустимой, то значения  должны быть увеличены, т.е. следует использовать значения
должны быть увеличены, т.е. следует использовать значения  и
и  , например.
, например.
Популярное:

