Модели с ограниченными зависимыми переменными

⇐ ПредыдущаяСтр 7 из 16Следующая ⇒

В практике социально-экономических исследований на микро-уровне достаточно часто возникают ситуации, когда зависимая переменная является количественной и непрерывной, т. е. удовлетворяет предпосылкам классической модели, но выборка подвергается усечению или цензурированию.

Усечение имеет место, когда данные выбираются из некоторого большего по объему подмножества данных (наблюдений), например, в исследовании доходов рассматриваются семьи с доходами ниже или выше определенного уровня (скажем, черты бедности).

Вместо усечения выборок может применяться также их цензурирование. В частности, в исследованиях доходов рассматривается вся выборка, но принимается, что у семей с доходами выше или ниже определенного уровня доходы находятся на этом же уровне. Следствием цензурирования и усечения выборок является искажение значений выборочных параметров распределений, в частности, их математических ожиданий и дисперсий. Соответственно выводы, полученные на основании усеченных и цензурированных выборок, следует очень осторожно распространять на генеральную совокупность.

Модели усеченных выборок

Предположим, усеченное распределение является частью неусеченного распределения, которая находится выше или ниже определенного порогового значения.

Плотность непрерывной случайной переменной z, усеченной выше уровня b, определяется согласно следующему выражению:

Выражение (10.136) вытекает, из формулы условной вероятности. В самом деле, условная вероятность того, что случайная величина z примет некоторое значение при условии, что z< b, определяется следующим образом:

ò ò /ò

Продифференцировав левую и правую части выражения (10.137) по z, получим (10.136).

Во многих практических исследованиях предполагается, что случайная величина z распределена по нормальному закону. В этом случае вероятность того, что z> b определяется согласно следующему выражению:

где m и s – соответственно математическое ожидание и стандартное отклонение случайной величины z; b=(b–m)/s; Ф(.) – значение стандартной нормальной интегральной функции распределения в соответствующей точке.

Тогда согласно выражению (10.136), функция плотности усеченного нормального распределения определяется как:

где j(.) – стандартная нормальная функция распределения.

На рис. 10.6 представлены графики функций плотностей усеченного стандартного нормального распределения с m=0 и s=1 для b=–0, 5; 0; 0, 5. Из графиков, представленных на этом рисунке следует, что усечение как бы “поднимает” функцию плотности на оставшемся после усечения участке над графиком этой функции “неусеченного” распределения.

В дальнейшем случайную переменную с усеченным распределением будем называть усеченной случайной переменной.

Заметим, что математическое ожидание и дисперсия усеченной случайной переменной определяются согласно следующим выражениям:

M[z|z> b]=ò

D[z|z> b]=ò

Проведя интегрирование в выражениях (10.140)–(10.141) с учетом того, что функция плотности f(z, z> b) определена выражением (10.139), получим, что математическое ожидание и дисперсия усеченной случайной переменной z соответственно равны:

M[z|при усечении]=m+s× l(b). (10.142)

D[z|при усечении]=s²× [1–d(b)]. (10.143)

где b=(b–m)/s;

l(b)=j(b)/[1–F(b)], если z> b; (10.144)

l(b)=–j(b)/F(b), если z< b; (10.145)

d(b)=l(b)× [l(b)–b]. (10.146)

Указатель усечения

Среднее значение

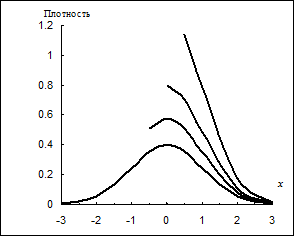
Рис. 10.6. Зависимости плотностей усеченного нормального распределения от степени усечения

Функцию l(b) называют обратным отношением Миллса или функцией отказов (hazard-function), b – степенью усечения.

Заметим, что d(b)< 1 при любом значении b.

Из выражения (10.142) следует, что математическое ожидание усеченной стандартной нормальной переменной является функцией от степени усечения (см. рис. 10.7).

Рассмотрим некоторые результаты, приведенные на рис. 10.7. В частности, математическое ожидание стандартной нормальной величины при усечении z³ 0 равно 0, 79, а при усечении z£ b равно –0, 79.

Несложно также убедиться, что вероятность того, что х меньше b, является возрастающей функцией от b. С возрастанием этой вероятности увеличивается количество нерассматриваемых элементов совокупности, а, следовательно, возрастает и математическое ожидание усеченной случайной переменной.

0, 79

–0, 79

M[z|z£ b]

M[z|z³ b]

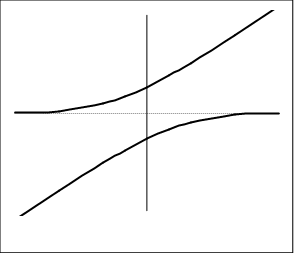
Рис. 10.7. Графики зависимости математических ожиданий стандартной нормальной величины от степени усечения

На рис. 10.8 приведена функция, отражающая взаимосвязь между математическим ожиданием M[z|z> b] и вероятностью Р[z> b] для стандартного нормального распределения.

P[z> b]

P[z> b]=0Þ b®+¥ P[z< b]=1Þ b®–¥

M[z|z³ b]

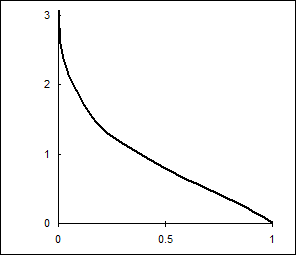
Рис.10.8. Условное среднее как функция степени усечения.

Предположим, что зависимость некоторой случайной переменной y_t, от значений влияющих на нее факторов, можно представить следующим образом:

y_t = a ¢ × x _t +e_t, (10.148)

где x _t – вектор независимых переменных, влияющих на переменную y_t; a – вектор параметров; e_t– ошибка модели, в отношении которой предполагается, что она распределена по стандартному нормальному закону с нулевым математическим ожиданием и постоянной дисперсией, e_t ~N[0, s²].

Переменная y_t, описанная выражением (10.148), распределена по нормальному закону с математическим ожиданием m_t= a ¢ × x _t и дисперсией s².

Рассмотрим распределение зависимой переменной y_tпри условии, что наблюдаемые значения y_tпревышают некоторый порог b. Согласно выражению (10.142) получим, что условное математическое ожидание y_tдля модели (10.148) является нелинейной функцией от х _t и a, и определяется как

M[y_t | y_t > b]= a ¢ × x _t +

Перепишем выражение (10.149) с использованием функции отказов l(b_t) (см. выражение (10.144)):

M[y_t | y_t > b]= a ¢ × x _t +s× l(b_t), (10.150)

где b_t =(b – a ¢ × x _t)/s.

С учетом вида выражения (10.150) оценим величину маржинального эффекта факторов x _tдля случая усеченной выборки:

Поскольку для каждого набора факторов x _t выполняется соотношение 0< d(b_t)< 1, то из выражения (10.151) вытекает, что для любого x_it(i=1, 2,..., n; t=1, 2,..., T) маржинальный эффект меньше соответствующего коэффициента a _i.

Заметим, что в силу специфики выражения (10.150) ошибка e_t модели (10.146), построенной для усеченной выборки, имеет математическое ожидание s× l(b_t). Дисперсия ошибки e_tв этом случае определяется следующим образом:

D[e_t | y_t > b]=s²× [1–d(b_t)]. (10.152)

где s²– дисперсия ошибки модели (10.148), построенной на неусеченной выборке; d(b_t)=l(b_t)× [l(b_t)–b_t]; l(b_t)=j(b_t)/[1–F(b_t)]; b_t =(b – a ¢ × x _t)/s.

Таким образом, из выражений (10.150) и (10.152) вытекает, что оценки параметров модели (10.148), определенные на основании усеченной выборки зависимой переменной (y_t> b или y_t< b), являются смещенными и несостоятельными по сравнению с оценками, которые могли бы быть получены по полной выборке.

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒