Модели прогнозирования физических процессов

Модели прогнозирования физических процессов

Физические процессы и их характеристики

Классификация физических процессов

Все наблюдаемые процессы, характеризующие физические явления и изменения состояний объектов, можно классифицировать в самом общем виде как детерминированные и недетерминированные. К детерминированным относятся процессы, которые могут быть описаны точными математическими соотношениями. Рассмотрим, например, твердое тело, подвешенное на упругой пружине (рис. 5.1, а).

Пусть m – масса тела, а k – коэффициент жесткости пружины. Предположим, что тело получает начальное смещение X_m из положения равновесия (рис. 5.1, б) и освобождается в момент времени t = 0. На основе фундаментальных законов механики или с помощью повторных наблюдений можно установить справедливость следующего соотношения:

. (5.1)

Формула (5.1) достаточно точно описывает положение тела в любой момент времени в недалеком будущем. Для более точного предсказания положения тела в течение длительного времени требуется учесть затухание колебаний. Следовательно, физический процесс, характеризующий движение данного тела, относится к детерминированным.

На практике встречается много физических процессов, которые с высокой точностью могут быть описаны математическими соотношениями. Например, движение спутника по околоземной орбите, изменение напряжения на конденсаторе, который разряжается через сопротивление, вибрация несбалансированного ротора генератора или изменение температуры воды при охлаждении. Детерминированные процессы можно классифицировать, как показано на рис. 5.2.

Рис. 5.1. Тело, подвешенное на пружине

Рис. 5.2. Классификация детерминированных процессов

Существует много процессов, имеющих недетерминированный, т. е. случайный характер. Например, изменение уровня сигнала в канале связи, температура воздуха, мощность, потребляемая из сети в заводском цехе. Точное значение такого процесса в некоторый момент времени в будущем предсказать невозможно. Эти процессы случайны по своей природе и должны описываться не точными уравнениями, а при помощи осредненных статистических характеристик. Будем обозначать случайный процесс x(t) случайной функцией от независимой переменной t.

Случайные процессы можно классифицировать, как показано на рис. 5.3.

Рис. 5.3. Классификация случайных процессов

Во многих случаях трудно решить, относится рассматриваемый физический процесс к детерминированным или случайным. Можно, например, считать, что в действительности ни один физический процесс не является строго детерминированным, поскольку всегда существует возможность того, что в будущем какое-либо непредвиденное событие изменит течение процесса таким образом, что полученные данные будут носить характер иной, чем предполагалось ранее. С другой стороны, можно утверждать, что в действительности ни один физический процесс не имеет строго случайной природы, так как если достаточно хорошо знать механизм изучаемого процесса, его можно описать точными математическими соотношениями.

Практически решение о детерминированном или случайном характере процесса принимается исходя из возможности либо невозможности воспроизведения его при заданных условиях. Если многократное повторение опыта дает одинаковые результаты (с точностью до ошибки измерения), то можно, вообще говоря, считать процесс детерминированным. Если же повторение опыта в идентичных условиях приводит к разным исходам, то природа процесса полагается случайной.

Детерминированные процессы

Детерминированные периодические процессы подразделяются на гармонические и полигармонические. Гармоническими называют процессы, которые могут быть описаны функцией

(5.2)

где X_m – амплитуда;

f₀ – циклическая частота, измеряемая в циклах в единицу времени;

q – начальная фаза, рад.

Соотношение (5.2) может быть представлено графически в функции времени и в амплитудно-частотном изображении (спектре), как показано на рис. 5.4.

Рис. 5.4. Гармонический процесс и его спектр

Циклическая частота , где T – период гармонических колебаний.

Полигармонические процессы описываются функцией времени, точно повторяющей свои значения через одинаковые интервалы:

(5.3)

Число циклов в единицу времени называется основной частотой f₁.

Полигармонический процесс может быть представлен рядом Фурье

(5.4)

где ;

Возможен и другой способ записи ряда Фурье для полигармонического процесса:

(5.5)

где

Как видно из (5.5), полигармонические процессы состоят из постоянной составляющей X₀ и бесконечного числа синусоидальных составляющих, называемых гармониками, с амплитудами X_i и начальными фазами q_i. Частоты всех гармоник кратны основной частоте f₁.

Полигармонический процесс может имеет вид, показанный на рис. 5.5, а, и соответствующий формуле (5.5) дискретный спектр, показанный на рис. 5.5, б.

Рис. 5.5. Полигармонический процесс и его спектр

В других случаях составляющая с основной частотой может отсутствовать. Предположим, например, что периодический процесс формируется в результате сложения трех синусоидальных функций с частотами 60, 75 и 100 Гц. Наибольший общий делитель этих чисел равен 5 Гц, поэтому период результирующего периодического процесса составляет 0, 2 с. Следовательно, при разложении в ряд Фурье значения X_i будут равны нулю при всех i, кроме i = 12, i = 15, i = 20.

Физические процессы полигармонического типа встречаются гораздо чаще простых гармонических процессов. В действительности, когда тот или иной процесс относят к типу гармонических, то зачастую при этом имеют в виду только приближенное представление процесса, который на самом деле является полигармоническим. Например, напряжение на выходе генератора переменного тока содержит небольшие колебания с частотами высших гармоник.

Однако процессы, образованные при суммировании двух или более гармонических функций с произвольными частотами, не будут, вообще говоря, периодическими. Сумма двух или более синусоидальных функций образует периодический процесс только в том случае, если отношение всех возможных пар частот представляет собой рациональные числа. Это означает, что существует некоторый основной период, удовлетворяющий формуле (5.3). Так, процесс

(5.6)

является периодическим, поскольку 2/3, 3/7 и 2/7 – рациональные числа (с основным периодом, равным единице). С другой стороны, процесс

(5.7)

не является периодическим, поскольку числа иррациональные и основной период равен бесконечности. В этом случае процесс является почти периодическим, но соотношение (5.3) не удовлетворяется при любых конечных значениях T.

Таким образом, к почти периодическим относятся такие процессы, которые могут быть описаны функцией времени:

, (5.8)

имеющей хотя бы одно отношение f_i/ f_j, которое не является рациональным числом.

Дискретный спектр почти периодического процесса аналогичен спектру полигармонического процесса.

К переходным относятся все непериодические процессы, не являющиеся почти периодическими процессами, описанными выше. Другими словами, переходные процессы включают в себя все не рассмотренные ранее процессы, которые могут быть описаны подходящими функциями времени. Три примера распространенных переходных процессов приведены на рис. 5.6.

Рис. 5.6. Примеры переходных процессов

Физические переходные процессы весьма многочисленны и разнообразны. Например, процесс, изображенный на рис. 5.6, а, может описывать изменение во времени температуры проводника после отключения протекавшего по нему тока. Кривая на рис. 5.6, б может характеризовать свободные колебания инерционной механической системы после прекращения действия вынуждающей силы. График

а б в

Рис. 5.7. Спектры переходных процессов

на рис. 5.6, в может описывать изменение во времени механического напряжения в тросе, который подвешен на опорах линии электропередачи и разрывается в момент c.

Важное отличие переходных процессов от периодических и почти периодических состоит в том, что их невозможно представить с помощью дискретного спектра. Однако в большинстве случаев получают непрерывное спектральное представление переходных процессов, используя интеграл Фурье

Спектр Фурье X(f) в общем случае является комплексной функцией, которая может быть записана в показательной форме:

. (5.9)

Здесь - модуль, а q(f) – аргумент. Модули преобразования Фурье трех переходных процессов, изображенных на рис. 5.6, показаны на рис. 5.7.

Случайные процессы

Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной. Случайные функции времени называют случайными процессами.

Реализацией случайной функции X(t) (выборочной функцией) называется конкретный вид, который она принимает в результате опыта. Реализация случайного процесса может рассматриваться как элемент множества возможных физических реализаций случайного процесса (рис. 5.8). Совокупность реализаций случайного процесса называется ансамблем реализаций. Совокупность значений реализаций в фиксированный момент времени (выборка случайных значений) называется сечением случайного процесса.

Рис. 5.8. Реализации случайного процесса

В любом сечении случайный процесс есть случайная величина.

Математическое ожидание случайного процесса есть функция времени

(5.10)

Второй центральный момент для двух сечений случайного процесса называется ковариационной функцией

(5.11)

где – центрированный случайный процесс.

При t = t′ ковариационная функция равна дисперсии случайного процесса

(5.12)

Математическое ожидание и ковариационная функция случайного процесса могут быть найдены по реализациям случайного процесса – осреднением по реализациям:

(5.13)

где N – число реализаций случайного процесса.

Если математическое ожидание и ковариационная функция не зависят от времени t, то процесс является стационарным:

(5.14)

где τ = t′ – t. В (5.14) ковариационная функция зависит только от величины τ, а не от места его расположения на оси времени (рис. 5.9).

Рис. 5.9. Время между двумя сечениями случайного процесса

Возможный вид ковариационной функции показан на рис. 5.10.

Во многих случаях используется нормированная ковариационная (или корреляционная) функция. Для стационарного случайного процесса

(5.15)

Величина корреляционной функции |r_X(t)| ≤ 1.

Возможно осреднение по времени отдельных выборочных функций (реализаций). Для k-й выборочной функции имеем:

(5.16)

Рис.5.10. Ковариационная функция случайного процесса

Если случайный процесс X(t) стационарен и характеристики m_X и R_X(τ ) одинаковы для различных выборочных функций, то такой процесс называют эргодическим.

Эргодические процессы представляют важный класс случайных процессов.

Нестационарными случайными процессами являются все случайные процессы, не обладающие свойствами стационарности. Эти процессы сложны в исследованиях, и зачастую в задачах по анализу их разбивают на интервалы стационарности или приближенно аппроксимируют стационарными процессами.

Анализ временных рядов

Графики нагрузки в ЭЭС являются последовательностями наблюдений или расчетных значений, показывающих изменения мощности в течение определенного периода времени. В суточных, недельных и годовых графиках отображается периодичность процесса изменения мощности нагрузки, связанная с режимом работы людей, сменой дня и ночи, недельными циклами и сезонными изменениями в течение года.

Суточные графики дней недели в общем повторяются изо дня в день с небольшими случайными различиями и режимами выходных и праздничных дней. Средний рост или снижение нагрузки в течение недели или нескольких недель связан с сезонными изменениями, в особенности в осенний и весенний периоды. Такие изменения, происходящие в среднем, относят к трендовым (непериодическим) составляющим графика нагрузки. Эти изменения для годовых графиков обусловлены естественным ростом нагрузки потребителей.

Суточные, недельные и годовые графики нагрузки часто прогнози-руют посредством разделения их на трендовую, периодическую и случайную составляющие:

(5.58)

где Q(t) – тренд – устойчивые систематические изменения;

S(t) – периодическая составляющая – колебания относительно тренда;

U(t) – нерегулярная составляющая – случайный шум.

Подобный подход справедлив, если принять гипотезу о том, что резких изменений во временном ряду не произойдет.

Пусть имеется временной ряд значений месячных максимумов мощности нагрузки за несколько лет (рис. 5.21).

Рис. 5.21. Ретроспектива временного ряда

Для выделения трендовой составляющей часто используют полиномиальную модель до третьего порядка включительно:

(5.59)

Иногда при выделении тренда предварительно применяют процедуру сглаживания, которая устраняет периодическую и случайную составляющие.

После вычитания из X(t) трендовой составляющей получается временной ряд, имеющий периодическую составляющую, которая вызвана суточными, недельными и сезонными периодами.

Рис. 5.22. Временной ряд без трендовой составляющей

Если имеется N результатов наблюдений за период T (N = 12 в годовом цикле, N = 7 – в недельном и N = 24 – в суточном), то периодическая модель процесса может быть представлена рядом Фурье

(5.60)

где n – количество частот, включенных в модель.

В общем случае наивысшая частота гармонического разложения дискретного ряда, называемая частотой Найквиста, определяется половиной интервала между наблюдениями, например при N = 12, n = 24.

– основная частота гармонического ряда.

Дисперсия, учитываемая i-й гармоникой:

(5.61)

Суммарная дисперсия . Как правило, первые три гармоники описывают до 90 % всей дисперсии.

Случайная составляющая

(5.62)

Для U(t) определяются статистические характеристики. Прогноз случайной составляющей ведется по одной из моделей прогноза случайного процесса. Сразу следует оценить интервал корреляции, и если прогноз ведется на время упреждения больше, чем интервал корреляции, то фактически по случайной составляющей оценивается лишь ошибка прогноза, так как после вычитания регулярных составляющих математическое ожидание процесса равно нулю.

Оценка коэффициентов моделей регулярных составляющих

Тренд

Оценка коэффициентов полиномиальной модели тренда может быть сделана разными способами:

1) с помощью функций Mathcad c : = regress( k, P, m) и Q_m(t): = in-terp( c, k, P, t). Здесь c – вектор коэффициентов, используемый функцией interp; k – вектор дискретных моментов времени, для которых заданы значения ретроспективы; P – вектор значений ретроспективы; m – порядок полинома (как 0, 1, 2 или 3); t – аргумент функции тренда. Можно также записать Q_m(t) = interp(regress( k, P, m), k, P, t);

2) как решение системы линейных уравнений по методу наименьших квадратов A = ( V ^T V )^–1 V ^T P. Функция тренда: . Здесь V – матрица, первый столбец которой состоит из единиц, второй – вектор k, третий вектор из элементов k в квадрате и т. д. V_{i, j} =
= k_ij_–1 ( i = 1…n, j = 1… m + 1), где n – количество данных ретроспективы.

Экспоненциальная модель тренда может быть получена с помощью функции expfit( k, P, vg ), которая возвращает вектор коэффициентов модели . Здесь вектор vg – начальные приближения для искомых коэффициентов модели.

Периодическая составляющая

Коэффициенты полигармонической составляющей процесса являются коэффициентами гармонического полинома вида (5.60). Вектор коэффициентов модели получается как решение системы линейных уравнений B = ( V ^T V ) ^–1 V ^T W. Здесь V – матрица из n строк и 2m столбцов; n – количество данных ретроспективы; m – количество частот, включенных в модель. Каждая последовательная пара столбцов матрицы V соответствует одной частоте и состоит из коэффициентов, вычисляемых как функции косинуса и синуса из выражения (5.60):

(5.63)

W – вектор, полученный из P вычитанием трендовой составляющей.

Возможно моделирование периодической составляющей с помощью другого представления ряда Фурье:

, (5.64)

где искомыми параметрами являются .

Пример. Чтение данных из файла Retro.prn

Представим тренд постоянной функцией, равной среднему значению за 5 суток

544.5

545.5

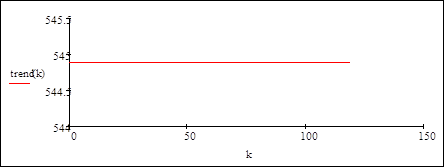
Остаточный временной ряд без тренда

–200

–100

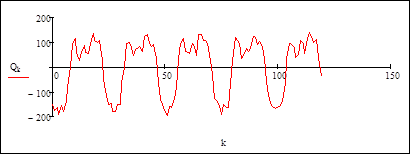
Моделирование периодической составляющей – 6 гармоник:

Графическое изображение периодической составляющей:

–100

–200

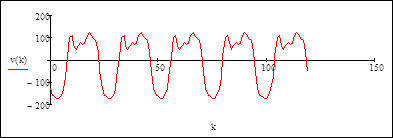
Остаточный временной ряд без тренда и периодической составляющей – случайная составляющая:

–20

–40

Определение статистических характеристик случайной составляющей временного ряда: среднее значение, медиана, среднеквадратическое отклонение:

Прогнозируемый график есть сумма тренда и случайной составляющей:

За ошибку прогноза принимаем среднеквадратическое отклонение случайной составляющей временного ряда:

Вопросы для самопроверки

1. Как подразделяются детерминированные физические процессы?

2. Как подразделяются случайные физические процессы?

3. Что такое прогноз?

4. Какие два вида переменных, зависящих от времени, выделяют при прогнозировании?

5. Как подразделяют прогноз по времени упреждения?

6. Дайте определение экспоненциальной модели прогнозирования.

7. В чем принципиальное различие логистической и экспоненциальной моделей прогнозирования?

8. Какие основные методы используют для прогнозирования случайных процессов?

9. Какие факторы влияют на прогноз суточных графиков нагрузки электроэнергетической системы?

10. В чем заключается прогноз графиков нагрузки методом анализа временных рядов?

Библиографический список

1. Лыкин А.В. Математическое моделирование электрических систем и их элементов: учеб. пособие. – Новосибирск: Изд-во НГТУ, 2003.

2. Неуймин Я.Г. Модели в науке и технике. История, теория, практика. – Л.: Наука, 1984.

3. Лыкин А.В. Mathcad в задачах электроэнергетики: учеб. пособие. –Новосибирск: Изд-во НГТУ, 1998.

4. Электрические системы. Математические задачи электроэнергетики. – М.: Высшая школа, 1981.

5. Лыкин А.В. Электрические системы и сети: учеб. пособие. – М.: Университетская книга; Логос, 2006.

6. Общая электротехника: учеб. пособие / Под ред. А.Т. Блажкина. – Л.: Энергоатомиздат, 1986.

7. Касаткин А.С., Немцов М.В. Электротехника: учеб. пособие. – М.: Энергоатомиздат, 1983.

8. Электротехника: учебник для вузов / Х.Э. Зайдель, В.В. Коген-Далин, В.В. Крымов и др. – М.: Высшая школа, 1985.

9. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи: учеб. пособие. – М.: Высш. шк., 1972.

10. Атабеков Г.И. Теоретические основы электротехники. Т. 1. Линейные электрические цепи: учебник для вузов. – М.: Энергия, 1978.

11. Совалов С.А. Режимы единой энергосистемы. – М.: Энергоатомиздат, 1983.

12. Жуков Л.А., Стратан И.П. Установившиеся режимы сложных электрических сетей и систем. Методы расчетов. – М.: Энергия, 1979.

13. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения. – М.: Наука, 1967.

14. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов / Пер. с англ. – М.: Мир, 1971.

15. Кадомская К.П. Основы теории случайных процессов: учеб. пособие. – Новосибирск: Изд-во НГТУ, 1999.

16. Гурский Е.И. Теория вероятностей с элементами математической статистики. – М.: Высш. шк., 1971.

17. Исследование операций: В 2 т. Т. 2. Модели и приложения / Пер. с англ. – М.: Мир, 1981.

18. Гужов Н.П. Статистическое прогнозирование режимов электропотребления предприятиями: учеб. пособие / Новосиб. электротехн. ин-т. – Новосибирск, 1992.

19. Использование методов теории подобия в прогнозировании выработки электроэнергии / Ю.Н. Астахов, К.К. Зубанов, В.В. Кавченков, Т.Е. Пашенкова // Электричество, 1973. – № 3. – С. 13 – 21.

20. Ефимов А.Н. Предсказание случайных процессов. – М.: 1976.

21. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. – М.: Мир, 1974.

22. Электрические системы. Режимы работы электрических систем и сетей / Под ред. В.А. Веникова. – М.: Высш. шк., 1975.

Приложение 1

Глоссарий*

Автоматическое регулирование напряжения и реактивной мощности – автоматическое поддержание требуемых значений напряжения и реактивной мощности путем воздействия на возбуждение синхронных электрических машин (синхронные и асинхронизированные генераторы, синхронные компенсаторы, синхронные двигатели) и других источников реактивной мощности (статические тиристорные компенсаторы, конденсаторные батареи), а также путем автоматического изменения коэффициентов трансформации трансформаторов и автотрансформаторов.

Ветвь электрической цепи – участок электрической цепи, по которому протекает один и тот же электрический ток.

Волна бегущая электромагнитная – электромагнитная волна, распространяющаяся в однородной среде (или в линии передачи) со скоростью, равной фазовой скорости в этой среде (или в линии).

Волна прямая (падающая) электромагнитная – электромагнитная волна, распространяющаяся в пространстве, в линии или в волноводе в направлении, принятом в системе отсчета за положительное направление.

Волновое сопротивление среды – отношение комплексной амплитуды напряженности электрического поля к комплексной амплитуде напряженности магнитного поля плоской бегущей синусоидальной электромагнитной волны, распространяющейся в данной среде.

Вращающееся магнитное поле – результирующее поле, создаваемое многофазной обмоткой электрической машины при протекании по ней многофазного переменного тока.

Главное сечение электрической цепи (графа электрической цепи) – сечение электрической цепи (графа электрической цепи), состоящее из ветвей связи и только одной ветви дерева графа электрической цепи.

Граф (электрической цепи) направленный – граф электрической цепи с указанием условно-положительных направлений электрических токов или напряжений в виде отрезков со стрелками.

Граф электрической цепи – графическое изображение электрической цепи, в котором ветви электрической цепи представлены отрезками, называемыми ветвями графа, а узлы электрической цепи – точками, называемыми узлами графа.

График электронагрузки (график нагрузки) – графическое (табличное) представление режимов потребления электроэнергии отдельными потребителями или энергосистемой в целом, отражающее изменение потребляемой мощности в течение суток, месяца или года.

Двигатель асинхронный – асинхронная машина, работающая в режиме двигателя.

Единая энергосистема – совокупность объединенных энергосистем, соединенных межсистемными связями, охватывающая значительную часть страны.

Контур графа электрической цепи – замкнутый путь, образованный узлами и ветвями графа электрической цепи, в котором один из узлов является одновременно начальным и конечным узлом пути графа электрической цепи.

Линия электропередачи (ЛЭП) – электроустановка, состоящая из проводов, кабелей, изолирующих элементов и несущих конструкций, предназначенная для передачи электрической энергии между двумя пунктами энергосистемы с возможным промежуточным отбором.

Линия электропередачи воздушная – устройство для передачи электроэнергии по проводам, расположенным на открытом воздухе и прикрепленным с помощью изоляторов и арматуры к опорам или кронштейнам и стойкам на инженерных сооружениях (мостах, путепроводах и т. п.).

Магнитное поле трансформатора – магнитное поле, созданное в трансформаторе совокупностью магнитодвижущих сил всех его обмоток и других частей, в которых протекает электрический ток.

Примечание. Для расчетов, определения параметров и проведения исследованний магнитное поле трансформатора мoжет быть условно разделено на взаимосвязанные части: оснoвное поле, поле рассеяния обмоток, поле токов нулевой последовательности и т. д.

Магнитный поток – скалярная величина, равная потоку магнитной индукции.

Максимум нагрузки энергосистемы – наибольшее значение активной нагрузки энергосистемы за определенный период времени.

Матрица инциденций – матрица, отражающая топологию электрической сети, например, матрица инциденций узловых ветвей, матрица инциденций контурных ветвей.

Матрица узловых проводимостей – матрица, описывающая зависимость между входными токами узлов и узловыми потенциалами.

Машина асинхронная – электромеханический преобразователь энергии, у которого частота вращения ротора не равна частоте вращения магнитного поля статора.

Машина синхронная – бесколлекторная машина переменного тока, у которой в установившемся режиме отношение частоты вращения ротора к частоте тока в цепи, подключенной к обмотке якоря, не зависит от нагрузки в области допустимых нагрузок.

Многополюсник – часть электрической цепи, имеющая более двух выделенных выводов.

Мощность комплексная (двухполюсника) – комплексная величина, равная произведению комплексного действующего значения синусоидального электрического напряжения и сопряженного комплекс-ного действующего значения синусоидального электрического тока двухполюсника.

Мощность потребляемая – общая мощность, получаемая устройством или совокупностью устройств.

Нагрузка потребителей – суммарная электрическая мощность потребителей системы (района, узла и т. д.).

Нагрузка электрическая расчетная – значение мощности (тока), по которой производится выбор параметров электрооборудования, выполняются расчеты режимов распределения мощности и напряжения в электрической сети.

Напряжение линейное – напряжение между фазными проводами электрической сети.

Напряжение номинальное – напряжение, на которое спроектирована сеть или оборудование и к которому относят их рабочие характеристики.

Напряжение фазное – напряжение между фазным проводом и нейтралью.

Нейтраль (нейтральная точка) – общая точка соединенных в звезду обмоток (элементов) электрооборудования.

Обмотка трансформатора – совокупность витков, образующих электрическую цепь, в которой суммируются электродвижущие силы, наведенные в витках, с целью получения высшего, среднего или низшего напряжения трансформатора или с другой целью.

Примечания. 1. В трехфазном и многофазном трансформаторе (трансформаторной группе) под «обмоткой» подразумевается совокупность соединяемых между собой обмоток одного напряжения всех фаз. 2. В однофазном трансформаторе под «обмоткой» подразумевается совокупность соединяемых между собой обмоток одного напряжения, расположенных на всех его стержнях.

Обмотка трансформатора вторичная – обмотка трансформатора, от которой отводится энергия преобразованного переменного тока.

Обмотка трансформатора первичная – обмотка трансформатора, к которой подводится энергия преобразуемого переменного тока.

Примечание. Термин применим к любому числу обмоток трансформатора, если направление передачи энергии от них к другим обмоткам трансформатора является определенным.

Объединенная энергосистема – совокупность нескольких энергетических систем, объединенных общим режимом работы.

Параметр электрической цепи (элемента электрической цепи) – величина, характеризующая какое-либо свойство электрической цепи (элемента электрической цепи) в качественном и количественном отношениях.

Проводимость (электрическая) комплексная – комплексная величина, равная отношению комплексного действующего значения синусоидального электрического тока в пассивной электрической цепи или в ее элементе к комплексному действующему значению синусоидального электрического напряжения на выводах этой цепи или на этом элементе.

Прогноз нагрузки – оценка ожидаемой нагрузки на определенный момент времени.

Расчет потокораспределения – расчет параметров электрической сети при установившемся режиме при заданных мощностях в узлах и напряжениях в некоторых из них.

12 3 4 5 6 Следующая ⇒