
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Свойства скалярного произведения ⇐ ПредыдущаяСтр 3 из 3
1. Скалярное произведение обладает переместительным свойством: ab=ba
5. Если векторы а и b(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а b .
Выражение скалярного произведения через координаты Пусть заданы два вектора
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:
т.е
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат. 2.Определение векторного произведения Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму векторуb виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).
Векторным произведением вектора а на вектор b называется вектор с, который: 1. Перпендикулярен векторам a и b, т. е. с а и с b; 2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и bкак на сторонах (см. рис. 17), т. е. 3.Векторы a, b и с образуют правую тройку.
Векторное произведение обозначается а х b или [а, b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i, j и k (см. рис. 18): i х j = k, j х k = i, k х i = j. 1) k i, k j; 2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1; 3) векторы i, j и k образуют правую тройку (см. рис. 16). Свойства векторного произведения 1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19). Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а, b, а хb и a, b, bxaпротивоположной ориентации). Стало быть axb = -(bxa ). 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. (а хb ) = ( а ) х b = а х ( b ).
Пусть > 0. Вектор (ахb ) перпендикулярен векторам а и b. Вектор ( а)хb также перпендикулярен векторам а и b (векторы а, а лежат в одной плоскости). Значит, векторы (ахb ) и ( а)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
Поэтому (a хb )= ахb. Аналогично доказывается при < 0. 3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b < => ахb =0.
В частности, i *i =j *j =k *k =0. 4. Векторное произведение обладает распределительным свойством: (a+b) хс= ахс+b хс. Примем без доказательства. Выражение векторного произведения через координаты Мы будем использовать таблицу векторного произведения векторов i, j и k:
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус». Пусть заданы два вектора а=ахi +ayj +azk и b =bxi +byj +bzk. Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
Полученную формулу можно записать еще короче:
так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки.Равенство (7.2) легко запоминается. Дополнительный вопрос Правила интегрирования. 1)∫ d(f(x))=f(x)+C; 2)d∫ f(x)dx=f(x)dx; 3)∫ kf(x)dx=kf(x)dx, где k — постоянная величина; 4)∫ (f(x))±g(x))dx=∫ f(x)dx±∫ g(x)dx; 5)∫ udv=uv-∫ vdu (интегрирование по частям); 6)∫ f(x)dx=F(x)+C 7) ∫ f(x)dx=F(x)+C 7.таблица неопределенных интегралов · ∫ xndx=xn+1/(n+1)+C, n · ∫ dx/x=lnІxІ+C · ∫ axdx =ax/lna + C · ∫ exdx=ex+C · ∫ sinxdx=-cosx +C · ∫ cosxdx=sinx +C · ∫ dx/cos2x=tgx+C · ∫ dx/sin2x=-ctgx +C · ∫ dx/(1+x2)=arctgx+C · или ∫ dx/(1+x2) =-arcctgx+C · ∫ dx/ · или ∫ dx/ · ∫ dx/(a2+x2)= · ∫ dx/(a2+x2)=- · ∫ dx/ · ∫ dx/ ·∫ dx/ Таблица производных
8. ДОПОЛНИТЕЛЬНЫЙ Формула Ньютона-Лейбница Если
ЭТО ЕСЛИ ВСЕ РАСПИСАТЬ: Если функция f (x) интегрируема на [a; b], то для любого
который называется интегралом с переменным верхним пределом. Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке. Если функция f интегрируема на [a; b] и непрерывна в
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.
Одним из основных результатов математического анализа является теорема Ньютона – Лейбница: Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a). Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β ],
Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:
Эллипс(основной 11)
12)Гипербола
a2 b2
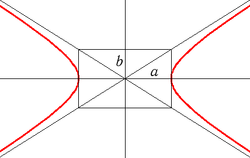 y2 x2 y2 x2
b2 a2
Линиями второго порядка называются линии, уравнения которых имеют вторую степень. Парабола Параболой называется множество всех точек равноудалённых от данной точки (фокуса) и от данной прямой (директрисы).
Окружность Окружность- множество всех точек равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
|
Последнее изменение этой страницы: 2017-03-14; Просмотров: 401; Нарушение авторского права страницы