
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Геометрический смысл дифференциалаСтр 1 из 5Следующая ⇒
Дифференциал функции Пусть функция
где
Замечание
Геометрический смысл дифференциала
Инвариантность формы записи
Инвариантность формы записи дифференциалов первого порядка Пример
Инвариантность формы записи дифференциалов второго порядка Однако, уже для второго порядка, это не верно: Упс! Инвариантности нет. Формула Лейбница . где
Эта формула доказывается по индукции аналогично биномиальным коэффициентам. 11.Вопрос.Основные теоремы о дифференциалах. Таблица дифференциалов. Основные теоремы дифференциального исчисления Теорема Ферма Теорема Теорема Ферма. (О равенстве нулю производной) Тогда производная в этой точке равна нулю, то есть Следствие. (Геометрический смысл теоремы Ферма) В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс. Теорема Ролля Теорема Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения) 1. Тогда на интервале Следствие. (Геометрический смысл теоремы Ролля) Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс. Следствие. Если Теорема Лагранжа
Теорема Коши
Таблица дифференциалов
12.Вопрос.Применение дифференциалов в приближённых вычислениях значений функций. Дифференциалы высших порядков.Примеры. Применение дифференциала в приближенных вычислениях формулы:
Дифференциалы высших порядков Дифференциал второго порядка обозначается следующим образом:
Аналогично определяются дифференциалы более высоких порядков. Определение Дифференциалом
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев. Случай независимой переменной Первый дифференциал функции
где
. То есть дифференциал второго порядка
Для вычисления дифференциала
Итак,
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
Пример Задание. Найти дифференциал третьего порядка функции Решение. По формуле
Случай зависимой переменной Пусть задана дифференцируемая функция
где
Пример Задание. Найти дифференциал второго порядка
Найдем все необходимые компоненты формулы. Из условия имеем: Из того, что
13 Вопрос. Правило Лопиталя, применение его к вычислению пределов. Примеры. Правило Лопиталя . Именно правила Лопиталя расправляются с пределами, в которых имеет место неопределённость Первое правило Лопиталя
И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость Вернёмся к Примеру 5 первой статьи о пределах, в котором был получен следующий результат: К неопределённости 0: 0 применим первое правило Лопиталя:
Применим правило Лопиталя: Второе правило Лопиталя
Примечание : предел Важно, чтобы была неопределённость Проверим Пример №3 первого урока: Пример 1 Вычислить предел Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя: Теорема (Правило Лопиталя). Пусть функции 1) эти функции дифференцируемы в окрестности точки 2) 3) 4) Тогда существует и Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций. Замечание Правило Лопиталя распространяется на случай неопределенности типа Пример Задание. Найти Решение. Получим неопределенность и для решения предела воспользуемся правилом Лопиталя.
Ответ. Замечание Правило Лопиталя распространяется и на случай Замечание Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми. Замечание правило Лопиталя работает только с неопределенностями Вопрос.Раскрытие неопределённостей различных видов.Примеры. Определение При вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределенностями. Основные виды неопределенностей: Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение. Основные пределы 1. Первый замечательный предел:
Пример Задание. Вычислить предел Решение. Получим неопределенность, сделаем замену. При
Ответ. Задание. Найти предел Решение. Ответ. 4. Предел целой рациональной функции: если
Вопрос.Условия монотонности дифференцируемой функции. Примеры. Определение Функция
Пример Функция для Определение Функция
Пример Функция для Функция Определение Функция Функция Теорема (Об условии возрастания/убывания монотонной функции) Если производная функции Замечание Если функция возрастает на промежутке, то Пример Задание. Исследовать функцию Решение. Найдем производную заданной функции:
Для любого действительного Ответ. Функция Вопрос. Экстремумы функций (необходимые и достаточные условия существования) экстремума. Примеры Понятие экстремума функции Определение точка локального максимума точка локального минимума Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
строгого локального минимума строгое неравенство Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом. Замечание Теорема (Необходимое условие экстремума) Если функция
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки - это либо стационарные точки (решения уравнения Замечание Не в каждой своей критической точке функция обязательно имеет максимум или минимум. Теорема (Первое достаточное условие экстремума) Пусть для функции 1. функция непрерывна в окрестности точки 2. 3. производная Тогда в точке Если производная Таким образом, для того чтобы исследовать функцию 1. найти производную 2. найти критические точки, то есть такие значения 3. исследовать знак производной слева и справа от каждой критической точки; 4. найти значение функции в экстремальных точках. Пример Задание. Исследовать функцию Решение. Находим производную заданной функции:
Далее ищем критические точки функции, для этого решаем уравнение
Первая производная определена во всех точках. Таким образом, имеем одну критическую точку
Так как при переходе через точку Замечание. Также можно определить интервалы монотонности функции: так как на интервале Ответ. Теорема (Второе достаточное условие экстремума) Пусть для функции 1. она непрерывна в окрестности точки 2. первая производная 3. Тогда в точке Вопрос. Наибольшее и наименьшее значение непрерывной на отрезке функции. Примеры. . Функция 1) она непрерывна на интервале Функция
Вторая теореме Вейерштрасса, непрерывная на отрезке Число В нашем случае: Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка. Важно! Как уже заострялось внимание в статье об экстремумах функции, наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ, что максимум функции и минимум функции. Так, в рассматриваемом примере число Кстати, а что происходит вне отрезка Пример 1 Найти наибольшее и наименьшее значения функции Вопрос.Выпуклость и вогнутость прямой. Примеры. Теорема (Об условиях выпуклости или вогнутости графика функции) Пусть функция Определение Точкой перегиба графика функции Теорема (О необходимом условии существования точки перегиба) Если функция Теорема (О достаточном условии существования точки перегиба) Если: 1. первая производная 2. вторая производная 3. тогда в точке Пример Задание. Найти интервалы выпуклости/вогнутости функции Решение. Найдем вторую производную заданной функции:
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение
Исследуем знак второй производной слева и справа от полученной точки:
Так как на промежутке Ответ. Точка На промежутке 19 Вопрос. Точки перегиба( необходимые и достаточные условия существования перегиба). Примеры.
Точки перегиба Пусть f′ ′ (x0)=0, f′ ′ ′ (x0)≠ 0. Тогда точка x0 является точкой перегиба функции f(x). в точке x0 либо строго возрастает (если f′ ′ ′ (x0)> 0), либо строго убывает (если f′ ′ ′ (x0)< 0). Так как f′ ′ (x0)=0, то вторая производная при некотором δ > 0 имеет разные знаки в левой и правой δ -окрестности точки x0. Отсюда, на основании предыдущей теоремы, следует что x0 − точка перегиба функции f(x). | ||||||||||||||||||
Вопрос. Понятие первообразной и неопределённого интеграла. Основные свойства неопределённого интеграла. Примеры.
Неопределенный интеграл. Понятие первообразной
Первообразная, основные понятия и определения
Определение
Функция 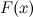 называется первообразной для функции
называется первообразной для функции 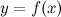 на промежутке
на промежутке 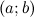 , конечном или бесконечном, если функция
, конечном или бесконечном, если функция 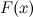 дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
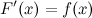
Последнее равенство можно записать через дифференциалы:
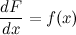 или
или 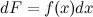
Функция 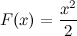 является первообразной для функции
является первообразной для функции 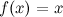 , так как
, так как
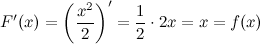
Первообразная 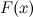 имеет конечную производную, а, следовательно, является непрерывной функцией.
имеет конечную производную, а, следовательно, является непрерывной функцией.
Теорема
(О бесконечном множестве первообразных для функции)
Если функция 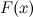 является первообразной для функции
является первообразной для функции 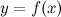 на некотором промежутке, то и функция
на некотором промежутке, то и функция 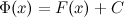 , где
, где 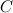 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции 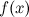 на рассматриваемом промежутке.
на рассматриваемом промежутке.
для функции 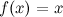 первообразной является функция
первообразной является функция 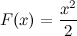 , а, следовательно, и все функции вида
, а, следовательно, и все функции вида 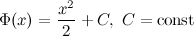 также будут первообразными, так как выполняется равенство
также будут первообразными, так как выполняется равенство 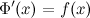 :
:
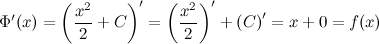
Таким образом, если функция 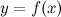 имеет первообразную, то она имеет бесконечное множество первообразных.
имеет первообразную, то она имеет бесконечное множество первообразных.
Теорема
(Об общем виде первообразной для функции)
Если функции 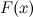 и
и 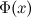 - две любые первообразные функции
- две любые первообразные функции 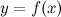 , то их разность равна некоторой постоянной, то есть
, то их разность равна некоторой постоянной, то есть
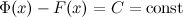
Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции 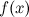 , может быть представлена в виде
, может быть представлена в виде 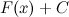 .
.
Неопределенный интеграл
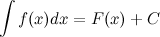
Знак 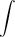 называется интегралом,
называется интегралом, 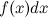 - подынтегральным выражением,
- подынтегральным выражением, 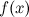 - подынтегральной функцией, а
- подынтегральной функцией, а  - переменной интегрирования.
- переменной интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции 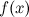 называется интегрированием функции
называется интегрированием функции 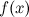 . Интегрирование представляет собой операцию, обратную дифференцированию.
. Интегрирование представляет собой операцию, обратную дифференцированию.
Теорема
Каждая непрерывная на промежутке 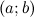 функция, имеет на этом интервале первообразную.
функция, имеет на этом интервале первообразную.
Свойства неопределенного интеграла
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению
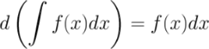
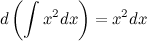
2. Производная от неопределенного интеграла равна подынтегральной функции
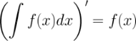
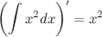
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
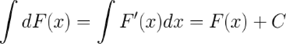
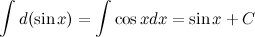
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
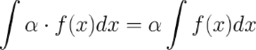
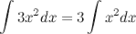
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций
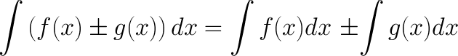
Последнее изменение этой страницы: 2017-03-15; Просмотров: 430; Нарушение авторского права страницы