
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Элементы теории погрешностейСтр 1 из 7Следующая ⇒
Ю. Я. Кацман
ПРИКЛАДНАЯ МАТЕМАТИКА Численные методы Учебное пособие
Томск 2000 УДК 519.6(075.8)
Кацман Ю. Я. Прикладная математика. Численные методы. Учебное пособие. – Томск: Изд. ТПУ, 2000. – 68 с.
В пособии в краткой форме изложены теоретические вопросы первой части курса прикладной математики, рассмотрены наиболее известные и широко применяемые методы вычислений. Каждая тема, при необходимости. иллюстрируется графически, после рассмотрения теоретического материала даны примеры расчетов. В конце каждого раздела приведены вопросы для самоконтроля. Пособие подготовлено на кафедре вычислительной техники, соответствует программе дисциплины и предназначено для студентов Центра дистанционного образования.
Печатается по постановлению Редакционно-издательского Совета Томского политехнического университета.
Рецензенты:
А.И. Кочегуров – доцент факультета систем управления Томского университета систем управления и радиоэлектроники.
В.И. Рейзлин – доцент кафедры автоматизации проектирования Томского политехнического университета.
Темплан 2000
© Томский политехнический университет, 2000 1. Элементы теории погрешностей..................................................................................... 5 2. Численное интегрирование.............................................................................................. 8 2.1. Постановка задачи................................................................................................................. 8 2.2. Формула прямоугольников................................................................................................... 9 2.3. Формула трапеций............................................................................................................... 10 2.4. Формула Симпсона.............................................................................................................. 11 2.5. Вычисление определенных интегралов методами Монте-Карло................................... 13 3. Численное решение систем линейных алгебраических уравнений (СЛАУ) 16 3.1. Решение задач линейной алгебры...................................................................................... 16 3.2. Метод Гаусса......................................................................................................................... 18 3.3. Схема Гаусса с выбором главного элемента..................................................................... 22 3.4. Вычисление обратной матрицы методом Гаусса............................................................. 24 3.5. Вычисление определителей методом Гаусса.................................................................... 25 3.6. Метод простой итерации (метод Якоби)........................................................................... 27 3.7. Метод Зейделя...................................................................................................................... 28 3.8. Метод скорейшего спуска (градиента) для случая системы линейных 4. Приближенное решение нелинейных и трансцендентных уравнений............ 35 4.1. Постановка задачи............................................................................................................... 35 4.2. Графическое решение уравнений....................................................................................... 35 4.3. Метод половинного деления (дихотомии)........................................................................ 36 4.4. Метод хорд............................................................................................................................ 37 4.5. Метод Ньютона (метод касательных)................................................................................ 38 4.6. Комбинированный метод.................................................................................................... 40 5. Приближенное решение систем нелинейных уравнений..................................... 42 5.1. Метод Ньютона.................................................................................................................... 42 5.2. Метод градиента (метод скорейшего спуска)................................................................... 45 6. Решение обыкновенных дифференциальных уравнений.................................... 48 6.1. Методы решения задачи Коши........................................................................................... 48 6.2. Метод рядов, не требующий вычисления производных правой части уравнения....... 50 6.3. Метод Рунге-Кутта............................................................................................................... 51 6.4. Многошаговые методы........................................................................................................ 53 6.5. Экстраполяционные методы Адамса................................................................................. 54 6.6. Интерполяционные методы Адамса.................................................................................. 55 7. Интерполирование и приближение функций........................................................... 57 7.1. Задача интерполирования и аппроксимации функций................................................... 57 7.2. Интерполирование алгебраическими многочленами...................................................... 58 7.3. Интерполяционная формула Ньютона.............................................................................. 59 7.4. Сходимость интерполяционного процесса....................................................................... 61 7.5. Задача обратного интерполирования................................................................................. 62 7.6. Отыскание параметров эмпирических формул методом наименьших квадратов........ 63 7.7. Суть метода наименьших квадратов.................................................................................. 63 Литература............................................................................................................................... 68 Вопросы для самопроверки
· Дайте определения и приведите примеры устранимой и неустранимой погрешностей. · Что такое погрешность округления? Какова ее связь с разрядностью ЭВМ? · Как вычислить относительную погрешность, зная абсолютную? · Как по абсолютной погрешности вычислить относительную погрешность?
Численное интегрирование Постановка задачи
Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой. Мы будем рассматривать способы приближенного вычисления определенных интегралов
основанные на замене интеграла конечной суммой:
где Сk- числовые коэффициенты, а xk Î [a, b], k = 0, 1, …, n. Приближенное равенство
называется квадратурной формулой, а x k – узлами квадратурной формулы. Погрешность квадратурной формулы определяется соотношением
В общем случае погрешность квадратурной формулы (2.4) зависит как от выбора коэффициентов Ск , так и от расположения узлов хк. Введем на отрезке [a, b] равномерную сетку с шагом h, тогда xi = a + ih, где (i = 0, 1, ..., n;
Таким образом, для построения формулы численного интегрирования на отрезке [a, b] достаточно построить квадратурную формулу на частичном отрезке [xi-1, xi] и воспользоваться формулой (2.5).
Формула прямоугольников
На частичном отрезке [xi-1, xi] заменим подынтегральную функцию полиномом Лагранжа нулевого порядка, построенным в одной точке. Естественно в качестве этой точки выбрать среднюю: xi-0.5 = xi - 0.5h. Тогда получим формулу
Подставив (2.6) в (2.5), получим составную формулу средних прямоугольников:
Графическая иллюстрация метода средних прямоугольников представлена на рис. 2.1.
Рис. 2.1. Интегрирование методом средних прямоугольников
Погрешность формулы (2.7) определяется выражением
Здесь Замечание. Формулу (2.7) можно представить в ином виде:
Эти формулы в выражении (2.9) называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис. 2.2.
а) б) Рис. 2.2. Метод левых (а) и правых (б) прямоугольников
Однако из-за нарушения симметрии в формулах (2.9) их погрешность значительно больше, чем в методе средних прямоугольников и ~ O(h).
Формула трапеций
Если на частичном отрезке подынтегральную функцию заменить полиномом Лагранжа первой степени, то есть
тогда искомый интеграл запишется следующим образом:
После подстановки выражения (2.11) в (2.5) составная формула трапеций примет вид
Графически метод трапеций представлен на рис. 2.3.
Рис. 2.3. Метод трапеций
Погрешность формулы (2.12) определяется выражением:
Таким образом, погрешность метода трапеций Ψ ~ O(h² ) , но она в два раза больше, чем для формулы средних прямоугольников.
Формула Симпсона
В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки
Проведя интегрирование, получим:
Это и есть формула Симпсона или формула парабол. На отрезке
Графическое представление метода Симпсона показано на рис. 2.4.
Рис. 2.4. Метод Симпсона
Избавимся в выражении (2.16) от дробных индексов, переобозначив переменные:
Тогда формула Симпсона примет вид
Погрешность формулы (2.18) оценивается следующим выражением:
где h·n = b - a,
Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на четное число интервалов.
2.5. Вычисление определенных интегралов методами
Рассматриваемые ранее методы называются детерминированными, то есть лишенными элемента случайности. Методы Монте–Карло (ММК) – это численные методы решения математических задач с помощью моделирования случайных величин. ММК позволяют успешно решать математические задачи, обусловленные вероятностными процессами. Более того, при решении задач, не связанных с какими-либо вероятностями, можно искусственно придумать вероятностную модель (и даже не одну), позволяющую решать эти задачи. Рассмотрим вычисление определенного интеграла
При вычислении этого интеграла по формуле прямоугольников интервал [a, b] разбиваем на N одинаковых интервалов, в серединах которых вычислялись значения подынтегральной функции. Вычисляя значения функции в случайных узлах, можно получить более точный результат:
Здесь γ i - случайное число, равномерно распределенное на интервале На рис. 2.5 представлена графическая реализация метода Монте-Карло вычисления однократного интеграла со случайными узлами (2.21) и (2.22).
Рис. 2.5. Интегрирование методом Монте-Карло (1-й случай)
Однако при вычислении кратных интегралов детерминированными методами оценка погрешности перерастает в задачу порой более сложную, чем вычисление интеграла. В то же время погрешность вычисления кратных интегралов ММК слабо зависит от кратности и легко вычисляется в каждом конкретном случае практически без дополнительных затрат. Рассмотрим еще один метод Монте-Карло на примере вычисления однократного интеграла:
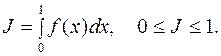 (2.23) (2.23)
Рис. 2.6. Интегрирование методом Монте-Карло (2-й случай) Как видно на рис. 2.6, интегральная кривая лежит в единичном квадрате, и если мы сумеем получать пары случайных чисел, равномерно распределенных на интервале [0, 1], то полученные значения (γ 1, γ 2) можно интерпретировать как координаты точки в единичном квадрате. Тогда, если этих пар чисел получено достаточно много, можно приблизительно считать, что
Пример 2.1. Вычислить следующий интеграл:
Поставленная задача была решена различными методами. Полученные результаты сведены в табл. 2.1. Таблица 2.1
Замечание. Выбор табличного интеграла позволил нам сравнить погрешность каждого метода и выяснить влияние числа разбиений на точность вычислений.
Вопросы для самопроверки
· Сформулируйте задачу численного интегрирования. · Метод средних, левых и правых прямоугольников. Что можно сказать об их погрешности, трудоемкости? · Задача численного интегрирования решена методом трапеций. Предложите и обоснуйте пути повышения точности (уменьшения погрешности) расчетов. · Сравните метод трапеций и метод Симпсона. · Какие методы Монте–Карло численного интегрирования вы знаете? Сравните эти методы с любым детерминированным. · Необходимо вычислить интеграл методами трапеций, Симпсона и ММК, разбив область интегрирования на 77 интервалов (точек). Что можно сказать о точности и применимости этих методов? 3. Численное решение систем линейных
Пример 3.1.
Для матрицы A порядка n > 4 непосредственное нахождение обратной матрицы A- 1 требует много времени (операций). Поэтому формула (3.5) на практике употребляется достаточно редко. Обычно значения неизвестных xi (i = 1, 2, ... n) могут быть получены по известным формулам Крамера:
Здесь матрица Ai получается из матрицы A заменой её i-го столбца столбцом свободных членов.
Пример 3.2. Решим вышеприведенную систему по формулам Крамера:
Применяемые в настоящее время методы решения СЛАУ можно разбить на две группы: точные и приближённые. Точными методами называются такие методы, которые в предположении, что вычисления ведутся точно (без округлений), за конечное число действий позволяют получить точные значения неизвестных xi. Приближенными методами называются такие методы, которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение системы (x1, x2, ..., xn) лишь с заданной точностью. Точное решение СЛАУ в этих случаях может быть получено теоретически как результат бесконечного процесса. К приближенным методам относятся метод простой итерации, метод Зейделя и т.п.
Метод Гаусса
Наиболее распространенным методом решения СЛАУ является метод Гаусса, в основе которого лежит идея последовательного исключения неизвестных. Существуют различные схемы, реализующие данный метод. Рассмотрим одну из них – схему единственного деления. Для простоты ограничимся рассмотрением СЛАУ с четырьмя неизвестными:
Пусть a11¹ 0 (ведущий элемент). Разделив первое уравнение на a11, получим первую главную строку:
где
Используя уравнение (3.8), можно исключить неизвестные x1 из 2-го, В результате получим систему из трех уравнений:
где коэффициенты
Далее первое уравнение системы (3.9) делим на ведущий элемент
где
Аналогично предыдущему шагу, исключая x2, как и x1, получим систему
Здесь Разделив первое уравнение системы (3.12) на
где
Теперь с помощью уравнения (3.13) исключим x3 из второго уравнения системы (3.12), окончательно получим:
где
Таким образом, исходную систему (3.7) привели к составленной из главных строк (3.8), (3.11), (3.13) и (3.14) эквивалентной системе с треугольной матрицей(3.15):
Из (3.15) последовательно находим
Итак, решение СЛАУ (3.7) распадается на два этапа: · прямой ход (приведение системы (3.7) к треугольному виду (3.15)); · обратный ход (определение неизвестных по формуле (3.16)).
Пример 3.3.
Прямой ход:
Из выражений (3.10) вычислим коэффициенты
Аналогично вычислим коэффициенты
Разделив первое уравнение системы на
Значит, Из (3.12) вычислим
Аналогично, вычислив коэффициенты для i = 4, получим:
Разделив первое уравнение на a(2)33 = 16.425, получим:
где По формуле (3.14) находим коэффициенты
и записываем одно уравнение с одним неизвестным:
1.1199786x4 = -1.1199768.
x1 + 0.5x2 - 0.05x3 + 0.5x4 = 1.35; x2 + 13.4x3 - 29x4 = 71.2; x3 - 1.72298x4 = 4.72298; 1.11998x4 = -1.11998. На этом закончен прямой ход. Обратный ход:
x4 = -1.000; x3 = 4.72298 - 1.72298 = 3; x2 = 71.2 - 13.4 * 3-29 = 2; x1 = 1.35 - 0.5 * 2 + 0.05 * 3 + 0.5 = 1.
Пример 3.5.
Замечания · При наличии решения, точные методы всегда дадут его через конечное число шагов. · В рамках точных методов вычислительная погрешность увеличивается с ростом размеров СЛАУ и не может быть уменьшена. Метод Зейделя
Этот метод представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной x i учитываются уже вычисленные ранее (k+1)-е приближения (x1 x2, ..., xi-1). Пусть дана приведенная линейная система:
Выберем произвольно начальные приближения корней Предположим, что k-е приближение
(k = 0, 1, 2,...).
Обычно процесс Зейделя сходится быстрее, чем метод Якоби. Бывает, что процесс Зейделя сходится, когда простая итерация расходится и, т.п. Правда, бывает и наоборот. Во всяком случае, достаточные условия сходимости для метода Якоби достаточны и для сходимости метода Зейделя. Если выполняется достаточное условие сходимости для системы (3.35) – по строкам, то в методе Зейделя выгодно расположить уравнения (3.36) так, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов:
Пример 3.6.
Для того чтобы обеспечить достаточные условия сходимости итерационного процесса (преобладающие значения диагональных элементов), преобразуем исходную систему и приведем к удобному виду. Чтобы дальнейшие преобразования были понятны, обозначим уравнения исходной системы буквами А, Б, В и Г соответственно:
х1= -0.2х2 +0.1х3 – 0.2х4 – 0.4; (Г) х2 = -0.2х1 – 0.2х3 + 0.2; (А – Б) х3 = 0.2х1 – 0.4х2 + 0.2х4 – 0.4; (Б) х4 = 0.333х1 - 1.111. (2А – Б + 2В – Г)
Преобразованную систему будем решать методом Зейделя, тогда, с учетом требования (3.37), окончательно получим:
В качестве нулевого приближения (k = 0) возьмем
Таблица 3.1
В приведенной таблице кроме значений неизвестных на каждом шаге оценивались невязки. Вспомним, что корнями уравнения Анализ данных, приведенных в табл. 3.1, показывает, что итерационный процесс быстро сходится, о чем свидетельствуют как быстрое уменьшение невязок, так и уменьшение изменений неизвестных (см. формулу (3.31) метода Якоби).
3.8. Метод скорейшего спуска (градиента) для случая
В рассматриваемом ниже итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге (максимально приблизиться к корню). Представим систему линейных уравнений в следующем виде:
Запишем выражение (3.38) в операторной форме:
Здесь приняты следующие обозначения:
В методе скорейшего спуска решение ищут в виде
где
а
В формуле (3.43) используется скалярное произведение двух векторов, которое определяется следующей формулой:
В формуле (3.43)
Нетрудно убедиться, что для системы (3.39) матрица Якоби равна
Как и для метода простой итерации, достаточным условием сходимости метода градиента является преобладание диагональных элементов. В качестве нулевого приближения можно взять
Замечания · Как видно из выражения (3.45), матрица Якоби не зависит от шага итерации. · Требования минимизации погрешности на каждом шаге обусловили то, что метод градиента более сложен (трудоемок), чем методы Якоби и Зейделя. · В методе градиента итерационный процесс естественно закончить при достижении
Обсуждение · В приближенных методах можно обеспечить практически любую погрешность, если итерационный процесс сходится. · Итерационный процесс можно прервать на любом k–ом шаге и продолжить позднее, введя в качестве нулевого шага значения x(k). · В качестве недостатка приближенных методов можно отметить то, что они часто расходятся, достаточные условия сходимости (преобладание диагональных элементов) можно обеспечить только для небольших систем из 3 – 6 уравнений.
Пример 3.7. Методом скорейшего спуска решим систему уравнений
Так как диагональные элементы матрицы являются преобладающими, то в качестве начального приближения выберем:
Следовательно, вектор невязок на нулевом шаге равен
Далее последовательно вычисляем
Отсюда причем
Аналогично находятся последующие приближения и оцениваются невязки. Что касается данного примера, можно отметить, что итерационный процесс сходится достаточно медленно (невязки уменьшаются).
Вопросы для самопроверки
· Назовите известные вам методы решения СЛАУ. · Чем точные методы отличаются от приближенных? · Что такое прямой и обратный ход в методе Гаусса? · Нужен ли обратный ход при вычислении методом Гаусса а) обратной матрицы; б) определителя? · Что такое невязка? · Сравните достоинства и недостатки точных и приближенных методов. · Что такое матрица Якоби? · Надо ли пересчитывать матрицу Якоби на каждом шаге итерации в методе градиента? · Исходная СЛАУ решается независимо тремя методами – методом Якоби, методом Зейделя и методом градиента. Будут ли равны значения а) начального приближения (нулевой итерации); б) первой итерации? · При решении СЛАУ (n > 100) итерационными методами решение расходится. Как найти начальное приближение? 4. Приближенное решение нелинейных Постановка задачи
Пусть дано уравнение
f(x) = 0 , (4.1)
где функция f(x) определена и непрерывна в конечном или бесконечном интервале a < x < b. Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ ) = 0, называется корнем уравнения (4.1) или нулем функции f(x). Предположим, что уравнение (4.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения. Приближенное нахождение изолированных действительных корней уравнения (4.1) складывается обычно из двух этапов: 1. Отделение корней, то есть установление возможно тесных промежутков [α, β ], в которых содержится один и только один корень исходного уравнения (4.1). 2. Уточнение приближенных корней, то есть доведение их до заданной степени точности.
Метод хорд
Пусть дано уравнение
f(x) = 0 , (4.4)
где функция f(x)определена и непрерывна на интервале [a, b] и выполняется соотношение f(a)·f(b) < 0. Пусть для определенностиf(a) < 0, f(b) > 0. Тогда вместо того, чтобы делить отрезок [a, b] пополам, более естественно разделить его в отношении
x1 = a + h1, (4.5) где
Далее этот прием применяем к одному из отрезков[a, x1] или [x1, b], на концах которого функция f(x) имеет противоположные знаки. Аналогично находим второе приближение x2 и т.д. (см. рис. 4.2.). Геометрически этот способ эквивалентен замене кривойy = f(x) хордой, проходящей через точкиА(a, f(a)) и B(b, f(b)).
Рис. 4.2. Уточнение корня уравнения методом хорд Действительно, уравнение хорды АВ имеет вид
Учитывая, что при х = х1 => y = 0, получим
Полагая, что на отрезке [a, b] вторая производная f'' ( x ) сохраняет постоянный знак, метод хорд сводится к двум различным вариантам: 1. Из рис. 4.2, a видно, что неподвижна точка а, а точкаb приближается к ξ, то есть
Преобразовав выражение (4.9), окончательно получим
2. Из рис. 4.2, bвидно, что точкаb остается неподвижной, а точкаа приближается к ξ, тогда вычислительная формула примет вид
Таким образом, для вычисления корня уравнения имеем две различные вычислительные формулы (4.10) и (4.11). Какую точку брать за неподвижную? Рекомендуется в качестве неподвижной выбирать ту точку, в которой выполняется соотношение
f(x)·f”(x) > 0. (4.12) Комбинированный метод
Пусть f(a)·f(b) < 0, а f¢ (x) и f¢ ¢ (x) сохраняют постоянные знаки на отрезке [a¸ b]. Соединяя метод хорд и метод касательных, получаем метод, на каждом шаге которого находим значения по недостатку и значения по избытку точного корня ξ уравненияf(x) = 0. Теоретически здесь возможны четыре случая:
· f¢ (x) > 0; f¢ ¢ (x) > 0; |
Последнее изменение этой страницы: 2017-03-15; Просмотров: 436; Нарушение авторского права страницы