
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Множества, операции над множествами.Стр 1 из 4Следующая ⇒
Введение Дискретная математика – область математики, занимающаяся изучением свойств структур конечного характера, которые возникают как внутри математики, так и в её приложениях. К числу таких конечных структур могут быть отнесены, например, конечные группы, конечные графы, а также некоторые математические модели преобразователей информации, конечные автоматы, машина Тьюринга и т. п. Дискретная (конечная) математика – это раздел математики, не связанный с понятиями предела, непрерывности и бесконечности. Дискретная математика имеет широкий спектр приложений, прежде всего в областях, связанных с информационными технологиями и компьютерами (компьютер – цифровая вычислительная машина, следовательно, имеет дискретный характер работы). В отличие от Д. м., классическая математика в основном занимается изучением свойств объектов непрерывного характера. Использование классической математики или Д. м. как аппаратов исследования связано с тем, какие задачи ставит перед собой исследователь и, в связи с этим, какую модель изучаемого явления он рассматривает, дискретную или непрерывную. Само деление математики на классическую и дискретную в значительной мере условно, поскольку, например, с одной стороны, происходит активная циркуляция идей и методов между ними, а с другой – часто возникает необходимость исследования моделей, обладающих как дискретными, так и непрерывными свойствами одновременно. Следует отметить также, что в математике существуют подразделы, использующие средства дискретной математики для изучения непрерывных моделей, и, наоборот, часто средства и постановки задач классического анализа используются при исследовании дискретных структур. Д. м. представляет собой важное направление в математике, в котором можно выделить характерные для Д. м. предмет исследования, методы и задачи, специфика которых обусловлена в первую очередь необходимостью отказа в Д. м. от основополагающих понятий классической математики - предела и непрерывности - и в связи с этим тем, что для многих задач Д. м. сильные средства классической математики оказываются, как правило, мало приемлемыми. Наряду с выделением Д. м. путём указания её предмета можно также определить Д. м. посредством перечисления подразделов, составляющих Д. м. К ним в первую очередь должны быть отнесены комбинаторный анализ, графов теория, теория кодирования, теория функциональных систем и некоторые другие. Элементы Д. м. возникли в глубокой древности и, развиваясь параллельно с другими разделами математики, в значительной мере являлись их составной частью. Типичными для того периода были задачи, связанные со свойствами целых чисел и приведшие затем к созданию теории чисел. К их числу могут быть отнесены отыскания алгоритмов сложения и умножения натуральных чисел у древних египтян (2-е тыс. до н. э.), задачи о суммировании и вопросы делимости натуральных чисел в пифагорийской школе (6 в. до н. э.) и т. п. Позже (17-18 вв.), в основном в связи с игровыми задачами, появились элементы комбинаторного анализа и дискретной теории вероятностей (Б. Паскаль, П. Ферма и др.), а в связи с общими проблемами теории чисел, алгебры и геометрии (18-19 вв.) возникли важнейшие понятия алгебры, такие как группа, поле, кольцо и др. (Ж. Лагранж, Э. Галуа и др.), определившие развитие и содержание алгебры на много лет вперёд и имевшие по существу дискретную природу. Стремление к строгости математических рассуждений и анализ рабочего инструмента математики – логики привели к выделению ещё одного важного раздела математики – математической логики (19-20 вв.). Однако наибольшего развития Д. м. достигла в связи с запросами практики, приведшими к появлению новой науки – кибернетики и её теоретической части – математической кибернетики (20 в.). Дискретная математика, по существу, стала активно развиваться с начала XX века, когда стали изучаться возможности формализации математики и были получены фундаментальные результаты в области математической логики. Информатизация и компьютеризация общества во второй половине XX века в значительной степени стимулировала развитие дискретной математики. Математическая кибернетика, непосредственно изучающая с позиций математики самые разнообразные проблемы, которые ставит перед кибернетикой практическая деятельность человека, является мощным поставщиком идей и задач для Д. м., вызывая к жизни целые новые направления в Д. м. Так, прикладные вопросы, требующие большой числовой обработки, стимулировали появление сильных численных методов решения задач, оформившихся затем в вычислительную математику, а анализ понятий " вычислимость" и " алгоритм" привёл к созданию важного раздела математической логики - теории алгоритмов. Растущий поток информации и связанные с ним задачи хранения, обработки и передачи информации привели к возникновению теории кодирования; экономические задачи, задачи электротехники, равно как и внутренние задачи математики, потребовали разработки теории графов; задачи конструирования и описания работы сложных управляющих систем составили теорию функциональных систем и т. д. В то же время математическая кибернетика широко использует результаты Д. м. при решении своих задач. Основные разделы дискретной математики: 1. Теория множеств. 2. Алгебраические структуры. 3. Логика и булевы функции. 4. Комбинаторика. 5. Теория графов. 6. Теория кодирования. 7. Логические исчисления и др.
Множества. Сравнение множеств. Множество А содержится во множестве В (множество В включает множество А, множество А является подмножеством В), если каждый элемент множества А является элементом множества В. Обозначение: А А Два множества называются равными, если они являются подмножествами друг друга. Обозначение: А=В. А=В Если непустое множество А является подмножеством В и множества А и В не являются равными, то А является собственным подмножеством В. Пример: М={4, 6, 8, 10}, К={6, 8}; К Для множеств существует понятие мощность. Для конечных множеств мощность совпадает с количеством элементов. Пример: | Операции над множествами.
Объединение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А или множеству В. Обозначение: А А Пересечение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и множеству В. Обозначение: А А Разность двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и не принадлежащие множеству В. Обозначение: А \ В. А \ В={x| х Обычно элементы множеств выбираются из некоторого достаточно широкого множества U, которое называется универсум. В связи с этим понятием можно ввести операцию дополнение. Дополнением множества А называется множества, которое состоит из элементов универсума, не принадлежащих множеству А. Обозначение:
Пример: U={1, 2, 3, 4, 5, 6, 7}, A={1, 2, 3, 4, 5}, В={2, 4, 6}. А В \ А = {6} Для наглядного изображения соотношений между множествами и изображения результатов операций над множествами используют диаграммы Эйлера.
B Отношения. Упорядоченные пары. Если a и b – объекты, то через (a, b) обозначим упорядоченную пару. Равенство упорядоченных пар определяется следующим образом: (a, b) = (c, d) Т. е. (a, b) Пример: (3, 4) Комбинаторика Введение При решении многих практических задач приходится выбирать из некоторой совокупности объектов элементы, обладающие тем или иным свойством, подсчитать число различных комбинаций и т.п. Такие задачи называются комбинаторными, а раздел математики, занимающийся такого рода задачами, называется комбинаторикой. Рассмотрим элементарный жизненный пример. Пусть некоторое агентство недвижимости располагает базой данных из n записей, каждая запись содержит одно предложение (что имеется) и один запрос (что требуется). Требуется найти все такие пары записей, в которых предложение первой записи совпадает с запросом второй (осуществить подбор вариантов обмена). Допустим, что используемая СУБД позволяет проверить вариант за одну миллисекунду. При «лобовом» алгоритме поиска вариантов (каждая запись сравнивается с каждой) потребуется n(n-1)/2 сравнений. Если n=100, то ответ будет получен через 4, 95 секунд; но если n=100000, то ответ будет получен за 4 999 950 секунд, что составляет почти 1389 часов и вряд ли это может считаться приемлемым. При этом мы оценили только трудоемкость прямых вариантов, но есть варианты, когда число участников сделки больше двух … Этот пример показывает, что комбинаторные вычисления помогают осуществить предварительный анализ и количественную оценку исходных задач и используемых алгоритмов. Основным инструментом такого анализа являются законы и формулы комбинаторики. Правило суммы. Задача: на блюде лежат 5 яблок и 2 груши. Сколькими способами можно выбрать один плод? Решение: плод можно выбрать семью способами (5+2=7). Если некоторый элемент a может быть выбран из множества элементов m способами, а другой элемент b может быть выбран n способами, причем любой выбор элемента b отличен от любого выбора элемента a, то выбрать либо a, либо b можно m + n способами. На языке теории множеств это правило формулируется следующим образом: Теорема1: если пересечение конечных множеств пусто, то число элементов в их объединении равно сумме чисел элементов множеств А и В. А Разберем случай, когда множества могут иметь непустые пересечения. Теорема2: для любых конечных множеств верно равенство: | А Задача: среди студентов первого курса 30 человек имеют дома компьютер, 35 – учебник по информатике; оказалось, что 10 студентов имеют и компьютер, и учебник по информатике. Сколько студентов на первом курсе? Решение: пусть множество А составляют студенты, имеющие компьютер, множество В – студенты, имеющие учебник по информатике; по условию задачи: |A| = 30 |B| = 35 | А | А Правило произведения. Вторым основным правилом комбинаторики является правило произведения. Задача: определить количество клеток в игре «морской бой», если номер клетки состоит из буквы (букв 10) и цифры (цифр тоже 10). Решение: количество клеток равно 10•10=100. Если элемент a можно выбрать из множества элементов m способами и после каждого такого выбора элемент b можно выбрать n способами, то два элемента (упорядоченную пару) a и b можно выбрать m•n способами. На языке множеств это правило выражается в виде следующей теоремы. Теорема3: если множества А и В конечны, то |A Следствие: если множества А1, А2, …, Аn - конечны, то |A1 Задача: сколько номеров, состоящих из двух букв, за которыми идут три цифры можно составить, если использовать 29 букв и 10 цифр. Решение: обозначим множество букв А, множество цифр – В; каждый номер требуемого вида является набором длины n из декартова произведения А | А
Формулы комбинаторики Перестановки Перестановки с повторениями Рассматривая различные перестановки, мы предполагали, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., nk элементов к-го вида, то имеем перестановки с повторениями, их число:
Задача: сколько различных «слов» можно составить из букв слова ДЕД, МАТЕМАТИКА. Решение: имеем перестановки с повторениями. А) ДЕД n=3, k=2, n1=2, n2=1 P3(2, 1) = 3! /(2! • 1! ) = 6 / 2 = 3; Б) МАТЕМАТИКА n=10, k=6, n1=2, n2=3, n3=2, n4=n5=n6=1 P10(2, 3, 2, 1, 1, 1)=10! /(2! • 3! • 2! )=2•4•5•6•7•9•10 = 134 400. Размещения Размещения без повторений. Размещениями называют комбинации, составленные из n данных элементов по k элементов (k< =n, k> 0), которые отличаются либо составом элементов, либо порядком расположения элементов. Обозначаются размещения Ank. А - первая буква французского слова arrangement, что в переводе означает " размещение", " приведение в порядок". Число всех возможных размещений находится по формуле: Задача: расписание одного дня состоит из двух пар. Определить число вариантов расписания при выборе из пяти дисциплин, если не может быть одинаковых пар. Решение: имеем размещения без повторений из пяти элементов по два, из число: Размещения с повторениями. Пусть существуют n различных элементов. Выберем из них m штук, действуя по следующему принципу: возьмем любой элемент, но не будем устанавливать его в какой-либо ряд, а просто запишем под номером 1 его название, сам же элемент вернем к остальным элементам. Затем опять из всех n элементов выберем один, запишем его название под номером 2 и снова вернем элемент обратно. Будем выполнять эти операции, пока не получим m названий. Размещения с повторениями вычисляются по формуле:
Задача: сколько четырехзначных номеров можно составить из 10 цифр? Решение: имеем размещения с повторениями из 10 элементов по 4, их число: Сочетания Сочетания без повторений. Сочетаниями называют комбинации, составленные из n различных элементов по k (k =< n) элементов, которые отличаются хотя бы одним элементом. Сочетания обозначаются: Cnk C - первая буква французского слова combinasion - сочетание. Составим из n элементов всевозможные сочетания по k элементов в каждом. Их будет Cnk. Внутри каждого сочетания, состоящего из k элементов, образуем всевозможные комбинации, учитывающие порядок следования в них элементов. Таких комбинаций будет Pk, т.к. мы в нашем сочетании образовываем перестановки. Всего различных комбинаций из n элементов по k в каждой, отличающихся друг от друга либо составом (элементами), либо порядком их следования, будет Cnk • Pk. Но такие комбинации называются размещениями. Таким образом, Ank = Cnk • Pk, тогда:
Задача: в шахматном турнире участвует 7 человек; сколько партий будет сыграно, если между любыми двумя участниками должна быть сыграна партия? Решение: имеем сочетания без повторений из 7 элементов по 2; их число: Сочетания с повторениями. Если в сочетаниях некоторые элементы (или все) могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями. Их число определяется по формуле: Задача: сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных? Решение: имеем сочетания с повторениями из четырех по 7 по, их число: 3. Графы.. 2 3.1. Основные понятия. 2 3.1.1. История теории графов. 2 3.1.2. Определения. 3 3.1.3. Смежности и инцидентность. 4 3.1.4. Изоморфизм графов. 5 3.2. Представление графов в ЭВМ.. 6 3.2.1. Требования к представлению графов. 6 3.2.2. Матрица смежности. 7 3.2.3. Матрица инциденций. 7 3.3. Геометрическая реализация графов. 8 3.4. Маршруты, цепи, циклы.. 8 3.4.1. Определения. 8 3.4.2. Эйлеровы графы.. 9 3.4.3. Гамильтоновы графы.. 10 3.5. Заключение. 12
Графы Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании. Дело в том, что теория графов предоставляет очень удобный язык для описания программных (да и многих других) моделей. Этот тезис можно пояснить следующей аналогией. Понятие отношения также можно полностью выразить через понятие множества. Однако независимое определение понятия отношения удобнее - введение специальных терминов и обозначений упрощает изложение теории и делает ее более понятной. То же относится и к теории графов. Стройная система специальных терминов и обозначений теории графов позволяют просто и доступно описывать сложные и тонкие вещи. Особенно важно наличие наглядной графической интерпретации понятия графа. Само название «граф» подразумевает наличие графической интерпретации. Картинки позволяют сразу «усмотреть» суть дела на интуитивном уровне, дополняя и украшая утомительные рациональные текстовые доказательства и сложные формулы. Основные понятия История теории графов Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач. 1 . Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку (рис. 3.1). Эта задача была решена Эйлером в 1736 году.
Рис. 3.1. Иллюстрация к задаче о Кенигсбергских мостах 2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 3.2). Эта задача была решена Куратовским в 1930 году.
Рис. 3.2. Иллюстрация к задаче о трех домах и трех колодцах Предметом первых задач теории графов были различные конфигурации, состоящие из точек и соединяющих их линий. При этом несущественно: являются ли эти линии прямыми или кривыми, длинными или короткими, тонкими или толстыми; важно только то, какие точки они соединяют. Т.о. граф – это абстрактное математическое понятие. Определения Графом G(V, E) называется совокупность двух множеств - непустого множества V ( множества вершин ) и множества Е неупорядоченных пар различных элементов множества V ( Е - множество ребер ). G(V, E): Число вершин графа G обозначим р, а число ребер – q. р(G) = |V| q(G) = |E|. Часто рассматриваются следующие родственные графам объекты. 1. Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным (или орграфом ). В этом случае элементы множества V называются узлами, а элементы множества 2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом). 3. Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом. Далее выражение: граф G(V, E) означает неориентированный граф без петель и кратных ребер. Обычно граф изображают диаграммой: вершины - точками (или кружками), ребра - линиями. Примеры. 1.
Т.о. это неориентированный граф с петлей и кратными ребрами. Рис. 3.3. Неориентированный граф с петлей и кратными ребрами. 2. Т.о. это ориентированный граф с петлей и кратными ребрами.
Рис. 3.4. Ориентированный граф с петлей и кратными ребрами.
3. 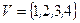 . .  , т.о. , т.о. 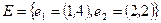
Рис. 3.5. Неориентированный граф с петлей.
Смежность и инцидентность Пусть v1, v2 - вершины, е = (v1, v2) - соединяющее их ребро. Тогда вершина v1 и ребро е инцидентны, вершина v2 и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. Степенью вершины v графа G(V, E) называется число ребер, инцидентных данной вершине. Обозначение: Вершина, имеющая степень 0 называется изолированной, имеющая степень 1 – висячей. Пример. Для графа, изображенного на рис. 3.5: вершина 3 – изолированная, вершины 1 и 4 - висячие. Пример. Для графа, изображенного на рис. 3.3. Ребро e1 инцидентно вершинам v1 и v2. Вершина v1 инцидентна ребрам e1 и e2. Ребра e1 и e2 – смежны. Вершины v1 и v2 – смежны.
Т.о. можно заметить, что Теорема Эйлера: Доказательство данной теоремы вытекает из того, что каждое ребро дает двойной вклад в сумму степеней вершин. Изоморфизм графов Говорят, что два графа G1(V1, E1) и G2(V2, E2) изоморфны (обозначается G1~ G2), если существует биекция h: V1 Графы рассматриваются с точностью до изоморфизма. Пример Три внешне различные диаграммы, приведенные на рис. 3.6, являются диаграммами одного и того же графа К3, 3.
Рис. 3.6. Диаграммы изоморфных графов Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, p(G) и q(G) - инварианты графа G. Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.
Рис. 3.8. Диаграммы неизоморфных графов с совпадающими инвариантами Представление графов в ЭВМ Следует подчеркнуть, что конструирование структур данных для представления в программе объектов математической модели - это основа искусства практического программирования. Мы приводим два различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Но все они, так или иначе, основаны на тех базовых идеях, которые описаны в этом разделе. Требования к представлению графов Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены два из наиболее часто используемых представления. Указанные представления пригодны для графов и орграфов, а после некоторой модификации также и для псевдографов, мультиграфов. Представления иллюстрируются на конкретных примерах графа G и орграфа D, диаграммы которых представлены на рис. 7.10.
Рис. 3.9. Диаграммы графа (слева) и орграфа (справа), используемых в качестве примеров Матрица смежности Представление графа с помощью квадратной булевской матрицы
отражающей смежность вершин, называется матрицей смежности, где
Пример
Матрица инциденций Представление графа с помощью матрицы Н: array [l..p, l..q] of 0..1 (для орграфов Н: array [l..p, l..q] of -1..1), отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа:
а для ориентированного графа
Пример
Маршруты, цепи, циклы Определения Маршрутом в графе G(V, E) называется чередующаяся последовательность вершин и ребер v1, e1, v2, e2, ..., vk, ek, vk+1, в которой любые два соседних элемента инцидентны. Это определение подходит также для псевдо-, мульти- и орграфов. Для «обычного» графа достаточно указать только последовательность вершин или только последовательность ребер. Если v1=vk+1, то маршрут замкнут, иначе открыт. Если все ребра различны, то маршрут называется цепью. Если все вершины цепи различны, то цепь называется простой. Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z(G) (является инвариантом). Граф без циклов называется ациклическим. Для орграфов цепь называется путем, а цикл - контуром. Пример В графе, диаграмма которого приведена на рис. 3.10: 1. v1, v3, v1, v4 - маршрут, но не цепь; 2. v1, v3, v5, v2, v3, v4 - цепь, но не простая цепь; 3. v1, v4, v3, v2, v5 - простая цепь; 4. v1, v3, v5, v2, v3, v4, v1- цикл, но не простой цикл; 5. v1, v3, v4 - простой цикл.
Рис. 3.10. Маршруты, цепи, циклы Две вершины графа называются связанными, если существует маршрут, соединяющий эти вершины. Граф называется связным, если любая пара его вершин связанна. Граф называется деревом, если он связен и не содержит циклов. Эйлеровы графы Вернемся к историческому примеру о Кенигсбергских мостах. В каком случае в графе можно найти цикл, в котором каждое ребро участвует ровно один раз? Цикл, содержащий каждое ребро ровно один раз, называется эйлеровым. Граф, содержащий эйлеровый цикл, называется эйлеровым графом. Теорема ( критерий эйлеровости графа ): конечный граф G(V, E) является эйлеровым, тогда и только тогда, когда он связен и степени всех его вершин – четны. Цепь, содержащая каждое ребро ровно один раз, называется эйлеровой. Граф, содержащий эйлерову цепь, называется полуэйлеровым графом. Теорема ( критерий полуйлеровости графа ): конечный граф G(V, E) является полуэйлеровым, тогда и только тогда, когда он связен и точно две го вершины имеют нечетную степень. Гамильтоновы графы Кроме эйлеровых графов рассматриваются также гамильтоновы графы. Название «гамильтонов цикл» произошло от задачи «Кругосветное путешествие», придуманной Гамильтоном в позапрошлом веке: нужно обойти все вершины графа, диаграмма которого показана на рис. 3.11 (в исходной формулировке это были названия столиц различных стран), по одному разу и вернуться в исходную точку. Этот граф представляет собой укладку додекаэдра.
Рис. 3.11. Задача «Кругосветное путешествие» Если граф имеет простой цикл, содержащий все вершины графа (по одному разу), то такой цикл называется гамильтоновым циклом, а граф называется гамильтоновым графом. Гамильтонов цикл не обязательно содержит все ребра графа. Ясно, что гамильтоновым может быть только связный граф. Теорема ( Дирак ). Если в графе G(V, E) для любой вершины v выполняется: Рассмотрим следующую задачу, известную как задача коммивояжера. Имеется р городов, расстояния между которыми известны. Коммивояжер должен посетить все р городов по одному разу, вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным. Очевидно, что задача коммивояжера - это задача отыскания кратчайшего гамильтонова цикла в полном графе. Можно предложить следующую простую схему решения задачи коммивояжера: сгенерировать все р! возможных перестановок вершин полного графа, подсчитать для каждой перестановки длину маршрута и выбрать из них кратчайший. Очевидно, такое вычисление потребует огромного количества шагов. Как известно, р! с ростом р растет быстрее, чем любой полином от р, и даже быстрее, чем 2Р. Таким образом, решение задачи коммивояжера описанным методом полного перебора оказывается практически неосуществимым даже для сравнительно небольших р. Более того, известно, что задача коммивояжера принадлежит к числу так называемых NP-полных задач. Вкратце суть проблемы NP-полноты сводится следующему. В различных областях дискретной математики, комбинаторики, логики и т. п. известно множество задач, принадлежащих к числу наиболее фундаментальных, для которых, несмотря на все усилия, не удалось найти алгоритмов решения, имеющих полиномиальную трудоемкость. Более того, если бы удалось отыскать эффективный алгоритм решения хотя бы одной из этих задач, то из этого немедленно следовало бы существование эффективных алгоритмов для всех остальных задач данного класса. На этом основано общепринятое мнение, что таких алгоритмов не существует. Полезно сопоставить задачи отыскания эйлеровых и гамилыоновых циклов, рассмотренные в этом и предыдущем разделах. Внешне формулировки этих задач очень похожи, однако они оказываются принципиально различными с точки зрения практического применения. Уже давно Эйлером получено просто проверяемое необходимое и достаточное условие существования в графе эйлерова цикла. Что касается гамильтоновых графов, то для них не известно необходимых и достаточных условий. На основе необходимого и досточного условия существования эйлерова цикла можно построить эффективные алгоритмы отыскания такого цикла. В то же время задача проверки существования гамильтонова цикла оказывается NP-полной (также как и задача коммивояжера). Известно, что почти нет эйлеровых графов, и эффективный алгоритм отыскания эйлеровых циклов редко оказывается применимым на практике. Теорема: Эйлеровых графов почти нет (E(p) – число эйлеровых графов с p вершинами, G(p) – число всех графов с p вершинами):
С другой стороны, можно показать, что почти все графы гамильтоновы. Теорема: (H(p) – число гамильтоновых графов с p вершинами, G(p) – число всех графов с p вершинами):
Таким образом, задача отыскания гамильтонова цикла или эквивалентная задача коммивояжера являются практически востребованными, но для них неизвестен (и, скорее всего, не существует) эффективный алгоритм решения. Заключение |
Последнее изменение этой страницы: 2017-03-15; Просмотров: 730; Нарушение авторского права страницы