Алгоритм двойственного симплексного метода
Для того чтобы решить задачу линейного программирования двойственным симплексным методом, необходимо выполнить следующее:
1. Привести задачу к каноническому виду.
2. Найти ПДОР с базисом из единичных векторов, вычислить оценки векторов-условий по базису этого решения и, если они согласуются с признаком оптимальности, то решать задачу двойственным симплексным методом.
3. Если ПДОР не имеет отрицательных координат, то оно является допустимым и оптимальным (по теореме 5.3). Решение задачи заканчивается.
4. Если ПДОР имеет отрицательную координату  < 0, для которой соответствующие коэффициенты разложений всех векторов условий неотрицательные (
< 0, для которой соответствующие коэффициенты разложений всех векторов условий неотрицательные (  ), то задача не имеет решения ввиду несовместности системы ограничений. Решение задачи прекращается.
), то задача не имеет решения ввиду несовместности системы ограничений. Решение задачи прекращается.
5. Если хотя бы одна координата ПДОР отрицательна, т. е.
 < 0 и при этом найдется хотя бы один отрицательный коэффициент
< 0 и при этом найдется хотя бы один отрицательный коэффициент  разложений векторов условий
разложений векторов условий  по базису решения, то переходят к новому решению, на котором значение целевой функции будет ближе к оптимальному. Номер вектора
по базису решения, то переходят к новому решению, на котором значение целевой функции будет ближе к оптимальному. Номер вектора  , вводимого в базис, находится с использованием параметра
, вводимого в базис, находится с использованием параметра
 .
.
Номер вектора  , выводимого из базиса, находится из условия
, выводимого из базиса, находится из условия  в задаче на максимум или
в задаче на максимум или  в задаче на минимум.
в задаче на минимум.
Далее переходят к пункту 3 данного алгоритма.
Пример 5.7. Решить двойственным симплексным методом


Решение. Приводим задачу к каноническому виду, для чего вводим в левые части ограничений-неравенств неотрицательные дополнительные переменные  :
:

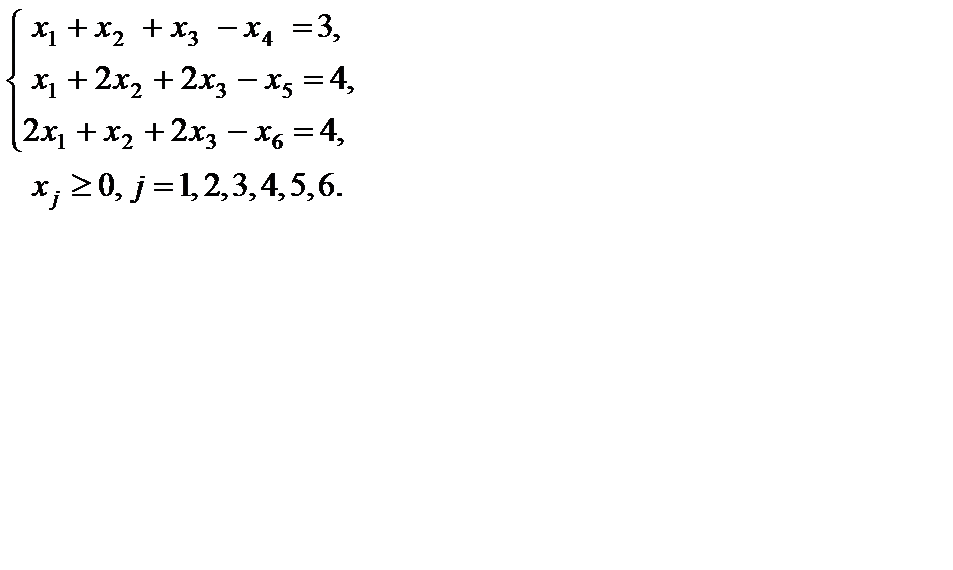
Для нахождения ПДОР с единичным базисом умножим каждое из ограничений на -1

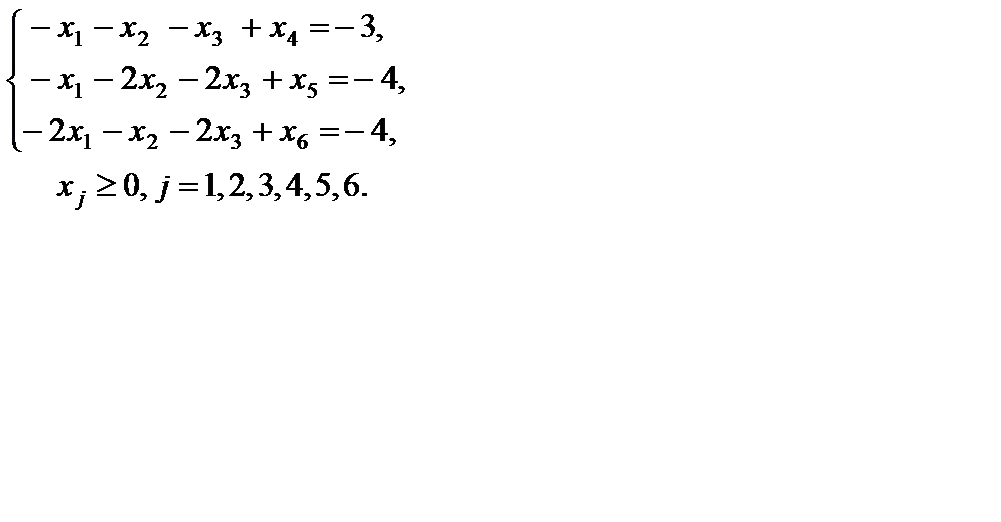
Находим начальное ПДОР  с базисом
с базисом  .
.
Вычисляем оценки  разложений векторов условий по базису ПДОР и заполняем первую симплексную таблицу (табл. 5.5).
разложений векторов условий по базису ПДОР и заполняем первую симплексную таблицу (табл. 5.5).
Т а б л и ц а 5.5

Оценки для векторов условий, не входящих в базис, положительные. Следовательно, условия применимости двойственного симплексного метода к задаче на отыскание максимума выполнены. Начальное ПДОР  не будет оптимальным, так как не удовлетворяет условиям неотрицательности переменных задачи. Переходим к новому ПДОР с неотрицательными оценками для векторов-условий. Для того чтобы оценки остались неотрицательными, необходимо номер k вектора
не будет оптимальным, так как не удовлетворяет условиям неотрицательности переменных задачи. Переходим к новому ПДОР с неотрицательными оценками для векторов-условий. Для того чтобы оценки остались неотрицательными, необходимо номер k вектора  , вводимого в базис, выбирать из условия
, вводимого в базис, выбирать из условия
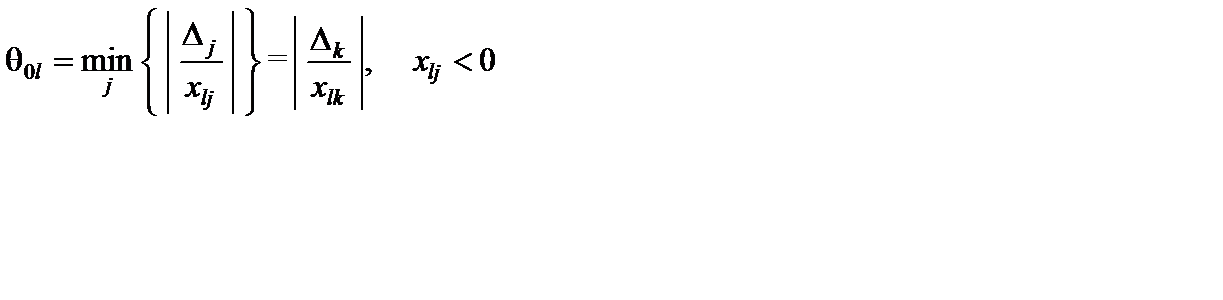 .
.
При этом номер l вектора  , выводимого из базиса, должен соответствовать отрицательной координате
, выводимого из базиса, должен соответствовать отрицательной координате  ПДОР. В данном случае отрицательными являются три координаты х4 = –3, х5 = –4, х6 = –4,. Для соответствующих строк (1-й, 2-й, 3-й) симплексной таблицы находим
ПДОР. В данном случае отрицательными являются три координаты х4 = –3, х5 = –4, х6 = –4,. Для соответствующих строк (1-й, 2-й, 3-й) симплексной таблицы находим
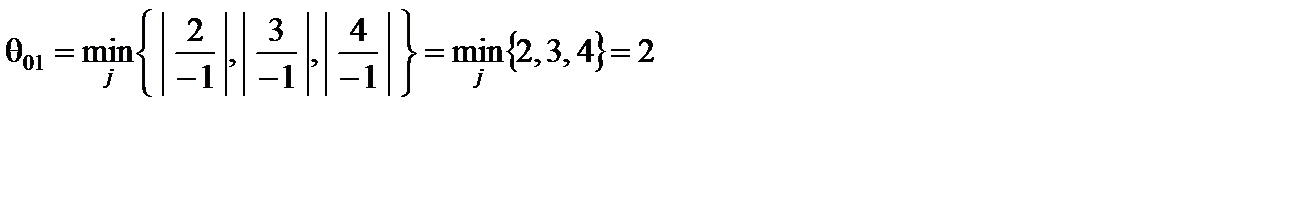 при j = 1;
при j = 1;
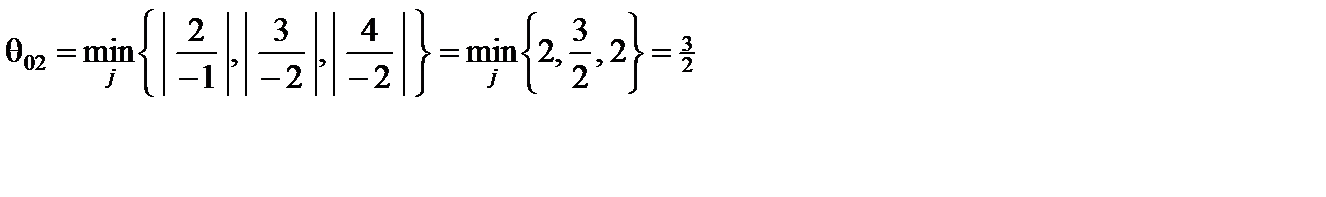 при j = 2;
при j = 2;
 при j = 1.
при j = 1.
Отсюда следует, что оценки для, не входящих в базис векторов-условий, останутся положительными, если при выведении первого вектора базиса  ввести в базис вектор
ввести в базис вектор  или при выведении второго вектора базиса
или при выведении второго вектора базиса  ввести вектор
ввести вектор  , или при выведении третьего вектора базиса
, или при выведении третьего вектора базиса  ввести вектор
ввести вектор  . Для обеспечения наибольшего приближения к экстремуму целевой функции задачи на отыскание максимума номер l вектора, выводимого из базиса, определим из условия (5.29)
. Для обеспечения наибольшего приближения к экстремуму целевой функции задачи на отыскание максимума номер l вектора, выводимого из базиса, определим из условия (5.29)
 ,
,
где  - приращение целевой функции при введение в базис ПДОР вектора
- приращение целевой функции при введение в базис ПДОР вектора  .
.
Вычисляем 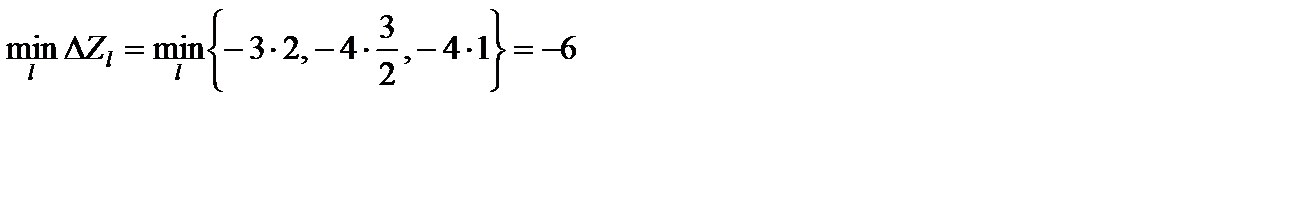 при l = 1, 2.
при l = 1, 2.
Номер вектора  определяется неоднозначно. По своему усмотрению выбираем l = 1, так как с разрешающим элементом
определяется неоднозначно. По своему усмотрению выбираем l = 1, так как с разрешающим элементом  легче производить дальнейшие вычисления, чем с разрешающим элементом
легче производить дальнейшие вычисления, чем с разрешающим элементом  .
.
Приходим ко второму ПДОР (табл.5.6).
Т а б л и ц а 5.6

Второе ПДОР  не будет оптимальным, так как не удовлетворяет условию неотрицательности. Для второй строки симплексной таблицы (табл. 5.6), в которой расположена отрицательная координата решения
не будет оптимальным, так как не удовлетворяет условию неотрицательности. Для второй строки симплексной таблицы (табл. 5.6), в которой расположена отрицательная координата решения 
 , находим
, находим
 при j = 2.
при j = 2.
Таким образом, из базиса ПДОР выводим вектор  , а вводим вектор
, а вводим вектор  , соответствующий минимуму отношения
, соответствующий минимуму отношения  . Приходим к третьему ПДОР (табл. 5.7).
. Приходим к третьему ПДОР (табл. 5.7).
Т а б л и ц а 5.7

Полученное решение  является оптимальным, так как удовлетворяет признаку оптимальности, т. е. не имеет отрицательных координат.
является оптимальным, так как удовлетворяет признаку оптимальности, т. е. не имеет отрицательных координат.
Ответ: max Z(X) = -7 при  .
.
Пример 5.8. Решить двойственным симплексным методом

Решение. Приводим задачу к каноническому виду
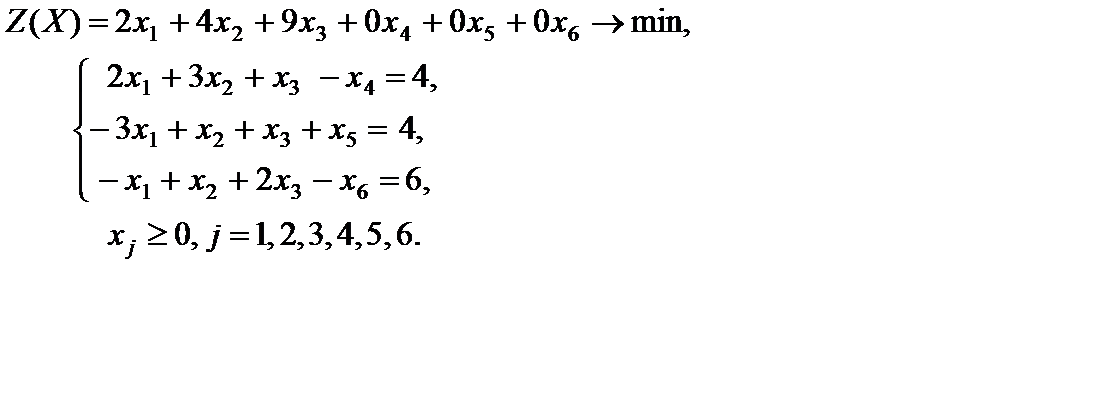
Для нахождения ПДОР с единичным базисом умножим первое и третье ограничение на -1,

Задача имеет начальное ПДОР  с базисом
с базисом  из единичных векторов. Оценки
из единичных векторов. Оценки  разложений векторов-условий
разложений векторов-условий  , не входящих в базис
, не входящих в базис  , отрицательны (табл. 5.8). Следовательно, данную задачу на отыскание минимума можно решить двойственным симплексным методом. Решение задачи приведено в табл. 5.8.
, отрицательны (табл. 5.8). Следовательно, данную задачу на отыскание минимума можно решить двойственным симплексным методом. Решение задачи приведено в табл. 5.8.
Т а б л и ц а 5.8

Начальное ПДОР  не является оптимальным, так как не удовлетворяет условиям неотрицательности. Переходим к следующему ПДОР. Необходимо один из векторов
не является оптимальным, так как не удовлетворяет условиям неотрицательности. Переходим к следующему ПДОР. Необходимо один из векторов  или
или  , которые соответствуют отрицательным координатам
, которые соответствуют отрицательным координатам  ,
,  решения
решения  , заменить одним из векторов
, заменить одним из векторов  или
или  . Номер k вектора
. Номер k вектора  , вводимого в базис, выбираем, используя условие (5.27). Находим
, вводимого в базис, выбираем, используя условие (5.27). Находим
 при j = 1.
при j = 1.
 при j = 2.
при j = 2.
Номер k вектора  , вводимого в базис, выбираем, используя условие (5.27). Находим
, вводимого в базис, выбираем, используя условие (5.27). Находим
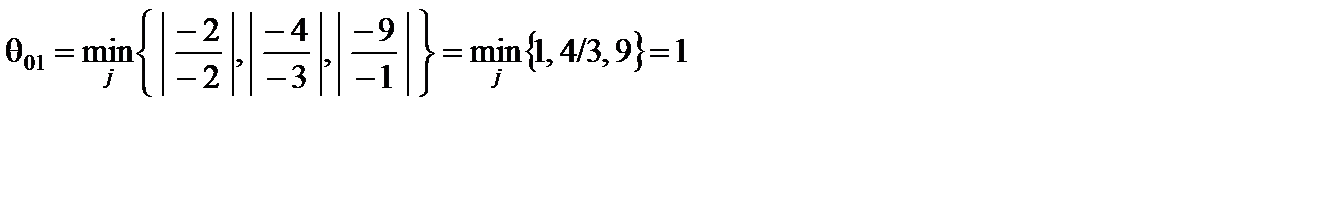 при j = 1.
при j = 1.
 при j = 2.
при j = 2.
Отсюда следует, что для того, чтобы оценки  при переходе к новому решению оставались неположительными, необходимо либо вектор
при переходе к новому решению оставались неположительными, необходимо либо вектор  заменить на
заменить на  , либо вектор
, либо вектор  на
на  . Для обеспечения наибольшего приближения к оптимальному решению в задаче на минимум номер l, выводимого из базиса вектора
. Для обеспечения наибольшего приближения к оптимальному решению в задаче на минимум номер l, выводимого из базиса вектора 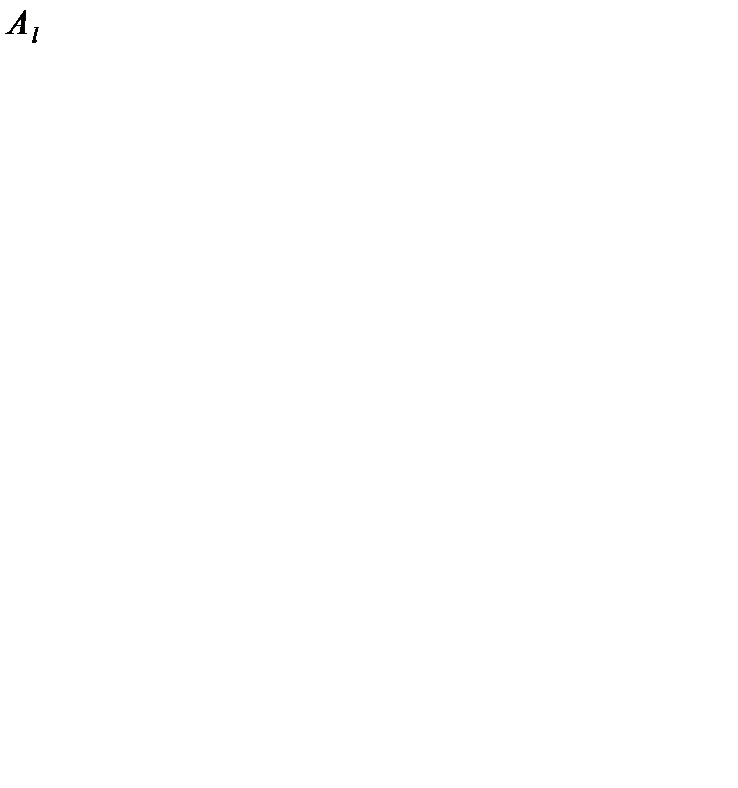 , определяется из условия (5.30)
, определяется из условия (5.30)
 .
.
Вычисляем
 при l = 3.
при l = 3.
Третий (l = 3) вектор базиса  заменяем вектором
заменяем вектором
 (
(  при j = 2). Выполняем преобразование Жордана с разрешающим элементом
при j = 2). Выполняем преобразование Жордана с разрешающим элементом  , получаем ПДОР
, получаем ПДОР  , которое не является оптимальным. Для второй строки второй симплексной таблицы, содержащей отрицательную координату
, которое не является оптимальным. Для второй строки второй симплексной таблицы, содержащей отрицательную координату  решения
решения  , находим
, находим
 при j = 3.
при j = 3.
Выводим из базиса  решения
решения  вектор
вектор  , вводим вектор
, вводим вектор  , переходим к ПДОР
, переходим к ПДОР  , которое является оптимальным, так как удовлетворяет условиям неотрицательности.
, которое является оптимальным, так как удовлетворяет условиям неотрицательности.
Ответ: min Z(X) = 26 при  .
.
Лекция №10
ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
Под названием " транспортная задача" объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены известным симплексным методом. Однако, ввиду того, что матрица системы ограничений транспортной задачи весьма своеобразна, для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить последовательность опорных решений, которая завершается оптимальным решением.


