Степенные ряды. Интервал сходимости.

Степенным рядом называется функциональный ряд вида (1) где , , , ..., , ... - постоянные числа, называемые коэффициентами ряда. Областью сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку. Для того, чтобы убедиться в этом, докажем сначала следующую теорему, очень важную для всей теории степенных рядов.

Теорема Абеля: 1) Если степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно сходится при всяком значении х, для которого ; 2) если ряд расходится при некотором значении , то он расходится при всяком х, для которого 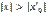. Док-во: 1) Так как, по предположению, числовой ряд 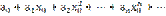(2)сходится, то его общий член при , а это значит, что существует такое положительное число М, что все члены ряда по абсолютной величине меньше М. Перепишем ряд в виде (3)и рассмотрим ряд из абсолютных величин его членов: (4)Члены этого ряда меньше соответствующих членов ряда (5) При последний ряд представляет геометрическую прогрессию со знаменателем и, следовательно, сходится. Так как члены ряда (4) меньше соответствующих членов ряда (5), то ряд (4) тоже сходится, а это и значит, что ряд (3) или (1) сходится абсолютно.

2) Теперь нетрудно доказать и вторую часть теоремы: пусть в некоторой точке 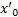ряд (1) расходится. Тогда он будет расходиться в любой точке x, удовлетворяющей условию . Действительно, если бы в какой-либо точке x, удовлетворяющей этому условию, ряд сходился, то, в силу только что доказанной первой части теоремы, он должен был бы сходиться и в точке , так как | |< |x|. Но это противоречит условию, что в точке х'0 ряд расходится. Следовательно, ряд расходится и в точке x. Таким образом, теорема полностью доказана.

Теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Действительно, если есть точка сходимости, то весь интервал заполнен точками абсолютной сходимости. Если х'0 — точка расходимости, то вся бесконечная полупрямая вправо от точки и вся полупрямая влево от точки - состоят из точек расходимости. Из этого можно заключить, что существует такое число R, что при мы имеем точки абсолютной сходимости, и при - точки расходимости. Таким образом, имеет место следующая теорема о строении области сходимости степенного ряда:

Теорема Областью сходимости степенного ряда является интервал с центром в начале координат. Интервалом сходимости степенного ряда называется такой интервал от -R до R что для всякой точки x, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек лежащих вне его, ряд расходится (рис.5). Число R называют радиусом сходимости степенного ряда. На концах интервала (т. е. при x= R и при x= - R) вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.

Отметим, что у некоторых рядов интервал сходимости вырождается в точку (R=0), у других охватывает всю ось Ox (R = ∞ ).

Укажем способ определения радиуса сходимости степенного ряда.

Пусть имеем ряд (1) Рассмотрим ряд, составленный из абсолютных величин его членов: (6) Для определения сходимости последнего ряда (с положительными членами! ) применим признак Даламбера. Допустим, что существует предел: Тогда по признаку Даламбера ряд (6) сходится, если т. е. если и расходится, если , т.е. если . Следовательно, ряд (1) сходится абсолютно при 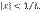.Если же , то и ряд (6) расходится, причем его общий член не стремится к нулю. Но тогда и общий член данного степенного ряда (1) не стремится к нулю, а это значит, на основании необходимого признака сходимости, что этот степенной ряд расходится (при ). Из предыдущего следует, что интервал есть интервал сходимости степенного ряда (1), т. е. Аналогичным образом для определения интервала сходимости можно пользоваться признаком Коши, и тогда .

 

 

25. Разложение функций в ряд Тейлора.

При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция определена в некоторой окрестности точки и имеет в этой точке производные всех порядков. Ряд

называется рядом Тейлора для функции в точке . При такой ряд называют также рядом Маклорена: . Функция может быть разложена в степенной ряд на интервале , если существует степенной ряд, сходящийся к на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки , то это ряд Тейлора. Пусть функция бесконечно дифференцируема на интервале и все ее производные ограничены в совокупности на этом интервале, то есть существует число , такое, что для всех и для всех справедливо неравенство 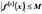. Тогда ряд Тейлора сходится к для всех . Приведем разложения в ряд Тейлора для основных элементарных функций.

,

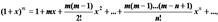
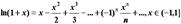
Разложение функций в степенные ряды.

Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции.

Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее. (См. Формула Тейлора).

Существует также способ разложения в степенной ряд при помощи алгебраического деления. Это – самый простой способ разложения, однако, пригоден он только для разложения в ряд алгебраических дробей.Пример. Разложить в ряд функцию .

Суть метода алгебраического деления состоит в применении общего правила деления многочленов.

 

Если применить к той же функции формулу Маклорена

,

то получаем:

……………………….

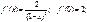
Итого, получаем:

Рассмотрим способ разложения функции в ряд при помощи интегрирования.

С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной.

Находим дифференциал функции и интегрируем его в пределах от 0 до х.

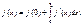
Пример. Разложить в ряд функцию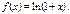

Разложение в ряд этой функции по формуле Маклорена было рассмотрено выше.

(См. Функция y = ln (1 + x)) Теперь решим эту задачу при помощи интегрирования.

При получаем по приведенной выше формуле:

Разложение в ряд функции может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.

 

Тогда получаем: Окончательно получим:

Пример. Разложить в степенной ряд функцию .

Применим разложение в ряд с помощью интегрирования.

Подынтегральная функция может быть разложена в ряд методом алгебраического деления:

 

Тогда Окончательно получаем:

⇐ Предыдущая1234

Поделиться: