Моделирование динамики адаптации при двух помехах

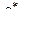k	S1(1) = j , S2(1)= −1 S1(2) = −1, S2(2)= 1		Sвых(1)(Tk)	Sвых(2)(Tk)	= −j, = −1  = −1, = 1		∆W1(Tk)	∆W2(Tk)
	W1(Tk)	W2(Tk)			R1(Tk)	R2(Tk)
0	0	0	1	1	− 1− j	0	0,1+ 0,1j	0
1	0,1+0,1j	0	0,9+0,1j	0,9−0,1j	−0,8−0,8j	−0,2j	0,07+0,07j	0,02j
2	0,17+0,17j	0,02j	0.83+0,15j	0.83−0,15j

Рис. 5.2. Трехэлементная ААР Аппелбаума

2. На рис. 5.2 представлена трехэлементная ААР по схеме Аппелбаума. Геометрия АР и положение  источника помехи повторяет ситуацию с ААР по рис. 5.1, причем аналогия усиливается еще и тем обстоятельством, что начальный весовой вектор* W₀ = {1, 0, 0} соответствует изотропной исходной ДН  F₀(θ). Продолжите табл. 5.3 на 3÷4 шага. Попробуйте найти установившееся состояние**. Объясните, почему процессы адаптации сопоставляемых ААР различаются.

Таблица 5.3

Динамика адаптации при одной помехе

k	S1 = 1	S2 = j	S3= -1	Sвых(Tk) = W1+jW2-W3	= 1	= -j	= -1	∆W1(T)	∆W2(T)	∆W3(T)
	W1(Tk)	W2(Tk)	W3(Tk)		R1(Tk)	R2(Tk)	R2(Tk)
0	1	0	0	1	1	− j	− 1	−0,2	0,1j	0,1
1	0,8	0,1j	0,1	0,6	0,6	− 0,6 j	− 0,6	−0,14	0,05j	0,05

Аналитическое решение

В соответствии с выражениями (4.24) градиента G₁ функционала Ф₁(W) для ААР по схеме Аппелбаума и ААР с основным элементом процессы антиградиентного спуска 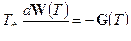 описываются следующими матричными дифференциальными уравнениями:

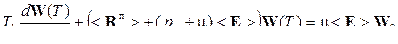,        (5.3΄)

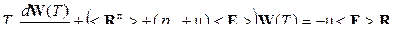,            (5.3˝)

которые являются компактной записью системы N дифференциальных уравнений. Каждое из уравнений (5.3) имеет одинаковую структуру:

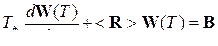,                           (5.4)

где < R > =  − эрмитово сопряженная матрица размерности NxN; В – N-мерный вектор (m W₀ или –m R₀ соответственно). Матричное уравнение (5.4) легко решается, если догадаться искать решение в виде разложения по собственным векторам матрицы < R > [20].

Собственным вектором A_i матрицы < A >  называется вектор, удовлетворяющий равенству:

< A > A_i = λ_i A_i.                       (5.5)

Число λ_i называется собственным числом матрицы < A >. У квадратной эрмитово сопряжённой матрицы < A >, т.е. матрицы, коэффициенты которой связаны равенством , все N ее собственных чисел вещественны и не отрицательны λ_i ≥ 0, а собственные векторы A_i взаимно ортогональны.

Особые ситуации возникают в случае кратных собственных чисел λ_i = λ_j (в том числе нулевых). Соответствующие этим числам собственные векторы определяются не однозначно, так как любая их линейная комбинация 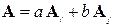 образует собственный вектор, соответствующий тому же собственному числу λ_i (или λ_j). Это неудобство легко преодолевается за счёт построения ортогональной последовательности (с помощью процедуры ортогонализации Шмидта см. раздел 2.3) из совокупности линейно независимых векторов, соответствующих кратному собственному числу.

Запишем искомый вектор W(T) и вектор В в виде разложений:

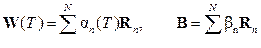,                    (5.6)

где R_n – собственные векторы матрицы < R > уравнения (5.4). Естественно, что временная зависимость вектора W проявляется во временной зависимости искомых коэффициентов α_n. Используя в уравнении (5.4) разложения (5.6) и учитывая свойство (5.5), получаем векторное равенство, т.е. равенство коэффициентов разложений левой и правой частей равенства:

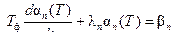;  (n = 1,...,N).         (5.7)

Таким образом, система дифференциальных уравнений (5.4) «распалась» на N не связанных друг с другом дифференциальных уравнений относительно коэффициентов разложений (5.6). Теоретически при T = ∞ весовой вектор достигает установившегося режима и перестает изменяться: 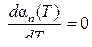, следовательно, имеем α_∞n = β_n/λ_n.

Уравнение (5.7) совпадает с уравнением ФНЧ (2.2). Его решение при ступенчатой функции β_n (в момент времени T = 0 возникает стабильная помеха) и произвольном состоянии ААР в начальный момент 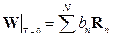 дается выражением (2.3), из которого следует:

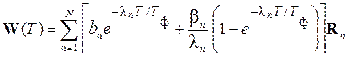,          (5.8)

где β_n – коэффициенты разложения вектора m W₀ или –m R₀ в зависимости от типа ААР.

Таким образом, расчет динамики процесса адаптации сводится к  проблеме поиска собственных векторов и чисел (спектра) матрицы* < R > = . С учетом свойств единичной матрицы для произвольного вектора R имеем (р_ш + m) < E > R = (р_ш + m) R, поэтому собственные векторы матриц < R > и 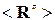 совпадают, и только значения их собственных чисел отличаются на (р_ш + m). В некоторых случаях спектр матрицы 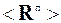, а вместе с ним и матрицы < R >, может быть найден аналитически, и тем самым определено решение (5.8).

Собственные векторы корреляционной матрицы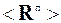

Матрицы 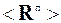и < Z >  – эрмитово сопряженные. Причём матрица < Z > взаимных сопротивлений в силу линейной независимости индивидуальных ДН {f_n(θ)} не является особенной и не имеет нулевых собственных чисел. Иначе обстоит дело с матрицей корреляции коэффициентов помеховых сигналов.

Ситуация с одиночной помехой

Если действует единственный источник помехи, и P₁, θ₁ – соответственно мощность мешающего сигнала и направление его прихода, то элементами матрицы служат коэффициенты . Таким образом, строка {R_n}, соответствующая индексу n, повторяет строку 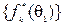 с точностью до постоянного сомножителя P₁ f_n(θ₁), и все строки матрицы  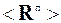оказываются линейно зависимыми.

Если обозначить через R₁ вектор-столбец, образованный компонентами 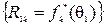, то легко убедиться в том, что R₁ является  собственным вектором матрицы 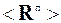, которому соответствует собственное число 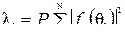. Действительно,

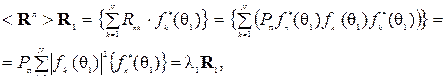    (5.9)

где 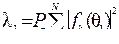. В частности, в случае изотропных элементов λ₁ = N P_П. Применительно к матрице < R > соответствующее собственное число определяется равенствами  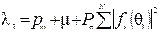или λ₁ = р_ш + m + N P_П.

Для любого вектора R ^┴ , ортогонального вектору R₁, т.е. для вектора, компоненты {R_n^┴} которого удовлетворяют равенству , имеем:

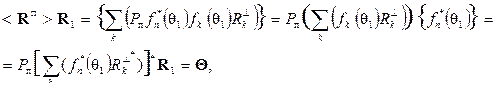  (5.10)

где через  обозначен нулевой вектор. Таким образом, в ситуации с одиночным источником мешающего сигнала любой вектор 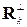 можно считать собственным вектором матриц  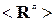и < R >, соответствующим нулевому собственному числу. Применительно к матрице < R > эти собственные числа имеют одинаковые значения λ_k^┴ = р_ш + m.

Воспользовавшись алгоритмом ортогонализации Шмидта (см. раздел  2.3),  из   произвольно    выбранных  N−1   линейно  независимых  N -мерных векторов R_k (k = 2,..., N) можно (и в упражнении 3 нужно будет) построить последовательность взаимно ортогональных векторов 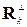, образующих вместе с вектором R₁ ортогональный базис N-мерного пространства весовых коэффициентов. Тогда любой вектор W представляется разложением:

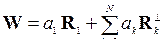,               (5.11)

в котором по понятным причинам выделено первое слагаемое. Как обычно (см. раздел 2.3 «Проектирование на подпространство»), коэффициенты разложения даются равенствами:

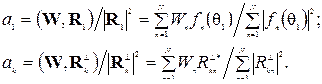          (5.12)

W → 1 1 0 В↓   P1 j P1 – P1         (1–j) P1

Рис. 5.3. Матрица <R> и умножение ее на вектор W

Упражнение 1. В выделенные жирными границами ячейки запишите* матрицу  для ААР и помеховой ситуации по рис. 5.2. Конечно же, мощность помехи P₁ можно принять за единицу, но целесообразно учесть ее как скалярный сомножитель перед матрицей  или как коэффициент у каждого элемента матрицы. Это позволит при последующих выкладках и вычислениях в явном виде прослеживать влияние мощности помехи на динамику процесса адаптации. Первая строчка этой матрицы заполнена для вашей уверенности. Освойте технику умножения матрицы на вектор-столбец: запишите вектор B = 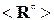W в правый столбец, выделенный серым цветом, используя в качестве вектора W вектор (1, 1, 0)^Т. Здесь знак ^Т символизирует транспонирование (преобразование строки (1, 1, 0) в столбец). По правилам матричной алгебры компоненты вектора B есть результат умножения соответствующей строки матрицы на вектор-столбец W. В нашем случае 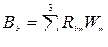. «Технологически» удобно вектор-столбец W записать строчкой над матрицей, как это показано на рис. 5.3. В интересах вашего самоконтроля приведено значение компоненты В₂.

Упражнение 2. Легко заметить, что вектор В предыдущего упражнения отличается от первого столбца матрицы 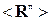, являющегося собственным вектором R₁, лишь коэффициентом*. Объясните этот факт двумя способами: 1) исходя из особенности структуры матрицы 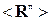, 2) раскладывая (мысленно) вектор W по собственным векторам матрицы  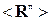и учитывая свойство собственных векторов и значения собственных чисел. Оба способа приводят к обобщению: отмеченное свойство матрицы  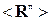имеет место при любом векторе W.

Упражнение 3. Постройте ортонормированную систему собственных векторов матрицы 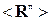 из упражнения 1. Собственный вектор R₁ совпадает с первым столбцом матрицы 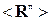, и поскольку он подлежит нормировке, то ради удобства его можно записать с точностью до произвольного скалярного коэффициента в форме R₁ = {1, −j, −1}. Нормировкой векторов займемся на последнем этапе. Следуя общей схеме, два недостающих собственных вектора можно построить из произвольно выбранных векторов. Заботясь о простоте вычислений, возьмем вектор r₂ = {1, 0, 0}. Используемый при ортогонализации коэффициент ξ₁ = (r₂, R₁) / ||R₁||² очевидно равен 1/3, потому после ортогонализации имеем 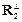= r₂ − ξ₁ R₁ = {2/3, j/3, 1/3}. Для удобства вычислений, не меняя обозначения, умножим этот вектор на 3, т.е. будем считать, что 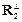= {2, j, 1}. Проверьте, действительно ли векторы R₁ и  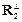ортогональны? При вычислении скалярного произведения не забудьте о комплексном сопряжении компонент второго вектора.

Теперь из вектора r₃ = {0, 0, 1} построим вектор 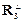= r₃ − ξ₁ R₁ − ξ₂ R₂, где ξ₁ = − 1/3, ξ₂ = 1/6, и после умножения на 2 получим 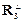= {0, −j, 1}. После нормировки, имеем , , . 

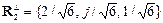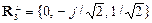Тренировка изобретательности. Ситуация, когда существует произвол в выборе чего-то, как правило, предоставляет возможности для творчества и изобретательности. Вспомните, хотя бы, как изящно Х.А. Лоренц распорядился неоднозначностью векторного потенциала А (знаменитая «калибровка Лоренца» в электродинамике). Естественно, масштаб нашей задачи не велик, но произволом в выборе векторов r₂ и r₃ можно изящно распорядиться. Действительно, что, кроме нежелания размышлять или не натренированной догадливости, мешает выбрать вектор r₂ = {1, 0, 1}, который ортогонален вектору R₁ и, следовательно, не требует никакой ортогонализации: 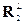 = {1, 0, 1}. Вдохновившись таким успехом, несложно прийти к идее выбрать вектор r₃ = {0, 1, 0}, который ортогонален вектору R₂ и, следовательно, потребуется его ортогонализация только к вектору R₁:

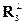 = r₃ − j R₁ /3 = {−j/3, 2/3, j/3} ~ {−j, 2, j}.

После нормировки получаем систему векторов:

, , ,

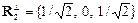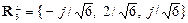эквивалентную предыдущей системе.

Ситуация с двумя помехами

Корреляционная матрица 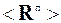 для ситуации, когда действуют М статистически независимых источников мешающих сигналов, есть сумма корреляционных матриц для каждого из источников (m = 1,..., М)

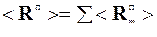.                   (5.13)

Поскольку каждая из матриц имеет единственное отличное от нуля собственное число λ_m и соответствующий ему собственный вектор R_m, то при M < N можно предложить следующий экономный в вычислительном отношении численный алгоритм определения спектра суммарной матрицы.

Начнем со случая двух источников помех, которым соответствуют корреляционные матрицы 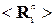 и 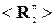. Обозначим через R₁ и R₂ нормированные собственные векторы этих матриц, т.е.

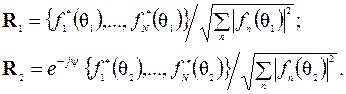    (5.14)

Для удобства дальнейших выкладок введен такой фазовый сомножитель 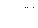, при котором скалярное произведение (R₁, R₂) = α  становится вещественной величиной.

Любой вектор R одновременно ортогональный и векторам R₁ и R₂ соответствует нулевому собственному числу обеих матриц 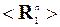 и 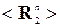, а потому и для суммарной матрицы это один из собственных векторов, соответствующих нулевому собственному числу. Таким образом, ненулевым собственным числам матрицы  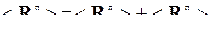соответствуют векторы, являющиеся линейными комбинациями векторов R₁ и R₂. Найдем эти векторы.

Запишем искомый собственный вектор в виде R_∑ = а₁ R₁ + а₂ R₂. В интересах умножения матриц 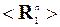 и  на «чужие» собственные векторы R₂ и R₁ соответственно, воспользуемся ортогональными разложениям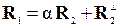и  и 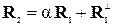, где с учётом нормированности векторов R₂, R₁ и фазового сомножителя  вещественный коэффициент α определяется скалярным произведением 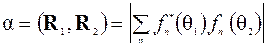. Тогда получаем:

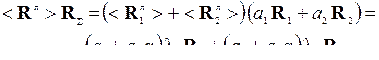
   (5.15)

Так как любой собственный вектор не перестает быть таковым после умножения на произвольный коэффициент, то, не теряя общности, одному из искомых коэффициентов можно задать произвольное ненулевое значение. Выберем , т.е. примем R_∑ = R₁ + а₂ R₂. Тогда получаем

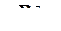R∑ = λ1 R1 + α λ2 R2 + α а2 λ1 R1 + а2 λ2 R2 =             =λ1 (1 + α a2) R1 + λ2 (α + а2) R2.

(5.16)

                  

 

Если R_∑ − собственный вектор матрицы 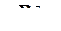, то правая часть равенства (5.16) с точностью до постоянного сомножителя повторяет этот вектор, т.е. выполняется пропорция a₂ λ₁ (1 + α a₂) = λ₂ (α + а₂), являющаяся квадратным уравнением относительно . Корни этого уравнения

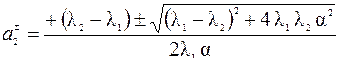        (5.17)

определяют два собственных вектора матрицы :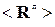

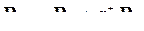 и .        (5.18)

Легко убедиться в том, что полученные векторы R_∑1 и R_∑2  ортогональны друг другу:

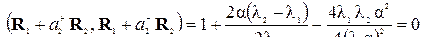,      (5.19)

как и должно быть для собственных векторов эрмитовой матрицы .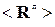

Собственные числа по определению (5.5) находятся по правилу, которое в компактной форме (с двухэтажными символами для компактности) записывается следующим образом:

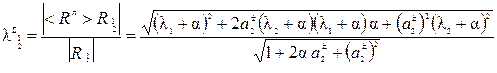.      (5.20)

В случае АР, состоящей из изотропных излучателей, собственные числа λ₁ и λ₂ корреляционных матриц 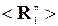 и 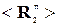 отдельных источников одинаковы и равны λ₁ = λ₂ = N P_П = λ. Тогда из (5.17) следует, что 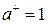, , 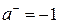а потому имеем

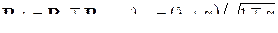.                        (5.21)

Аналогичные рассуждения применимы и в ситуации с M источниками помех. Однако проблема поиска коэффициентов a_i разложения 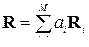 приводит к системе уравнений степени (M − 1), которую, естественно, приходится решать численно.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться: