Квадратурные формулы наивысшей алгебраической степени точности. Квадратурные формулы Гаусса

 

Если вопрос о точности вычисления интеграла стоит очень остро, то можно воспользоваться другими квадратурными формулами, в частности, квадратурными формулами наивысшей алгебраической степени точности, которая равна .

Пусть в квадратурном правиле

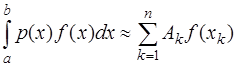           (7.4.27)

есть любой конечный или бесконечный отрезок и весовая функция  такова, что ее произведение на любую неотрицательную степень 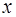 абсолютно интегрируемо на :

.

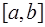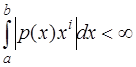Кроме того, будем считать функцию 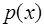 не эквивалентной нулю, то есть

.

Квадратурное правило (7.4.27) при фиксированном значении 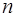 содержит  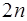параметров 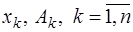, и выбрать их можно так, чтобы равенство (7.4.27) выполнялось точно для всех алгебраических многочленов степени не выше  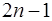или, что равносильно, чтобы выполнялись равенства:

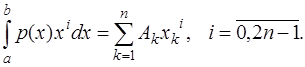            (7.4.28)

Равенства (7.4.28) образуют систему из 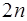 уравнений относительно  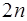неизвестных 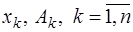, но в силу того, что данная система является нелинейной, ее решение весьма затруднительно.

Введем многочлен, корнями которого являются узлы квадратурного правила:

.             (7.4.29)

Для определения параметров квадратурного правила (7.4.27) доказаны следующие теоремы.

Теорема 1. Для того, чтобы квадратурное правило (7.4.27) было точным для всех алгебраических многочленов степени не выше 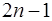, необходимо и достаточно, чтобы выполнялись следующие условия:

1) правило (7.4.27) было интерполяционным, то есть коэффициенты  определялись по формулам:

,              (7.4.30)

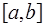2) многочлен  был ортогонален на  по весу  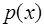ко всякому многочлену  степени меньшей :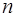

.                    (7.4.31)

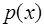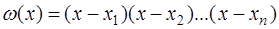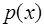Теорема 2. Если весовая функция  не меняет знак на , то существует и при этом единственный многочлен  ортогональный на  по весу  ко всякому многочлену  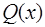степени меньшей .

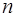Теорема 3. Если весовая функция 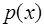 не меняет знак на  и многочлен  ортогонален на 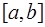 по весу  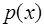ко всякому многочлену  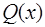степени, меньшей 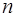, то все корни многочлена  действительные, различные и лежат внутри .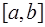

Теорема 4. Если весовая функция 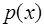 не меняет знак на , то ни при каком выборе  и  равенство (7.4.27) не может быть верным для всех многочленов степени .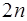

Приведенные теоремы доказывают справедливость следующего утверждения: если весовая функция  сохраняет знак на , то квадратурное правило (7.4.27), верное для всех многочленов степени не выше 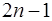, существует при всех  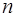и является единственным для каждого 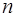. При этом для знакопостоянной весовой функции  степень точности  является наивысшей возможной. Таким образом, для конкретной весовой функции 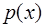 существует единственный многочлен , корни которого являются узлами квадратурного правила, а выражение (7.4.30) определяет коэффициенты этого правила.

Квадратурное правило наивысшей алгебраической степени точности для постоянной весовой функции  называется квадратурным правилом Гаусса. Отрезок интегрирования 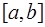 будем считать конечным. Всякий конечный отрезок  линейной заменой переменных

                        (7.4.32)

может быть преобразован в отрезок . Тогда выражение (7.4.27) может быть преобразовано к виду:

    (7.4.33)

Систему многочленов, ортогональную на , образуют многочлены Лежандра:

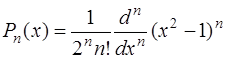.         (7.4.34)

Таким образом, в квадратурной формуле Гаусса узлы  должны располагаться в корнях многочлена Лежандра степени 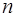 и в справочниках можно найти значения  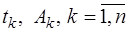для различных .

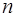Процесс вычисления интеграла методом Гаусса с точностью  можно организовать следующим образом. Задать конкретное значение 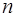 и выписать значения узлов  и коэффициентов  для этого 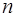. Затем строить последовательность значений интеграла , где величина 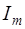 получается путем суммирования значений интегралов, вычисленных на  отрезках, полученных делением отрезк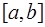а  на  частей. При этом каждый частичный отрезок переводится в 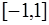 и интеграл для каждого частичного отрезка вычисляется при использовании одних и тех же значений . Интеграл будем считать вычисленным с заданной точностью , если для некоторого  выполнится неравенство:

.                        (7.4.35)

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться: