
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Раздел «Линейная алгебра»Стр 1 из 7Следующая ⇒
ВЫСШАЯ МАТЕМАТИКА. Раздел «Линейная алгебра» Электронное учебно-методическое пособие для студентов 1 курса экономического факультета Федеральное агентство по образованию ГОУ ВПО «Кемеровский государственный университет» Кафедра высшей математики ВЫСШАЯ МАТЕМАТИКА. Раздел «Линейная алгебра» Электронное учебно-методическое пособие для студентов 1 курса экономического факультета Кемерово 2009 Составитель: старший преподаватель Айнетдинова Л.Н. Высшая математика. Раздел «Линейная алгебра». Электронное учебно-методическое пособие для студентов 1 курса экономического факультета./ сост. Л.Н. Айнетдинова; ГОУ ВПО «Кемеровский государственный университет». – Кемерово, 2009. – 58 с. Электронное учебно-методическое пособие написано по курсу Высшая математика. Раздел «Линейная алгебра» для студентов 1 курса экономического факультета в соответствии с Государственным образовательным стандартом высшего профессионального образования. Учебно-методическое пособие содержит вопросы, которые необходимо знать для изучения предложенной темы практического занятия, разработаны примеры задач, приведены задачи для работы в аудитории и для самостоятельной работы.
Содержание СодержаниеВведение. 4 Введение. 5 Тема 1. 6 Матрицы.. 6 Примеры решения задач. 6 Тема 2. 10 Свойства определителей. 10 Примеры решения задач. 10 Тема 3. 14 Обратная матрица. Матричные уравнения. 14 Примеры решения задач. 14 Тема 4. 17 Система линейных алгебраических уравнений (СЛАУ) 17 Примеры решения задач. 17 Тема 5. 21 Ранг матрицы СЛАУ. 21 Примеры решения задач. 21 Тема 6. 25 Однородная система линейных уравнений. ФСР. 25 Примеры решения задач. 25 Тема 7. 28 Линейная зависимость векторов. 28 Базис и размерность линейного пространства. 28 Примеры решения задач. 29 Тема 8. 35 Линейные операторы. 35 Тема 9. 37 Квадратичные формы. 37 Тема 10. 39 Аналитическая геометрия на плоскости. Простейшие задачи. 39 Тема 11. 41 Кривые второго порядка. 41 Тема 12. 44 Прямая и плоскость в пространстве. 44 Тема 13. 46 Векторная алгебра. 46 Справочные материалы.. 48 ГЛОССАРИЙ.. 50 ПЕРЕЧЕНЬ УМЕНИЙ.. 54 Литература. 58
Учебно-методическое пособие по курсу «Высшая математика» разработано в соответствии с типовой учебной программой и преследует собой – устранить недостаточность и разрозненность задачников по данному курсу. Данное пособие предназначено для изучения следующих разделов курса: «Линейная алгебра», «Векторная алгебра», «Аналитическая геометрия». К каждой теме приведены вопросы, которые необходимо знать для изучения предложенной темы. Представлены примеры для решения студентами, как на практических занятиях, так и для выполнения домашних заданий. В конце пособия приведен глоссарий к разделу «Линейная алгебра» и справочный материал по теме «Векторная алгебра». Тема 1 Матрицы I. Контрольные вопросы. 1. Что называется матрицей? 2. Что понимается под операцией транспонирования матрицы? Существует ли транспонированная матрица для матрицы 3. Свойства операции транспонирования матриц
4. Записать в развернутом виде матрицу 5. Можно ли сложить две матрицы с размерами 6. Как перемножаются матрицы? Можно ли умножить матрицу с размерами 7. Как связаны между собой минор и алгебраическое дополнение элемента Примеры решения задач Пример 1. Вычислить произведение матриц Решение. Перемножим матрицы, умножая элементы каждой строки на соответствующие элементы каждого столбца.
Пример 2. Доказать, что матрица Решение. Подставим матрицу
Следовательно, матрица II. Задания 1. Даны матрицы
2. Найти значение многочлена
3. Как изменится произведение а) переставить б) к в) переставить г) к 4. Найдите те из произведений матриц
5. Вычислить
6. Какие из следующих операций можно провести с матрицами А, В?
7. Является ли матрица Тема 2 Свойства определителей I. Контрольные вопросы. 1. Что значить разложить определитель по элементам строки (столбца). 2. Запишите схематично «правило треугольника». 3. Запишите теорему Лапласа. 4. Сформулируйте свойства определителя и на примере определителя 3-го порядка, написанного в общем виде докажите их. Примеры решения задач Пример 1. Вычислит величину определителя Решение. Рассмотрим три способа нахождения величины определителя. 1 способ основан на разложении определителя (теорема Лапласа), например, по первой строке. 2 способ использует правило треугольников (правило Саррюса).
3 способ основан на приведении определителя к треугольному виду. Определитель же треугольной матрицы равен произведению её диагональных элементов.
Последний способ прекрасно работает с большими определителями. II. Задания. 1. Вычислите определители 2-го порядка
2. Вычислите определитель 3-го порядка
3. Решите уравнение
4. Решите неравенство
5. Используя свойства определителя доказать следующие тождества (определители не развертывать):
6. Вычислить следующие определители используя свойства
7. Вычислить определители; получив максимальное число нулей в строке или столбце:
8. Вычислить определитель 6-го порядка, элементы которого заданы условиями 9. Вычислить определитель 6-го порядка, элементы которого заданы условиями 10. Найти значение параметра С, при котором величина определителя матрицы Тема 3 Примеры решения задач Пример 1. Для матрицы Решение. Метод присоединенной матрицы. Найдем определитель матрицы Составим присоединенную матрицу из алгебраических дополнений к элементам транспонированной. Например, Пример 2. Решить матричное уравнение, считая все матрицы, участвующие в преобразованиях, невырожденными. Решение. Воспользуемся свойствами транспонированной и обратной матриц: II. Задания. 1. При каких значениях
2. Найти 3. Решить матричные уравнения
4. Вычислить значение
5. Решить систему матричных уравнений
6. Решить матричные уравнения
Тема 4 Примеры решения задач Пример 1. Решить систему линейных уравнений 1. Методом Гаусса 2. С помощью обратной матрицы 3. Методом Крамера Решение. 1. Методом Гаусса образуем расширенную матрицу и приведем её к треугольному виду:
Получим систему: Итак, решением системы уравнений является тройка чисел 2. С помощью обратной матрицы. Представим систему уравнений в виде матричного уравнения
Решение матричного уравнения имеет вид
и найдем обратную 3. Методом Крамера. Найдем главный определитель и определители матрицы коэффициентов, у которой один из столбцов заменен на столбец свободных членов. Неизвестные находятся по формуле Крамера: II. Задания. 1. Решите по формулам Крамера и методом обратной матрицы,
2. Решите методом Гаусса.
Тема 5 Ранг матрицы СЛАУ. I. Контрольные вопросы. 1. Какая система линейных уравнений называется совместной? 2. При каких условиях система 3. Теорема Кронекера-Капелли. 4. Когда система n-линейных уравнений имеет единственное решение? 5. Как определить число базисных и свободных переменных? 6. Как найти частное решение неоднородной системы линейных уравнений? 7. Как найти все множество решений неоднородной системы линейных уравнений? 8. Что такое ранг матрицы? 9. При каких преобразованиях матрицы не меняется ее ранг? Примеры решения задач Пример 1. Найти ранг матрицы системы и решить систему
Решение. Найдем ранг расширенной матрицы системы
Минор в квадратных скобках, составленный из коэффициентов при переменных Решая её получим II. Задания. 1. Найти ранг матрицы
2. Что можно сказать о решении СЛАУ если:
3. Исследовать систему на совместность и решить ее, если она совместна.
Тема 6 Примеры решения задач Пример 1. Найти какие-либо фундаментальные решения системы уравнений: Решение. Составим матрицу из коэффициентов при неизвестных
Приведем её у диагональному виду: Это решение удобно записать в следующем виде:
Общее решение однородной системы уравнений теперь можно записать так:
Два столбца элементов II. Задания.
Тема 7 Примеры решения задач Пример 1. Являются ли векторы Решение. Составим матрицу из координат векторов, расположив, например, их в виде строк, и найдем её ранг Из трех строк только две являются линейно независимыми. Следовательно, векторы линейно зависимы. Найдем связь между ними. Запишем линейную комбинацию
Решим систему по методу Гаусса Пример 2. Пусть в некотором старом базисе заданы векторы Решение. Векторы II. Задания. 1. Найти линейную комбинацию векторов.
2. Выяснить вопрос о линейной зависимости векторов: v 1) Составить нулевую линейную комбинацию из заданных векторов с неизвестным коэффициентом 2) Записать покоординатные равенства в систему. 3) Решить систему уравнений относительно неизвестных коэффициентов. 4) Определить число ненулевых угловых коэффициентов в ступенчатой матрице, оно определяет число линейно независимых векторов в системе.
3. Является ли линейным пространством заданное множество, если множество – это множество всех векторов 3-х мерного пространства, координаты которых – целые числа, сложение векторов и умножение на число определены общепринятым способом: т.е. если
v a) Выбрать два элемента b) Выбрать три элемента
c) Найти в этом множестве нулевой элемент т.е. В этом множестве таким элементом является вектор d) Выбрать элемент e) Проверить для числа 1 выполнение равенства
f) Для чисел
g) Проверить для чисел
h) Для двух элементов множества
4. Исследовать на линейную зависимость систему векторов
v a) Составить линейную комбинацию из заданных векторов с неизвестными коэффициентами
b) Приравнять линейную комбинацию нулевому вектору
c) Записать координатные равенства в систему
d) Решить систему уравнений относительно неизвестных коэффициентов
e) Число ненулевых диагональных элементов в ступенчатой матрице определяет число линейно независимых векторов в системе. В ступенчатой матрице 2 ненулевых диагональных элемента 5. Исследовать на линейную зависимость систему векторов
6. Разложить вектор
7. Найти связь координат одного и того же вектора в различных базисах
8. Вектор
Тема 8 Линейные операторы. I. Контрольные вопросы. 1. Определение оператора. Пусть каждому вектору 2. Какой оператор является линейным? v
3. Запишите преобразование матрицы линейного оператора при переходе от старого базиса к новому v 4. Собственные векторы и собственное значение линейного оператора. v Вектор v Число II. Задания. 1. Найти собственные числа и собственные векторы матрицы.
2. Матрица
Тема 9 Квадратичные формы. I. Контрольные вопросы. 1. Определение квадратичной формы v Выражение вида 2. Запишите квадратичную форму в матричном виде v 3. В каком случае квадратичная форма называется канонической? 4. Критерии оценки знакоопределенности квадратичной формы Название формы |
Обозначение |
Тема 10 Тема 11 Кривые второго порядка. I. Контрольные вопросы. 1. Запишите общее уравнение кривых второго порядка. 2. Запишите канонические уравнения эллипса, гиперболы и параболы. 3. Как связаны параметры a , b , c у кривых второго порядка? 4. Что такое эксцентриситет кривых? 5. Свойство фокальных расстояний кривых второго порядка. II. Задания. 1. Составить уравнение окружности, проходящей через точки Ответ:
2. Найти значение a, при котором окружность Ответ: 3. Определить эксцентриситет эллипса, если его большая ось втрое больше малой? Ответ: 4. Составить каноническое уравнение эллипса, если его большая полуось равна 12, а эксцентриситет равен 0,8. Найти расстояние между фокусами. Ответ: 5. Эллипс проходит через точки. Составить уравнение эллипса и найти расстояние от точки Ответ: 6. Составить каноническое уравнение гиперболы 7. Составить каноническое уравнение гиперболы, проходящей через точки Ответ: 8. Дан эллипс Ответ: 9. Составить уравнение параболы и её директрисы, если известно, что парабола проходит через точки пересечения прямой Ответ: 10. Уравнение 11. На гиперболе 12. Найти стороны прямоугольника максимальной площади, вписанного в эллипс 13. Записать уравнения касательных к эллипсу 14. Найти точки пересечения эллипса Тема 12 Тема 13 Векторная алгебра. I. Контрольные вопросы. 1. Как задаются координаты вектора? 2. Как вычисляется длина вектора? 3. Когда векторы коллинеарны? 4. Запишите скалярное произведение векторов. 5. Свойства скалярного произведения векторов. 6. Что называется векторным произведением векторов? 7. Как используется векторное произведение при решении задач по геометрии? II. Задания. Векторная алгебра 1. По заданной паре векторов 2. При каких значениях параметров 3. Найдите длины векторов 4. Найдите координаты вектора 5. Какой угол составляет вектор 6. При каких значениях 7. Найти угол между диагоналями четырехугольника с вершинами 8. Векторы 9. При каких значениях параметра 10. Найти вектор Справочные материалы ГЛОССАРИЙ | ||||||
| № п/п |
Новые понятия | Содержание | ||||||
| 1 |
Линейное пространство | множество V элементов произвольной природы, в котором определены операции сложения 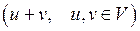 и умножения на число и умножения на число  , подчиняющиеся определенным аксиомам , подчиняющиеся определенным аксиомам
| ||||||
| 2 | Коммутативность сложения векторов | свойство операции сложения | ||||||
| 3 | Ассоциативность сложения векторов | свойство операции сложения: | ||||||
| 4 | Пространство непрерывных функций на отрезке 
| совокупность функций, непрерывных на отрезке  , с обычными операциями сложения функций и умножения функции на число; обозначается , с обычными операциями сложения функций и умножения функции на число; обозначается 
| ||||||
| 5 | Арифметическое пространство Rn | совокупность упорядоченных наборов  действительных чисел, где определены операции сложения и умножения на число действительных чисел, где определены операции сложения и умножения на число
| ||||||
| 6 | Компоненты вектора 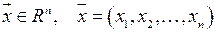
| числа | ||||||
| 7 | Вектор линейного пространства | элемент линейного пространства V | ||||||
| 8 | Линейная комбинация векторов  , принадлежащих пространству V , принадлежащих пространству V
| вектор | ||||||
| 9 | Линейно независимая система векторов | Совокупность векторов  , для которых равенство , для которых равенство  выполняется тогда и только тогда, когда числа выполняется тогда и только тогда, когда числа  . .
| ||||||
| 10 | Базис линейного пространства V | конечная система линейно независимых векторов, через которые линейно выражается любой вектор пространства | ||||||
| 11 | Линейная оболочка  системы векторов системы векторов 
| совокупность всевозможных линейных комбинаций этих векторов | ||||||
| 12 | Разложение вектора и по базису 
| это однозначное представление | ||||||
| 13 | Координаты вектора и в базисе  . .
| коэффициенты в разложении вектора по базису | ||||||
| 14 | Размерность dim V подпространства V | число векторов базиса | ||||||
| 15 | Скалярное произведение двух векторов (u,v) | скалярная функция двух векторных аргументов, подчиняющаяся определенным законам:

| ||||||
| 16 | Евклидово пространство Е | линейное пространство, в котором введено скалярное произведение | ||||||
| 17 |
Ортогональные векторы | векторы | ||||||
| 18 | Ортонормированный базис 
| базис пространства Е, для которого выполнено свойство 
| ||||||
| 19 | Неравенство Коши-Буняковского | неравенство | ||||||
| 20 |
Процесс ортогонализации | способ построения ортонормированного базиса по произвольному | ||||||
| 21 | Матрица | матрица, элементы которой  - любые векторы пространства Е - любые векторы пространства Е
| ||||||
| 22 | Линейный оператор А в линейном пространстве V | правило, по которому каждому вектору  ставится в соответствие некоторый вектор ставится в соответствие некоторый вектор  , причем , причем 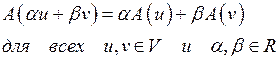
| ||||||
| 23 | Матрица А линейного оператора А в базисе 
| квадратная матрица 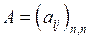 элементы которой элементы которой  определяются из соотношений определяются из соотношений 
| ||||||
| 24 | Матрица перехода от базиса  ,к базису ,к базису 
| матрица  , элементами которой , элементами которой 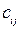 являются координаты вектора являются координаты вектора 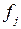 по базису по базису 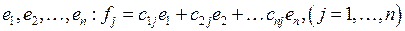
| ||||||
| 25 | Оператор  , сопряженный к оператору , сопряженный к оператору 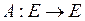
| оператор, действующий в пространстве  такой, что такой, что  для любых для любых 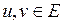
| ||||||
| 26 | Самосопряженный оператор А | такой оператор, который совпадает со своим сопряженным | ||||||
| 27 |
Симметричная матрица | матрица А, для которой At = A | ||||||
| 28 | Ортогональная матрица 
| матрица, элементы которой удовлетворяют равенству: 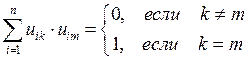
| ||||||
| 29 | Собственный вектор v оператора А | ненулевой вектор  , удовлетворяющий соотношению , удовлетворяющий соотношению 
| ||||||
| 30 | Собственное значение (собственное число), соответствующее собственному вектору v оператора А | число | ||||||
| 31 | Характеристический многочлен матрицы А | многочлен n-й степени от | ||||||
| 32 | Характеристическое уравнение | уравнение | ||||||
| 33 | Корни характеристического уравнения | множество значений  , для которых , для которых  , являются собственными значениями оператора А , являются собственными значениями оператора А
| ||||||
| 34 | Собственное подпространство, отвечающее данному собственному значению | совокупность всех собственных векторов оператора А, отвечающих данному собственному значению | ||||||
| 35 | Собственный базис самосопряженного оператора | базис из собственных векторов симметрической матрицы этого оператора | ||||||
| 36 | Линейная форма на линейном пространстве V | функция  , удовлетворяющая соотношению , удовлетворяющая соотношению 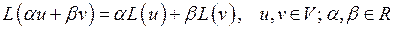 . Линейная форма может быть записана в виде: . Линейная форма может быть записана в виде:  , где , где  - данный вектор - данный вектор
| ||||||
| 37 | Билинейная форма на линейном пространстве V | функция  двух векторных аргументов двух векторных аргументов  , линейная по каждому аргументу , линейная по каждому аргументу
| ||||||
| 38 |
Квадратичная форма | функция вида | ||||||
| 39 | Матрица билинейной формы  в базисе в базисе 
| матрица | ||||||
| 40 | Матрица квадратичной формы | матрица соответствующей симметричной билинейной формы | ||||||
| 41 | Координатная запись квадратичной формы Q(v) | запись квадратичной формы в виде 
| ||||||
| 42 | Канонический вид квадратичной формы Q(v) | координатная запись формы, не содержащая произведений  , т.е. содержащая лишь квадраты координат , т.е. содержащая лишь квадраты координат
| ||||||
| 43 | Положительно определенная квадратичная форма Q(v) | форма | ||||||
| 44 | Неотрицательно определенная квадратичная форма | форма | ||||||
| 45 |
Критерий Сильвестра | теорема о необходимом и достаточном условии положительной определенности квадратичной формы | ||||||
| 46 |
Закон инерции | теорема о сохранении числа положительных, отрицательных и нулевых коэффициентов в каноническом виде, не зависимо от способа приведения квадратичной формы к сумме квадратов | ||||||
| 47 |
Метод итерации | численный метод последовательного приближения к решению | ||||||
| 48 |
Гессиан | определитель n-го порядка, элементами которого являются вторые частные производные функции n переменных | ||||||
ПЕРЕЧЕНЬ УМЕНИЙ
| № п/п | Умение | Алгоритмы |
| 1 | Проведение доказательства принадлежности множества с определенными в нем операциями к линейным пространствам | 1. Выбрав два элемента a и b заданного множества, проверить выполнение закона коммутативности сложения a+ b= b+ a.
2. Выбрав три элемента a, b, c множества, проверить выполнение закона ассоциативности сложения ( a+ b)+ c= a+( b+ c).
3. Найти во множестве нулевой элемент, т.е. элемент 0 такой, что 0+ a= a.
4. Выбрав элемент a множества, найти противоположный ему элемент, т.е элемент(- a) такой, что a+(- a)=0.
5. Проверить для числа 1 выполнение равенства 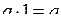 .
6. Для чисел .
6. Для чисел  проверить выполнение равенства проверить выполнение равенства  ;
7. Проверить для чисел ;
7. Проверить для чисел  выполнение равенства выполнение равенства  .
8. Для двух элементов множества .
8. Для двух элементов множества 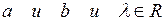 проверить выполнение равенства проверить выполнение равенства  . .
|
| 2 | Исследование системы векторов на линейную независимость | 1. Составить линейную комбинацию из заданных векторов с неизвестными коэффициентами 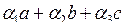 .
2. Приравнять линейную комбинацию векторов нулевому вектору.
3. Записать покоординатные равенства в систему.
4. Решить систему уравнений относительно неизвестных коэффициентов, для чего привести матрицу системы к ступенчатому виду.
5. Определить число ненулевых угловых элементов в ступенчатой матрице – оно определяет число линейно независимых векторов в рассматриваемой системе векторов. .
2. Приравнять линейную комбинацию векторов нулевому вектору.
3. Записать покоординатные равенства в систему.
4. Решить систему уравнений относительно неизвестных коэффициентов, для чего привести матрицу системы к ступенчатому виду.
5. Определить число ненулевых угловых элементов в ступенчатой матрице – оно определяет число линейно независимых векторов в рассматриваемой системе векторов.
|
| 3 | Определение размерности линейного пространства | 1. Записать матрицу А для однородной системы алгебраических уравнений. 2. Решить систему алгебраических уравнений. 3. По общему решению системы найти фундаментальную систему решений, взяв в качестве значений свободных переменных такие, чтобы матрица, составленная из них, была единичной матрицей порядка, равного числу свободных переменных. 4. Определить размерность линейного пространства решений системы, которое равно количеству векторов, образующих фундаментальную систему решений. |
| 4 | Определение координат вектора в произвольном базисе | 1. Составить матрицу перехода U от базиса b к базису e, поставив в первый столбец матрицы коэффициенты первого уравнения, во второй столбец коэффициенты второго уравнения и т.д.
2. Найти матрицу  , обратную матрице , обратную матрице  .
3. Найти координаты вектора x в базисе e, для чего вычислить произведение .
3. Найти координаты вектора x в базисе e, для чего вычислить произведение  , где x – столбец координат вектора x в базисе b, а x’ - столбец координат вектора x в базисе e.
4. Записать вектор x в базисе , где x – столбец координат вектора x в базисе b, а x’ - столбец координат вектора x в базисе e.
4. Записать вектор x в базисе 
|
| 5 | Преобразование матрицы линейного оператора при переходе к другому базису | 1. Составить матрицу перехода U от базиса e к базису b, поставив в первый столбец матрицы коэффициенты первого уравнения, во второй столбец коэффициенты второго уравнения и т.д.
2. Найти матрицу  , обратную матрице , обратную матрице  .
3. Найти произведение матриц .
3. Найти произведение матриц  .
4. Найти произведение матриц .
4. Найти произведение матриц  равное матрице оператора A в базисе b. равное матрице оператора A в базисе b.
|
| 6 | Вычисление собственных значений и собственных векторов матрицы | 1. Составить характеристический многочлен  для матрицы для матрицы  линейного оператора А.
2. Получить характеристическое уравнение оператора А, для чего приравнять характеристический многочлен нулю.
3. Найти корни характеристического уравнения, разрешив его относительно неизвестного линейного оператора А.
2. Получить характеристическое уравнение оператора А, для чего приравнять характеристический многочлен нулю.
3. Найти корни характеристического уравнения, разрешив его относительно неизвестного  , полученные корни – собственные значения линейного оператора.
4. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению , полученные корни – собственные значения линейного оператора.
4. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению  .
5. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
6. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению .
5. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
6. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению  7. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
8. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению
7. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
8. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению  9. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
9. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
|
| 7 | Построение ортогонального базиса по заданному | 1. Составить матрицу А из координат векторов  , записав в первый столбец матрицы координаты вектора , записав в первый столбец матрицы координаты вектора  , во второй – координаты вектора , во второй – координаты вектора  , а в третий координаты вектора , а в третий координаты вектора  .
2. Вычислить определитель матрицы .
2. Вычислить определитель матрицы  .
3. Если матрица А удовлетворяет условию .
3. Если матрица А удовлетворяет условию  , то заданная система векторов образует базис в , то заданная система векторов образует базис в  и может быть взята за исходную для построения ортонормированного базиса. В противном случае заданную систему векторов использовать для построения ортонормированного базиса нельзя.
4. Вычислить векторы и может быть взята за исходную для построения ортонормированного базиса. В противном случае заданную систему векторов использовать для построения ортонормированного базиса нельзя.
4. Вычислить векторы  5. Вычислить векторы
5. Вычислить векторы 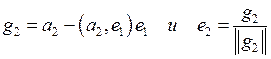 6. Вычислить векторы
6. Вычислить векторы 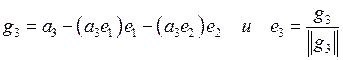
|
| 8 | Приведение квадратичной формы к каноническому виду методом выделения квадратов | 1. Сгруппировать члены квадратичной формы, содержащей квадрат переменной х и её произведение на какую-либо другую переменную, квадрат переменной у и её произведение на переменную, отличную от х. 2. Дополнить каждое из выражений, стоящих в скобках, до полного квадрата, вычитая из всего уравнения дополнительно прибавленные члены, чтобы оно не изменилось по сравнению с исходным видом квадратичной формы. 3. Записать квадратичную форму в виде суммы квадратов, получившихся в результате преобразований. 4. Перейти к новым координатам; заменив каждое из выражений, возводимое в квадрат, на новую координату, получить канонический вид записи квадратичной формы. |
| 9 | Приведение квадратичной формы к каноническому виду ортогональным преобразованием | 1. Составит матрицу квадратичной формы. 2. Составить характеристическое уравнение для матрицы А и найти его корни (собственное значение квадратичной формы). 3. Найти канонический вид квадратичной формы. 4. Найти собственные векторы, соответствующие собственным значениям. 5. Пронормировать собственные векторы. 6. Составить из столбцов координат прнормированных собственных векторов матрицу ортонормированного преобразования, приводящего квадратичную форму к каноническому виду. |
Литература
1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979.
2. Беклемешев Д.В. Линейная алгебра. – М.: Наука, 1980.
3. Воеводин В.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1984.
4. Гельфанд И.М. Лекции по линейной алгебре. – М., 1971.
5. Икрамов Х.Д. Задачник по линейной алгебре. – М., 1975.
6. Ильин В.А., Поздняк Э.Г. Линейная алгебра. – М., 1974.
7. Курош А.Г. Курс высшей алгебры. М: Физматгиз, 1962.
8. Мальцев А.И. Основы линейной алгебра. М.: Наука, 1970.
9. Проскуряков И.В. Сборник задач по линейной алгебре. М.: Наука, 1978.
10. Тышкевич В.И., Феденко А.С. Линейная алгебра и аналитическая геометрия. Минск: Вышэйша школа, 1968.
11. Фаддеев Д.К. Лекции по линейной алгебре. М.: Наука, 1984.
ВЫСШАЯ МАТЕМАТИКА.
Раздел «Линейная алгебра»
Электронное учебно-методическое пособие
для студентов 1 курса экономического факультета
Федеральное агентство по образованию
ГОУ ВПО «Кемеровский государственный университет»
Последнее изменение этой страницы: 2019-04-10; Просмотров: 292; Нарушение авторского права страницы