Вывод уравнения колебаний струны, постановка задач

Е.А.Рыбакина

НАЧАЛЬНО-КРАЕВЫЕ

ЗАДАЧИ

МАТЕМАТИЧЕСКОЙ ФИЗИКИ

 

Министерство образования и науки Российской Федерации

Балтийский государственный технический университет “Военмех”

 

Е.А.Рыбакина

НАЧАЛЬНО-КРАЕВЫЕ

ЗАДАЧИ

 МАТЕМАТИЧЕСКОЙ ФИЗИКИ

 

 

Учебное пособие

 

 

Санкт-Петербург

2005

УДК(51:53+517.927.2)(075.8)

    Р93

 

Рыбакина Е.А.

Начально краевые задачи математической физики: учебное пособие / Е.А.Рыбакина; Балт.гос.техн.ун-т.              СПб., 2005. 49 с.

 

Пособие соответствует курсу «Методы математической физики», который читается для специальностей «Приборы и системы лучевой энергетики» и «Триботехника». В нем рассмотрены начально-краевые задачи для дифференциальных уравнений в частных производных, возникающие при изучении различных физических проблем. Излагаются основные методы решения таких задач, дается физическая интерпретация решений. Теоретические сведения сопровождаются упражнениями, в конце пособия приведены задачи для самостоятельного  решения.

Предназначено для студентов инженерно-физических специальностей технических вузов.

 

УДК(51:53+517.927.2)(075.8)

 

Рецензент: зав.каф. прикладной математики и информатики БГТУ д-р физ.-мат. наук, проф. С.Д.Шапорев

 

Утверждено

редакционно-издательским

советом университета

 

 

© Е.А.Рыбакина, 2005

                                                                    © БГТУ, 2005

Введение

Современная математическая физика представляет собой довольно обширную научную область. Данный курс лекций в основном ограничивается той ее частью, которая связана с решением дифференциальных уравнений в частных производных, иначе их называют уравнениями математической физики. Различные области физики, описывающие совершенно несхожие по своей физической сущности явления, используют один и тот же математический аппарат – аппарат дифференциальных уравнений в частных производных. Математические вопросы оказываются почти одинаковыми, изучаем ли мы сигнал радара, распространение звуковой волны в жидкости или поле бесспиновых частиц. Таково удивительное свойство природы, некое математическое единство различных ее проявлений.

Курс уравнений с частными производными существенно отличается от курса обыкновенных дифференциальных уравнений тем, что в нем изучаются далеко не все уравнения, которые можно написать, используя значки  и т.п. Общей теории дифференциальных уравнений в частных производных не существует. Мы ограничимся совсем немногочисленными конкретными примерами уравнений, но выбор этих примеров не случаен – это типичные представители задач, возникающих при изучении явлений природы. Нужно сразу запомнить, что уравнения, различающиеся, на первый взгляд, совсем несущественно, могут обладать очень разными свойствами и для них будут естественными разные задачи.

Таким образом, наша цель – рассмотреть основные физические ситуации, выяснить, к каким математическим задачам они приводят, решить эти задачи и исследовать физические следствия полученных решений. Наши рассуждения при этом не всегда будут строгими с точки зрения математика, мы будем оставаться на физическом уровне строгости и только постараемся отмечать пробелы в наших рассуждениях.

В настоящем пособии подробно рассматриваются постановка физических задач и различные методы их решения для случая одномерного пространства, когда независимыми переменными в уравнениях являются время t и одна пространственная переменная x. Волновое уравнение в этом случае переходит в уравнение струны. Такое упрощение значительно сокращает математические выкладки и позволяет сосредоточиться на смысловой стороне проблемы.

Для сокращения записи в дальнейшем используются следующие аббревиатуры: ДУ – дифференциальное уравнение, ОДУ – обыкновенное дифференциальное уравнение, НКЗ – начально-краевая задача, КЗ – краевая задача, НУ – начальные условия, ГУ – граничные условия, с/ф – собственные функции, с/з – собственные значения. Частные производные, как правило, обозначаются нижними индексами, например: , , .

В тексте пособия содержатся упражнения, выполнение которых обязательно для понимания темы. В заключительной части помещены задачи для практических занятий и самостоятельного решения.

Пособие предназначено для студентов III курса, владеющих аппаратом дифференциального и интегрального исчисления, обыкновенными дифференциальными уравнениями, а также знакомых с курсом общей физики.

Корректность задач математической физики. Пример некорректной задачи

Поскольку задачи матфизики описывают реальные процессы в природе, они должны удовлетворять некоторым требованиям.

Определение . Математическая задача поставлена корректно, если

− решение задачи существует;

− задача имеет единственное решение;

− решение задачи устойчиво, т.е. оно непрерывно зависит от исходных данных.

Требование устойчивости означает, что всякий физически определенный процесс должен непрерывно зависеть от начальных и граничных условий и от неоднородного члена в уравнении, т.е. должен характеризоваться функциями, которые мало меняются при малых изменениях исходных данных. В противном случае, например, двум системам практически одинаковых НУ (различие которых лежит в пределах точности измерений) могли бы соответствовать существенно разные процессы. Такие процессы не являются физически определенными. Устойчивость важна также для приближенного решения задач.

Математическую формулировку требования устойчивости покажем на примере задачи Коши (17), попутно докажем, что она устойчива.

Утверждение. Для любого промежутка времени  и любого  найдется такое , что всякие два решения уравнения (3)  и  в течение промежутка  будут различаться меньше чем на :

,

если только НУ различаются меньше чем на :

и   ,

.

Для доказательства используем формулу Даламбера (19):

и положим .

Пример Адамара* – пример некорректной задачи. Рассмотрим задачу Коши для уравнения Лапласа**:

Функции ;  (n – параметр) удовлетворяют уравнению Лапласа и начальным условиям:

.

Для любого  при достаточно большом n разность НУ окажется меньше . При этом для любого заданного  значения  могут быть сколь угодно большими, так как. они растут с ростом n .

Задачи

Постановка начально-краевых задач

В задачах 1 − 13 описаны некоторые физические процессы. Следует выбрать функцию, характеризующую указанный процесс, вывести для нее дифференциальное уравнение, сформулировать для этой функции начальные и граничные условия. Все необходимые параметры системы предполагаются известными.

1. Сформулировать задачу о продольных колебаниях однородного упругого стержня постоянного сечения S длины l при произвольных начальных отклонении и скорости. Рассмотреть следующие случаи:

а) к концам нерастянутого стержня  и , начиная с момента  приложены силы  и , действующие вдоль стержня;

б) концы стержня закреплены упруго, т.е. на них действуют силы, пропорциональные их отклонению;

в) конец стержня  испытывает сопротивление, пропорциональное скорости, а конец  закреплен жестко;

г) конец стержня  закреплен, а конец  свободен и к нему прикреплена точечная масса m;

д) стержень закреплен на конце  и растянут силой F, приложенной к другому концу; в момент  действие силы внезапно прекращается;

е) стержень (на единицу длины) испытывает действие пропорциональной скорости силы сопротивления отклонению, а концы стержня двигаются по заданным законам  и ;

ж) начиная с момента , стержень испытывает действие направленной вдоль оси x силы объемной плотности , а концы стержня свободны. (Такую силу можно создать, например, с помощью магнитного поля.)

2. Начиная с момента , один конец прямолинейного упругого однородного стержня совершает продольные колебания по заданному закону, а к другому концу приложена сила , направленная по оси стержня. В момент  стержень был неподвижен и находился в равновесном положении. Поставить задачу для определения его малых продольных колебаний.

3. Сформулировать задачу о продольных колебаниях однородного упругого стержня переменного сечения  длины l при произвольных начальных отклонении и скорости для случая, когда стержень имеет форму усеченного конуса с радиусами оснований r и R , причем основания закреплены жестко.

4. Сформулировать задачу о продольных колебаниях однородного упругого стержня переменного сечения  длины l при произвольных начальных отклонении и скорости для случая, когда конец стержня  закреплен упруго, а к концу , начиная с момента , приложена продольная сила  на единицу площади сечения.

5. Поставить задачу о малых поперечных колебаниях струны в среде с сопротивлением, пропорциональным скорости, предполагая, что

а) концы струны закреплены жестко;

б) один конец свободен, а на другой действует переменная поперечная сила .

6. Однородная струна с закрепленными концами находится во внешнем поперечном магнитном поле с индукцией B. Поставить задачу о колебаниях этой струны, если по ней течет переменный ток I(t).

7. Поставить задачу о продольных колебаниях однородного упругого вертикального стержня, пренебрегая действием силы тяжести на частицы стержня, если верхний конец стержня закреплен жестко, а к нижнему концу прикреплен груз массой M, причем за начальное состояние принимается ненапряженное состояние стержня (т.е. в начальный момент времени из-под груза убирается подставка и он начинает растягивать стержень).

8. Верхний конец упругого однородного вертикально подвешенного тяжелого стержня жестко прикреплен к потолку свободно падающего лифта, который, достигнув скорости v, мгновенно останавливается. Поставить задачу о продольных колебаниях этого стержня.

9. Поставить задачу о поперечных колебаниях тяжелой однородной струны относительно вертикального положения равновесия, если ее верхний конец жестко закреплен, а нижний свободен.

10. Неоднородная струна линейной плотности  совершает поперечные колебания около горизонтального положения в поле силы тяжести. В точках  струны укреплены шарики массами . Описать движение струны при произвольных начальных условиях для случаев:

а) левый конец струны свободен, правый движется по закону ;

б) левый конец струны закреплен, к правому приложена сила .

11. Однородная струна при вращении вокруг вертикальной оси с постоянной угловой скоростью  находится в горизонтальной плоскости, причем один конец струны прикреплен к некоторой точке оси, а другой свободен. В момент  точкам струны сообщают малые вертикальные отклонения и скорости. Поставить задачу для определения отклонений точек струны от плоскости равновесного движения. Силой тяжести пренебречь.

12. Два полуограниченных упругих однородных стержня с одинаковыми поперечными сечениями S соединены торцами и составляют один неограниченный стержень. Пусть  и  - плотность и модуль упругости одного из них, а  и  - другого. Поставить задачу для определения отклонений сечений стержня от их положения покоя, если заданы их начальные отклонения и скорости.

13. Решить предыдущую задачу, считая, что между торцами составляющих стержней закреплена жесткая прокладка пренебрежимо малой толщины с массой m.

Решение задач о свободных колебаниях струны методом Даламбера и методом отражений

В задачах 14 − 19 указаны начальные возмущения струны при . Решить задачи о свободных колебаниях струны графически; изобразить форму струны в моменты времени , где ; найти формулы, описывающие профиль струны в эти моменты.

14. Бесконечная струна возбуждена локальным отклонением, изображенным на рис.11 (оттянута за одну из своих точек), и отпущена без начальной скорости.

 

Рис. 11

15. Бесконечной невозмущенной струне сообщена на отрезке  поперечная начальная скорость ; вне этого отрезка начальная скорость равна нулю.

16. Полубесконечная струна, закрепленная на конце , возбуждена начальным отклонением, изображенным на рис.12. Начальные скорости струны равны нулю.

Решить эту задачу для случая, когда конец  свободен.

 

 

 

Рис.12

17. Полубесконечной невозмущенной струне в начальный момент с помощью поперечного удара передается импульс I в малой окрестности точки x₀. Рассмотреть случаи, когда конец  закреплен или свободен.

18. В начальный момент времени струна длины l с закрепленными концами была оттянута за одну из своих внутренних точек x₀ и отпущена без начальной скорости. Рассмотреть случаи .

19. Концы струны  и  жестко закреплены, струна находится в положении равновесия. В начальный момент времени малой окрестности точки  сообщается скорость .

Решить эту задачу для случаев, когда оба конца струны свободны и когда один конец закреплен, а другой свободен.

Решение начально-краевых задач методом Фурье

В задачах 20 – 35 решение  следует представить в виде ряда Фурье, как это показано в примере 1. В некоторых частных случаях ряд может содержать конечное число слагаемых.

Пример 1. Решить I НКЗ для однородного уравнения струны:

, , ,

, , , .

Решение следует искать в виде суммы (50): , где  - произвольная функция, удовлетворяющая ГУ. Выберем ее линейной по x: ; подстановка в ГУ дает

;  ; ;

окончательно .

Подставляя сумму (50) в исходную задачу, получаем НКЗ для функции :

,  ,   ,

, .

Видно, что  удовлетворяет неоднородному уравнению с нулевыми ГУ и неоднородными НУ. Решение такой задачи построено в § 7, его следует искать в виде суммы , где  удовлетворяет однородному уравнению с ненулевыми НУ,  - неоднородному уравнению с нулевыми НУ:

, ,  , ;

, , .

Обе функции  и  определяются в виде рядов Фурье по  (в нашей задаче ). Выпишем разложения в ряды Фурье по синусам на промежутке  для входящих в задачу функций:

;    .

Ряд Фурье для функции  имеет вид (42) (в задаче ):

;

подстановка его в начальные условия дает

;   ,

следовательно, , , .

Функция  задается рядом (45): , подставляя его в уравнение и НУ, получаем

,

следовательно,

; , .

Общее решение этого уравнения

;

из начальных условий следует: ;  

и окончательно .

Таким образом, получены разложения в ряды для решений  и ; суммируя их и , приходим к окончательному ответу:

Прямой выкладкой нетрудно проверить, что полученный ряд удовлетворяет всем условиям поставленной задачи.

Пример 2. Решить смешанную НКЗ для неоднородного уравнения:

Решение будем искать в виде суммы (50): , где функция  удовлетворяет ГУ задачи. Ее можно выбрать линейной: ; подстановка в граничные условия дает равенства , , следовательно, ,  и окончательно получаем .

Для функции  возникает следующая НКЗ с нулевыми ГУ:

Решение смешанной НКЗ в виде ряда Фурье предлагалось построить в упражнении 12. Повторяя рассуждения § 6, разделим переменные, т.е. будем искать решение соответствующего однородного уравнения  в виде произведения функций (40): . Подстановка произведения в однородное уравнение приводит к равенству , из которого, с учетом ГУ задачи, выводится следующая КЗ для X(x): .

Нетрудно получить набор собственных функций и собственных значений этой задачи:

, , .

Решение как однородного, так и неоднородного уравнений следует искать в виде рядов Фурье по :

.

Подстановка ряда в уравнение и НУ дает равенства

; .

 является первым членом ряда Фурье по  при , поэтому, приравнивая коэффициенты Фурье, мы получаем различные задачи для  и :

;

Вторая задача имеет только тривиальное решение: , следовательно, ряд для функции  состоит из одного первого слагаемого. Общее решение уравнения для : , с учетом НУ получаем

.

Для функции  имеем ;

ответ исходной задачи:

.

Решение этой задачи можно было несколько сократить. Установив, что функция  представима рядом Фурье по , и заметив, что все входящие в задачу функции содержат только один член  этого ряда, можно было сразу искать  в виде произведения: .

Пример 3. Решить вторую НКЗ для однородного уравнения струны:

Решение задачи будем искать в виде суммы (50): , при этом попытаемся подобрать функцию , одновременно удовлетворяющую уравнению и ГУ; обычно это удается, если в задаче фигурируют const, exp, sin, cos. Функцию  будем искать в виде , где , . Подстановка в уравнение дает , для  получаем уравнение .Его общее решение имеет вид , из начальных условий следует, что . В результате получаем

и .

Подставим сумму  в исходную задачу:

Для функции   возникла задача из однородного волнового

 

уравнения с однородными НУ и ГУ, которая имеет только тривиальное решение: . Ответ исходной задачи:

.

Отметим, что в общем случае при таком методе решения для функции  возникает задача из однородного уравнения с однородными граничными и неоднородными начальными условиями. Для граничных условий II рода ее решение следует искать в виде ряда:

.

20. Однородная струна со свободным концом  и закрепленным концом  имеет в начальный момент форму квадратичной параболы: . Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.

21. Однородная струна, закрепленная на конце  и свободная на конце , находится в прямолинейном положении равновесия. В момент времени  она получает в точке x ₀ удар от молоточка, который сообщает этой точке скорость v _0. Описать свободные колебания струны. Молоточек считать плоским, шириной :

22. Однородная струна, свободная на конце  и закрепленная на конце , находится в прямолинейном положении равновесия. В момент времени  она получает в точке x ₀ удар от молоточка, который сообщает этой точке скорость v _0. Описать свободные колебания струны. Молоточек считать выпуклым, шириной :

23. Описать продольные колебания цилиндрического стержня, один конец которого свободен, а к другому с момента  приложена сила , направление которой совпадает с осью стержня. (Считать, что  не совпадает с собственными частотами стержня.)

24. На струну длиной l действует внешняя возмущающая сила, плотность которой равна  (  не совпадает с собственными частотами струны). Найти закон колебаний струны, если начальные отклонения и скорости равны нулю, левый конец струны закреплен, а правый свободен.

В задачах 25 – 28 функция  определена при , .

25. , , , , .

26. , , , , .

27. , , , .

28. , , , .

В задачах 29–32 функция  определена при , .

29. , , .

30. , , .

31.                 ,

, , , .

32.             ,

, , , .

В задачах 33–35 функция  определена при , .

33.             ,

, , , .

34.                 ,

, , , .

35.                    ,

                , , .

Для домашних заданий удобно использовать богатый набор однотипных нетрудных задач из сборника [5], глава XI. Задачи для уравнения свободных колебаний струны с однородными ГУ полезно решать двумя способами: методом отражений и методом Фурье и сравнивать результаты.

Библиографический список

1. Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям математической физики. 2-е изд. М., 1985.

2. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. 3-е изд. М., 1980.

3. Владимиров В.С. и др. Сборник задач по уравнениям математической физики. М., 2003.

4. Гюнтер Н.М., Кузьмин Р.О. Сборник задач по высшей математике. 13-е изд. СПб., М., 2003.

5. Кузнецов Л.А. Сборник заданий по высшей математике. М., 1994.

6. Очан Ю.С. Сборник задач по методам математической физики. 2-е изд. М., 1973.

7. Смирнов В.И. Курс высшей математики. Т.2. 21-е изд. М., 1974.

8. Смирнов М.М. Задачи по уравнениям математической физики. 6-е изд. М., 1975.

9. Тихонов А.Н., Самарский А.А. Уравнения математической физики. 5-е изд. М., 1977.

 

 

 

О г л а в л е н и е

 

Введение. 3

§1. Вывод уравнения колебаний струны, постановка задач. 4

§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера 11

§3. Корректность задач математической физики. Пример некорректной задачи. 17

§4. Свободные колебания полубесконечной струны. Метод отражений  (метод продолжений) 18

§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений) 23

§6. Свободные колебания ограниченной струны. Метод  Фурье (метод разделения переменных) 28

§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных) 33

Задачи. 38

Постановка начально-краевых задач. 38

Решение задач о свободных колебаниях струны методом Даламбера и методом отражений 40

Решение начально-краевых задач методом Фурье. 41

Библиографический список. 48

 

Рыбакина Елена Альбертовна

Начально-краевые задачи

Математической физики

Редактор Г.М.Звягина

Подписано в печать 07.06.2005. Формат бумаги 60х84/16. Бумага документная.

Печать трафаретная. Усл. печ.л. 3. Тираж 150 экз. Заказ №           

Балтийский государственный технический университет

Типография БГТУ

190005, С-Петербург, 1-я Красноармейская ул., д.1

*Исаак Ньютон (1643-1727) – английский физик, математик, астроном.

*Огюстен Луи Коши (1789-1857) – французский математик.

*Роберт Гук (1635-1703) – английский ученый.

* Томас Юнг (1773-1829) – английский ученый.

** Жан Д’Аламбер (1717-1783) – французский математик и механик.

* Христиан Гюйгенс (1629-1695) – нидерландский ученый.

* Жак Адамар (1865-1963) − французский математик.

** Пьер Лаплас (1749-1827) − французский математик, физик, астроном

* Жан Батист Фурье (1768-1830) − французский математик и физик.

* Жак Шарль Штурм (1803-1855) – французский математик.

Жозеф Лиувилль (1809-1882) − французский математик

* Жозеф Луи Лагранж (1736-1813) − французский математик и механик.

Е.А.Рыбакина

НАЧАЛЬНО-КРАЕВЫЕ

ЗАДАЧИ

МАТЕМАТИЧЕСКОЙ ФИЗИКИ

 

Министерство образования и науки Российской Федерации

Балтийский государственный технический университет “Военмех”

 

Е.А.Рыбакина

НАЧАЛЬНО-КРАЕВЫЕ

ЗАДАЧИ

 МАТЕМАТИЧЕСКОЙ ФИЗИКИ

 

 

Учебное пособие

 

 

Санкт-Петербург

2005

УДК(51:53+517.927.2)(075.8)

    Р93

 

Рыбакина Е.А.

Начально краевые задачи математической физики: учебное пособие / Е.А.Рыбакина; Балт.гос.техн.ун-т.              СПб., 2005. 49 с.

 

Пособие соответствует курсу «Методы математической физики», который читается для специальностей «Приборы и системы лучевой энергетики» и «Триботехника». В нем рассмотрены начально-краевые задачи для дифференциальных уравнений в частных производных, возникающие при изучении различных физических проблем. Излагаются основные методы решения таких задач, дается физическая интерпретация решений. Теоретические сведения сопровождаются упражнениями, в конце пособия приведены задачи для самостоятельного  решения.

Предназначено для студентов инженерно-физических специальностей технических вузов.

 

УДК(51:53+517.927.2)(075.8)

 

Рецензент: зав.каф. прикладной математики и информатики БГТУ д-р физ.-мат. наук, проф. С.Д.Шапорев

 

Утверждено

редакционно-издательским

советом университета

 

 

© Е.А.Рыбакина, 2005

                                                                    © БГТУ, 2005

Введение

Современная математическая физика представляет собой довольно обширную научную область. Данный курс лекций в основном ограничивается той ее частью, которая связана с решением дифференциальных уравнений в частных производных, иначе их называют уравнениями математической физики. Различные области физики, описывающие совершенно несхожие по своей физической сущности явления, используют один и тот же математический аппарат – аппарат дифференциальных уравнений в частных производных. Математические вопросы оказываются почти одинаковыми, изучаем ли мы сигнал радара, распространение звуковой волны в жидкости или поле бесспиновых частиц. Таково удивительное свойство природы, некое математическое единство различных ее проявлений.

Курс уравнений с частными производными существенно отличается от курса обыкновенных дифференциальных уравнений тем, что в нем изучаются далеко не все уравнения, которые можно написать, используя значки  и т.п. Общей теории дифференциальных уравнений в частных производных не существует. Мы ограничимся совсем немногочисленными конкретными примерами уравнений, но выбор этих примеров не случаен – это типичные представители задач, возникающих при изучении явлений природы. Нужно сразу запомнить, что уравнения, различающиеся, на первый взгляд, совсем несущественно, могут обладать очень разными свойствами и для них будут естественными разные задачи.

Таким образом, наша цель – рассмотреть основные физические ситуации, выяснить, к каким математическим задачам они приводят, решить эти задачи и исследовать физические следствия полученных решений. Наши рассуждения при этом не всегда будут строгими с точки зрения математика, мы будем оставаться на физическом уровне строгости и только постараемся отмечать пробелы в наших рассуждениях.

В настоящем пособии подробно рассматриваются постановка физических задач и различные методы их решения для случая одномерного пространства, когда независимыми переменными в уравнениях являются время t и одна пространственная переменная x. Волновое уравнение в этом случае переходит в уравнение струны. Такое упрощение значительно сокращает математические выкладки и позволяет сосредоточиться на смысловой стороне проблемы.

Для сокращения записи в дальнейшем используются следующие аббревиатуры: ДУ – дифференциальное уравнение, ОДУ – обыкновенное дифференциальное уравнение, НКЗ – начально-краевая задача, КЗ – краевая задача, НУ – начальные условия, ГУ – граничные условия, с/ф – собственные функции, с/з – собственные значения. Частные производные, как правило, обозначаются нижними индексами, например: , , .

В тексте пособия содержатся упражнения, выполнение которых обязательно для понимания темы. В заключительной части помещены задачи для практических занятий и самостоятельного решения.

Пособие предназначено для студентов III курса, владеющих аппаратом дифференциального и интегрального исчисления, обыкновенными дифференциальными уравнениями, а также знакомых с курсом общей физики.

Вывод уравнения колебаний струны, постановка задач

Вывод уравнения. Струна – гибкая тонкая нить или проволока (струна фортепиано, скрипки, арфы). Будем считать, что она находится под действием сильного натяжения T₀ и в состоянии равновесия без внешнего воздействия вытянута вдоль оси x. Если вывести струну из положения равновесия или подвергнуть действию внешней силы, она начнет колебаться, произвольная точка A в момент t займет положение 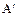 (рис. 1). Будем рассматривать только малые поперечные колебания струны и считать, что они происходят в одной плоскости, т.е. все точки струны движутся вдоль оси y. Описать движение струны − значит задать функцию .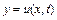

Рис.1

Обозначим через  линейную плотность внешней силы,  − линейную плотность струны, , здесь dm – масса элемента dx. Выделим произвольный кусочек струны, который в равновесии располагался между точкой A с координатой x и точкой B с координатой x + dx (рис. 2), и выпишем для него второй закон Ньютона*. Проекция суммы сил на ось y равна: . Благодаря малости колебаний жесткостью струны можно пренебречь и считать натяжение T₀ постоянным, кроме того, , , в результате проекция суммарной силы равна:

.

Ускорение выделенного кусочка u_tt, его масса , следовательно,

.                        (1)

Мы получили уравнение малых вынужденных поперечных колебаний струны в общем случае. Уравнение (1) – линейное неоднородное ДУ второго порядка с переменными коэффициентами.

  

 

Рис.2

Если струна однородна, , то, обозначив , , получим ДУ с постоянными коэффициентами

.                               (2)

Именно его обычно называют уравнением вынужденных колебаний струны. При отсутствии внешнего воздействия, f ( x , t )=0,   приходим к уравнению свободных колебаний струны (однородному ДУ):

.                                     (3)

При выводе (2) мы предполагали, что внешняя сила распределена вдоль струны непрерывно; иногда приходится иметь дело с силой P ( t ), сосредоточенной в некоторой точке C (рис. 3). Второй закон Ньютона для элемента струны dx, содержащего точку C, имеет вид

,

причем левая часть равенства стремится к нулю при бесконечном уменьшении dx. Обозначив пределы  при стремлении x к C слева и справа, соответственно, через  и , приходим к соотношению

.                              (4)

 

Рис.3

 

Видно, что непрерывная функция u ( x , t ) имеет в точке C угловую точку, т.е. скачок производной.

Замечание. При выводе уравнений колебаний мы пренебрегали сопротивлением воздуха; если его учесть, в уравнениях появится слагаемое с первой производной , так как сила сопротивления пропорциональна скорости.

Начальные и граничные условия. ДУ с обыкновенными и, тем более, с частными производными имеют, вообще говоря, бесчисленное множество решений. При изучении ОДУ говорилось об общем решении такого уравнения, содержащем произвольные постоянные; при различных значениях этих постоянных возникают различные частные решения (возможно еще особое решение). Чтобы фиксировать конкретное решение ОДУ, надо задать дополнительные условия. Для ОДУ второго порядка это могут быть значения функции и ее первой производной в некоторой точке (задача Коши*) или значения функции в двух точках (краевая задача). Аналогично обстоит дело с ДУ в частных производных, но теперь общее решение содержит не произвольные постоянные, а произвольные функции. (Впрочем, задача построения общего решения часто и не ставится.)

Колебания ограниченной струны длины l, начавшиеся в момент времени t₀, описываются функцией u ( x , t ), где , . Концы струны могут быть закреплены в положениях равновесия (рис. 4, а), тогда на концах промежутка должны выполняться условия

;                        (5а)

если же концы струны движутся по определенным законам, условия примут вид

.               (6а)

 

а)                                                          б)

Рис.4

Свободными называют концы струны, прикрепленные к невесомым колечкам, которые без трения скользят по стержням, расположенным при x = 0 и x = l вдоль оси y (рис. 4, б). В этом случае

,                    (5б)

так как y-составляющие сил, действующих со стороны струны на колечки, должны быть равны нулю. Если к колечкам приложены внешние силы  и , (5б) заменится на

,               (6б)

где , .

Возможен также случай упруго закрепленных концов  (рис.4, в), когда к колечкам приложены упругие силы, стремящиеся вернуть концы в равновесные положения. Эти силы подчиняются закону Гука*: . Суммы упругой силы и y-составляющей силы натяжения струны на каждом конце должны обращаться в нуль, поэтому

. (5в)

Если точка упругого закрепления перемещается по определенному закону, (5в) переходит в

. (6в)

Определение . Условия на границе (5) или (6) называются граничными, краевыми или предельными; (5а) и (6а) – условия I рода, (5б) и (6б) – II рода, (5в) и (6в) − III рода. Условия (5) – однородные, (6) – неоднородные. Все перечисленные условия линейны.

Условия «б» и «в» для струны могут показаться искусственными. Но в других физических задачах, также сводящихся к уравнению струны, например при изучении продольных колебаний в стержне или распространении звука в газовой трубе, естественными оказываются как раз эти условия.

ГУ еще не задают процесс колебаний струны однозначно, нужно указать форму струны и распределение скоростей в некоторый момент времени t₀ (принимаемый за начальный):

                        (7)

– начальные условия или данные Коши.

Начальные и граничные условия вместе однозначно определяют решение уравнения струны.

Формулировка I начально-краевой задачи : найти функцию , , , удовлетворяющую:

     (8)

Аналогично ставятся II и III НКЗ. Если граничные условия при x=0 и x=l относятся к разным типам, такие задачи называются смешанными. В дальнейшем для простоты считаем, что начало отсчета времени совпадает с началом колебаний, т.е. .

Частные случаи.

1. Влияние ГУ в некоторой точке, достаточно удаленной от границ, скажется через большой промежуток времени (потом докажем это строго), следовательно, до некоторого момента времени влиянием границ можно пренебречь и рассматривать задачу для неограниченной области, так называемую задачу Коши:

            (9)

2. Если точка находится вблизи одной границы, а влиянием другой можно пренебречь, приходим к задаче на полуоси:

             (10)

3. Если начальный момент достаточно удален, его влияние в реальной системе ослабевает (благодаря трению); такая задача без начальных условий характерна при периодическом граничном режиме:

           (11)

Редукция общей задачи. Благодаря линейности уравнения и всех начальных и граничных условий можно свести решение общей НКЗ к решению нескольких более простых задач. Рассмотрим редукцию на примере I НКЗ (8).

Пусть функции , , являются решениями (8) с неоднородностями  и дополнительными условиями . Тогда имеет место суперпозиция решений, т.е. функция  удовлетворяет задаче

Как следствие, решение общей НКЗ (8) может быть представлено в виде суммы

,

где  – решения следующих частных НКЗ:

                  (12)

                          (13)

               (14)

Упражнение 1. Пусть на струну действуют постоянные во времени внешние силы с линейной плотностью F ( x ). Ее положение равновесия определится уравнением (1), в котором :

.

Найти форму однородной струны в поле силы тяжести, , если ее концы подвешены на одной высоте.

Ответ: .

Упражнение 2. Показать, что энергия механических колебаний струны с закрепленными концами равна:

,                   (15)

в частности, для однородной струны

                ( )

Упражнение 3. Вывести уравнение продольных колебаний стержня или струны:

;      (16)

здесь  – объемная плотность и  - модуль Юнга* материала стержня. Для однородного стержня, , получаем уравнение струны с другой постоянной:

.        ( )

§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера**

Построение общего решения. Функция u ( x , t ), описывающая свободные колебания бесконечной струны, должна удовлетворять уравнению (3) и НУ (7), заданным на всей вещественной оси:

           (17)

Мы построим самое общее решение уравнения (3) в такой форме, что легко будет удовлетворить начальным условиям задачи (17).

Введем новые независимые переменные

или .

Используя правило дифференцирования сложных функций, получим

;

.

Уравнение (3) в новых переменных имеет вид

      или        .

Следовательно,  не зависит от , т.е. является функцией только : . Интегрируя, получим

(постоянная при интегрировании по  может зависеть от ). Первое слагаемое является произвольной функцией , второе – произвольной функцией : . В исходных обозначениях

,                   (18)

где  и  – произвольные функции своих аргументов. Решение (18) называется решением Даламбера, это самое общее решение уравнения (3), содержащее две произвольные функции.

Оба слагаемых в (18) допускают простую физическую интерпретацию. Пусть , тогда . Если наблюдатель вышел в момент t = 0 из точки x₀ и передвигается вдоль оси x направо со скоростью c, его координата меняется по закону . Для такого наблюдателя смещение струны  остается постоянным. Следовательно, первое слагаемое  описывает возмущение, которое движется направо со скоростью c, не меняя свою форму, так называемую прямую волну (рис. 5). Второе слагаемое  дает обратную волну, которая движется со скоростью c налево. Общее решение уравнения струны возникает при наложении прямой и обратной волн.

 

 

Рис. 5

Решение задачи Коши. Подберем произвольные функции  и  так, чтобы u(x , t) удовлетворяла НУ задачи (17). Подстановка (18) в НУ дает

.

Продифференцировав первое равенство, находим  и . Интегрированием получим

, .

Поскольку , . Подставляя выражения для  и  в (18), получаем решение Даламбера задачи Коши (17):

.       (19)

Если функция  дважды непрерывно дифференцируема и функция  один раз непрерывно дифференцируема на всей вещественной оси, решение u(x , t), задаваемое формулой (19), будет иметь непрерывные первые и вторые производные. Такое решение задачи называется классическим.

Упражнение 4. Проверить прямой подстановкой, что при сформулированных выше условиях на  и , формула (19) дает решение задачи Коши (17), т.е. справедлива теорема существования.

Замечание. Поскольку всякое решение задачи Коши, если оно существует, представимо в виде (19), справедлива теорема единственности.

В реальных ситуациях начальными данными могут оказаться функции, не удовлетворяющие указанным требованиям гладкости (например, в начальный момент струна имеет форму ломаной линии). Тем не менее, разумно считать, что формула (19) все равно дает решение задачи (17), хотя u(x,t) и не имеет всюду непрерывные производные до второго порядка. Такое решение называется обобщенным. Теория обобщенных функций и строгое определение обобщенного решения выходят за рамки данного курса.

123456Следующая ⇒

Поделиться: