Косвенные методы построения функций принадлежности нечетких множеств.

Метод попарного сравнения.

           Обработка матрицы оценок, отражающих мнение эксперта об относительной принадлежности элементов множеству или степени выраженности у них свойств, формализуемого множеством. Потребуем, чтобы для всех элементов множества S выполнялось равенство .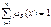

           Степень принадлежности будем определять посредством парных сравнений. Оценка элемента x_i по сравнению с x_j с точки зрения свойства   S - . Для обеспечения согласованности примем . Итак, мы имеем матрицу оценок 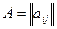. Найдем 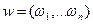собственный вектор матрицы А, решая уравнение , где l собственное значение матрицы А. Вычисленные значения  принимаются за . Т.к. всегда выполняется равенство 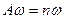, то найденные значения тем точнее, чем ближе  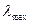к n. Отклонения  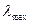от n может служить мерой согласованности суждений экспертов при составлении матрицы оценок.

Нахождение собственного вектора и собственных чисел матрицы.

Иногда приходится рассматривать уравнения типа: ,      (15.1)

где w - неизвестный числовой вектор, высота которого равна порядку , а l неизвестное число. При любом l уравнение (15.1) обладает тривиальным решением , однако нас будут интересовать только такие l, при которых эта система имеет нетривиальные решения, эти значения l называются собственными значениями матрицы А, а решения  при таких значениях - её собственными векторами. Преобразуем (15.1), используя очевидное равенство: , тогда получаем  (15.2). (15.2) представляет собой систему из n однородных алгебраических уравнений с n неизвестными. Для наличия нетривиального решения необходимо и достаточно, чтобы . Это уравнение называется характеристическим уравнением матрицы , оно служит для разыскания собственных значений l .

Раскрыв определитель, получим алгебраическое уравнение степени n (порядок матрицы А). Матрица прядка «n» имеет «n» собственных значений. Обычно выбирают максимальное по модулю значение.

           Найдя какое либо собственное значение l, мы можем соответственно собственные вектора найти из (2). Из этого уравнения вытекает, что при зафиксированной l сумма решений  будет снова решением, произведение  решения на число будет также решением уравнения. Значит, совокупность всех собственных векторов, отвечающих заданному собственному значению, образует линейное пространство (бесконечное число ненулевых решений, система обязательно зависима, т.е. одно уравнение является следствием остальных, одно из уравнений можно отбросить и задавать произвольные значения для одной из переменных). Для нахождения единственного собственного вектора используется замена одного из уравнений условием нормировки.

Пример. Оценка освещенности предмета в зависимости от расстояния до источника: предмет в 9, 15, 21 и 28 единицах длины.

Шкала для определения матрицы суждений

Оценка важности	Качественная оценка	Примечание
1	Одинаковая значимость	По данному критерию альтернативы имеют одинаковый ранг
3	Слабое превосходство	Соображения о предпочтении одной альтернативы перед другой малоубедительны
5	Сильное или существенное превосходство	Имеются надежные доказательства существенного превосходства одной альтернативы
7	Очевидное превосходство	Существуют убедительные свидетельства в пользу одной альтернативы
9	Абсолютное превосходство	В высшей степени убедительное превосходство
2,4,6,8	Промежуточные значения между соседними оценками

Эксперимент дал матрицу . Сначала находим l. Для этого составляем уравнение . Эта неоднородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы равен 0.

               

Следовательно

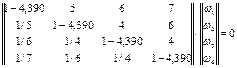
Система имеет только нулевое решение, для нахождения собственного вектора w используется замена одного из уравнений системы условием нормировки w 1 + w 2 + w 3 + w 4 =1. Решая новую систему, получаем: w 1 =0,619, w 2 =0,235, w 3 =0,101, w 4 =0,045. (степень согласованности суждений экспертов).

Билет №45

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться: