
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Виконання операцій алгебраїчного додавання в прямому кодіСтр 1 из 5Следующая ⇒
Операція Додавання Основні поняття Важливою функцією багатьох цифрових пристроїв і МП є виконання арифметичних операцій додавання і віднімання. В зв’язку з цим в ЕОМ і МП виділяють спеціальний функціональний блок – арифметичний пристрій (АП), призначений для виконання операцій над числовими кодами. Числа, які беруть участь в арифметичних операціях, називаються операндами. Для позиційних систем числення із звичайною вагою всі допустимі числа є поліномами ізстепенями р (основи системи числення). Отже, всі арифметичні діі в цьому випадку виконуються за правилами алгебраїчного додавання поліномів. Додавання у цьому випадку буде представлене в (табл.1.1) Кожна сума у таблиці 1.1 записана двома розрядами, молодший з яких є безпосередньо сума употочному ί -му розряді, а старший – цифра перенесення у наступний старший розряд Pi+1 (значення цього розряду продубльовано у останньому стовпці таблиці 1.1).
При обчисленні суми двох чисел можливі два випадки: доданки мають однакові знаки; доданки мають різні знаки. У відповідності з цим алгоритми одержання суми для кожного з варіантів значно відрізняються між собою. Так, спрощений алгоритм додавання двох чисел з однаковими знаками можна визначається таким чином: - додати два числа; - сумі присвоїти знак одного із доданків. Алгоритм одержання алгебраїчної суми можна записати таким чином: - порівняти знаки доданків і, якщо вони однакові, то виконувати додавання за першим алгоритмом; - порівняти доданки за абсолютною величиною, якщо знаки доданків різні; - якщо є необхідність, переставити числа місцями (щоб віднімати від більшого менше); - провести віднімання двох чисел; - результату присвоїти знак більшого доданку[1]. З цього випливає, що перший алгоритм значно простіший другого. Отже, бажано перетворити від’ємні числа таким чином, щоб операцію віднімання замінити додаванням, тобто виконати додавання двох чисел таким чином:
Для цього необхідно зобразити додатні та від’ємні числа єдиним натуральним кодом, що можливо досягти при використанні систем числення з додатньою основою та симетричною базою або з від’ємною основою та невід’ємною базою. При використанні однорідних позиційних систем числення з додатньою основою та невід’ємною базою натуральним кодом можна представити тільки додатні числа та нуль, тобто в цьому випадку не
Це приводить до того, що проблему представлення чисел зі знаком приходиться вирішувати на рівні слів за допомогою спеціальних кодів: прямого, оберненого та доповняльного[2].
Завдання для самоконтролю Варіант 1.
Варіант 2.
Приклад 2.
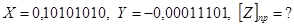 
Варіант 3.
Приклад 3. Варіант 4.
Приклад 4.
Таким чином, у прямому коді цифрову частину і знаковий розряд не можна розглдати, як єдине ціле. При цьому виконання операцій ускладнюється тим, що в структурі цифрового пристрою необхідно, крім суматора, мати ще і пристрій для віднімання кодів. Ці недоліки настільки серьозні, що прямий код для виконання операцій арифметичного додавання практично не застосовується[3].
Операція віднімання Операція віднімання проводиться подібно операції додавання чисел з фіксованою комою у цифрових обчислювальних машинах може виконуватися в одному з машинних кодів: прямому, оберненому або доповняльному. При реалізації операції віднімання знаковий розряд й інформаційна частина числа розглядаються як єдине ціле, в результаті чого з від’ємними числами машина оперує, як і з додатними. Якщо зменшуване більше від'ємника, то проблем немає, - різниця позитивна, результат вірний. Якщо зменшуване менше від'ємника, виникає проблема: результат менше 0, а це вже число зі знаком. У цьомувипадку результат необхідно загорнути. При звичайнімвирахуванні (у стовпчик) роблять позика 1 зі старшого розряду. Мікропроцесор надходить аналогічно, тобто займає 1 з розряду, що випливає за старшим, у розрядній сітці операнда. Аналогічно командам додавання група команд віднімання складається з мінімально можливого набору. Ці команди виконують віднімання по алгоритмах. Виконаємо операцію віднімання чисел, які задані у даній курсовій роботі, тобто числа «А» і «В». Нехай число «А» рівне – 6, а число «В» рівне – 4. Тоді друге число переводимо у обернений та додатковий коди:
Віднімання чисел в прямому коді Прямим кодом від’ємного числа називається його зображення в дійсні формі запису, у якого в знаковому розряді ставиться одиниця. Прямий код додатного двійкового числа співпадає з його звичайним зображенням в дійсні формі, так як знак кодується нулем. З ростом числа А його код також зростає в усій області зображення чисел. В прямому коді нуль має два значення: додатне 0, 000, … та від’ємне 1, 000, …Звичайно в ОМ використовується додатній нуль, проте в процесі обчислень може виникнути і його від’ємне зображення. Обидва значення повністю еквівалентні і застосування одного з ним не приводить до помилки[6]. Правила віднімання чисел в прямому коді не відрізняються від загальних правил віднімання. Якщо обидва числа мають однакові знаки, то вони віднімаються за загальним алгоритмом, а результату приписується знак одного з них. Якщо числа мають різні знаки, то із числових розрядів більших по абсолютні величині числа віднімається менше, а сумі приписується знак більшого числа.
Таким чином, в прямому коді знаковий розряд та цифрову частину числа не можна роздивлятись як єдине ціле, а виконання операції віднімання
Віднімання в оберненому коді Якщо знаковий розряд числа має значення (рn+1 – pk), а не pn+1, як це було в доповнювальному коді, то кількісний еквівалент числа А=азва n … an … a - k, заданий в позиційній системі додавання з основою р, буде визначатися як:
Такі коди прийнято називати оберненими, так як в них перетворення від’ємних чисел, що не потребують арифметичних операцій.
Додатні числа в оберненому коді мають таке ж зображення, як і в прямому, доповнювальному кодах Найбільша величина додатного числа знову є рn+1 – pk, що для n-розрядного двійковому дробові складатиме 1-2-n. Від’ємних чисел тепер буде на одне менше із-за неоднозначності представлення нуля. Таким чином перевага оберненого коду перед доповнювальним є простий зв'язок з прямим кодом, так як перетворення числа з прямого коду в обернений і навпаки є порозрядною операцією, що спрощує і пришвидшує перетворення числа. Особливістю оберненого коду є те, що при отримані суми, очевидно, необхідність передбачення корекцію результату, так як інверсне значення чисел відмінне від їх доповнення на одиницю молодшого розряду. В оберненому коді, як і в доповнювальному операція віднімання заміняється операцією додавання. При цьому знаковий розряді цифрова частина числа розглядається так само як одне ціле, тому машина працює з від’ємними числами як з неправильними дробами. Правильний знак суми отримується автоматично в процесі додавання цифр знакових розрядів операндів і одиниці переносу із цифрової частини, якщо вона є. Характерною особливістю оберненого коду є наявність циклічного переносу (якщо він
Віднімання в доповнювальному коді Як відомо, заміна операції віднімання на додавання основана на застосуванні деяких додаткових чисел, зв’язаних з вихідними від’ємним числами, в зв’язку з чим ці додаткові числа можна вважати вихідними, але деяким чином закодованими. Додаткові числа можуть бути знайдені, якщо знаковому розряду приписати вагу – pn+1. Величина числа А буде визначатися в цьому випадку слідуючим чином [6]:
при умові, що азв приймає значення нуль для додаткових чисел і одиниця для від’ємних. Якщо азв=0, то маємо множину додаткових чисел та нуль. Якщо ж азв=1, то всі числа від’ємні і їх абсолютна величина:
Формула (1.3) являється доповненням кількісного еквіваленту, що задається основними розрядами числа. Перетворення цифр з прямого коду в доповню вальний може бути виконане як порозрядна операція шляхом отримання в кожному розряді доповнення до р – 1 і при бавлення до перетвореного числа одиниці молодшого розряду [6].
В доповню вальному коді операція віднімання замінюється операцією алгебраїчного додавання. При цьому знаковий розряд і цифрова частина числа розглядається як єдине ціле, в результаті чого з від’ємними числами машина працює як з неправильними дробами. Правильний знак суми виходить автоматично в процесі додавання знакових розрядів операндів та одиниці переносу із цифрової частини, якщо вона є. Таким чином, у всіх
Операція множення Стосовно до двійковій системі числення найбільш відомі наступні основні способи виконання операції множення: Рис1.3-Множення двійкових чисел В обох випадках операція множення складається з ряду послідовних операцій додавання часткових добутків. Операціями додавання управляють розряди множника: якщо в якомусь розряді множника знаходиться одиниця, то до суми часткових добутків додається множене з відповідним зсувом: якщо в розряді множника - нуль, то множене не додається. Таким чином, крім операції додавання чисел для отримання добутку необхідна операція зсуву чисел. При цьому з’являється можливість
Метод 1. Нехай А – множене (А> 0), В – множник (В> 0), С – добуток. Тоді в випадку представлення чисел в формі с фіксованою крапкою отримуємо: А=0, а1а2…an; B=0; b1b2…bn=b1∙ 2-1+b2∙ 2-2+…+bn∙ 2-n. C=AB=0, а1а2…an(b1∙ 2-1+b2∙ 2-2+…+bn∙ 2-n) = (2-1∙ 0, а1а2…an)∙ b1 + + (2-2∙ 0, а1а2…an)∙ b2+…+(2n-1∙ 0, а1а2…an)bn (4.1) Множення на 2-n означає зсув на n розрядів вправо числа, що укладена в дужки, тобто в даному випадку зсувається вправо множине і множення починається зі старших розрядів. Метод 2. Нехай А=0, а1а2…an - множене і B=0; b1b2…bn – множник. Множник можна легко перетворити, використовуючи метод Горнера: В = (...((bn∙ 2-1+bn-1)2-1+…+b2)2-1+b1)2-1. Тоді С = АВ = (…((bn∙ 0, а1а2…an)2-1+bn-1∙ 0, а1а2…an)2-1+…+ + b1∙ 0, а1а2…an) 2-1
Операція ділення Ділення двійкових чисел багато в чому аналогічне діленню десяткових чисел.Процес ділення полягає в тому, що послідовно розряд за розрядом відшукуються цифри частки шляхом підбора з наступним множенням цієї цифри на дільник і відніманням цього добутку від діленого.
Насамперед це - " шкільний" алгоритм ділення, який полягає в тому, що дільник на кожному кроці віднімається стільки разів від діленого (починаючи зі старших розрядів), скільки це можливо для одержання найменшої додатної остачі. Тоді в черговий розряд частки записується цифра, яка дорівнює кількості дільників, що містяться в діленому на даному кроці. Таким чином, весь процес ділення зводиться до операцій віднімання і зсуву[7].
На відміну від множення чисел з фіксованою комою, в процесі якого принципово неможливе переповнення розрядної сітки, ділення дробових чисел може призвести до переповнення розрядної сітки і, отже, до неправильного результату. Тому для уникнення такої ситуації має виконуватись умова: Відомо два основних метода ділення чисел, а саме: ділення з відновленням та без відновлення остач. Алгоритм ділення модулів чисел з відновленням остач полягає у виконанні таких дій. П. 1. Подвоїти модуль діленого П. 2. Відняти від подвоєного модуля діленого модуль дільника. Одержана різниця П. 3. Проаналізувати знак остачі R. Якщо П. 4. Відновити остачу, додавши модуль дільника
П. 6. Визначити чергову остачу, віднявши від попередньої остачі модуль дільника. Перейти до п. 3. П. 3 - п. 6 виконувати до одержання всіх необхідних цифр частки. За своїм характером операція ділення відноситься до операцій, що дають не завжди точний результат, тому ознакою закінчення операції ділення може бути досягнення заданої точності. Якщо в процесі ділення одержується остача R = 0, то операція зупиняється й у решту розрядів частки записується нуль. Звичайно формальною ознакою кінця операції ділення є одержання такої самої кількості розрядів у частці, яку мають операнди[8]. Подвоєння діленого та остачі практично виконується шляхом зсуву коду вліво на один розряд.
Основні недоліки розглянутого методу ділення такі: · аритмічність процесу ділення, яка обумовлена нерегулярністю виконання відновлення остачі, що призводить до ускладнення блоку керування діленням; · відносно мала швидкість ділення, оскільки в середньому для половини кроків потрібно виконувати додаткове додавання, що забезпечує відновлення остач.
Висновок: В данному розділі ми розглянули логічні операції, в основному додавання в прямому, зворотньому та доповняльному кодах, з фіксованою та плаваючою комою, також операції ділення, множення і віднімання, їх принцип побудови та методи, на яких вони базуються.
Операція Додавання Основні поняття Важливою функцією багатьох цифрових пристроїв і МП є виконання арифметичних операцій додавання і віднімання. В зв’язку з цим в ЕОМ і МП виділяють спеціальний функціональний блок – арифметичний пристрій (АП), призначений для виконання операцій над числовими кодами. Числа, які беруть участь в арифметичних операціях, називаються операндами. Для позиційних систем числення із звичайною вагою всі допустимі числа є поліномами ізстепенями р (основи системи числення). Отже, всі арифметичні діі в цьому випадку виконуються за правилами алгебраїчного додавання поліномів. Додавання у цьому випадку буде представлене в (табл.1.1) Кожна сума у таблиці 1.1 записана двома розрядами, молодший з яких є безпосередньо сума употочному ί -му розряді, а старший – цифра перенесення у наступний старший розряд Pi+1 (значення цього розряду продубльовано у останньому стовпці таблиці 1.1).
При обчисленні суми двох чисел можливі два випадки: доданки мають однакові знаки; доданки мають різні знаки. У відповідності з цим алгоритми одержання суми для кожного з варіантів значно відрізняються між собою. Так, спрощений алгоритм додавання двох чисел з однаковими знаками можна визначається таким чином: - додати два числа; - сумі присвоїти знак одного із доданків. Алгоритм одержання алгебраїчної суми можна записати таким чином: - порівняти знаки доданків і, якщо вони однакові, то виконувати додавання за першим алгоритмом; - порівняти доданки за абсолютною величиною, якщо знаки доданків різні; - якщо є необхідність, переставити числа місцями (щоб віднімати від більшого менше); - провести віднімання двох чисел; - результату присвоїти знак більшого доданку[1]. З цього випливає, що перший алгоритм значно простіший другого. Отже, бажано перетворити від’ємні числа таким чином, щоб операцію віднімання замінити додаванням, тобто виконати додавання двох чисел таким чином:
Для цього необхідно зобразити додатні та від’ємні числа єдиним натуральним кодом, що можливо досягти при використанні систем числення з додатньою основою та симетричною базою або з від’ємною основою та невід’ємною базою. При використанні однорідних позиційних систем числення з додатньою основою та невід’ємною базою натуральним кодом можна представити тільки додатні числа та нуль, тобто в цьому випадку не
Це приводить до того, що проблему представлення чисел зі знаком приходиться вирішувати на рівні слів за допомогою спеціальних кодів: прямого, оберненого та доповняльного[2].
Виконання операцій алгебраїчного додавання в прямому коді Правила додавання чисел в прямому коді не відрізняються від звичайних правил додавання, наведених вище. Тобто, якщо числа мають однаковий знак, то їх числові розряди додаютьсяя, а сумі присвоюється знак одного (любого) з доданків. Якщо розряди мають різні знаки, то процедура виконання операції ускладнюється (добавляється операція порівняння модулів доданків). Після цього з числових розрядів більшого за модулем числа віднімається меньше за модулем число, а сумі присвоюється знак більшого за модулем числа. При цьому знакові розряди чисел не беруть участі у виконанні операції віднімання, оскільки вони не мають ваги. Наступні приклади ілюструють чотири основні варіанти додавання чисел у прямому коді при виконанні умови Завдання для самоконтролю Варіант 1.
Варіант 2.
Приклад 2.
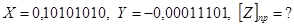 
Варіант 3.
Приклад 3. Варіант 4.
Приклад 4.
Таким чином, у прямому коді цифрову частину і знаковий розряд не можна розглдати, як єдине ціле. При цьому виконання операцій ускладнюється тим, що в структурі цифрового пристрою необхідно, крім суматора, мати ще і пристрій для віднімання кодів. Ці недоліки настільки серьозні, що прямий код для виконання операцій арифметичного додавання практично не застосовується[3].
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последнее изменение этой страницы: 2019-06-08; Просмотров: 270; Нарушение авторского права страницы