
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
По выполнению контрольной работы по теме. «Элементы операционного исчисления»Стр 1 из 6Следующая ⇒
По выполнению контрольной работы по теме «Элементы операционного исчисления» для студентов 2-3 курсов вечерне-заочного факультета
Мурманск 2015
Составитель – Хохлова Людмила Ивановна, доцент кафедры высшей математики и программного обеспечения МИС и ПО МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой _______________ 2015 г., протокол №
Рецензент – Р. А. Богомолов, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения МИС и ПО МГТУ МГТУ
Оглавление Оглавление § 1. Оригиналы. 4 § 2. Единичная функция Хэвисайда. Запись оригиналов с помощью функции Хэвисайда. 5 § 3. Преобразование Лапласа. Изображение оригинала. Основные свойства изображения. 8 §4. Применение теоремы запаздывания для нахождения изображений запаздывающих процессов. 11 §5. Изображение кусочно - непрерывных функций. 13 § 6. Применение теорем о дифференцировании оригинала и изображения для нахождения изображений. 18 § 7. Изображение интеграла от оригинала. Теорема об интегрировании оригинала. 19 § 8. Изображение периодического оригинала. 20 §9. Свертка. Изображение свертки. 23 § 10.Восстановление оригиналов по изображению. 25 П.2 Восстановление оригиналов с помощью свертки. 26 П.4. Нахождение оригиналов с помощью теоремы запаздывания. 29 § 11. Применение операционного исчисления к решению линейных дифференциальных уравнений с постоянными коэффициентами. 30 § 12. Применение операционного исчисления к решению систем линейных дифференциaльных уравнений. 32 Таблица оригиналов и изображений. 34 Таблица сверток оригиналов. 35 Образец решения контрольной работы. 38 Задания контрольной работы.. 40
Оригиналы. Определение. Оригиналом называется любая однозначная функция 1) 2) 3) Примеры. Установить какие из функций являются оригиналами и найти для них показатели роста: Замечание. Будем считать, что условие 1) выполняется для всех функций, т.к. это соответствует реальным физическим задачам. Решение. 1) 2) 3) 4) 6) 7) 8) Вопросы для самопроверки. 1. Дайте определение оригинала 2. Дайте определение показателя роста оригинала Примеры для самостоятельного решения. Установить являются ли следующие функции оригиналами: 1) Свойство линейности. Если
Свойство затухания. Если Свойство подобия. Если С помощью основных свойств преобразования Лапласа и найденного ранее изображения функции Найдем изображение константы с.
Далее воспользуемся формулами Эйлера, чтобы найти изображение остальных функций:
Используя свойства затухания и линейности получаем:
Применяя свойство затухания, получаем:
Примеры 1-4. Найти изображение следующих оригиналов
Решение. Сначала оригиналы приводим к табличному виду, а затем находим их изображения: 1) 2) 3) 4) Вопросы для самопроверки 1. Дайте определение изображения 2. Сформулируйте теорему линейности 3. Сформулируйте теорему подобия 4. Сформулируйте теорему затухания Примеры для самостоятельного решения. Найти изображения следующих оригиналов:
Вопросы для самопроверки 1. Сформулируйте теорему запаздывания. Примеры 1- 4 для самостоятельного решения. Построить графики и найти изображения следующих оригиналов:
Ответы:
Решение:
Пример 4. Найти изображение Решение:
Вопросы для самопроверки 1. Сформулируйте теорему о дифференцировании оригинала 2. Сформулируйте теорему о дифференцировании изображения Примеры 1-6 для самостоятельного решения. Найти изображение с помощью теорем о дифференцировании оригинала и изображения. 1) 2) 3) Ответы: 1) 4) Примеры 1)Найти изображение последовательности единичных прямоугольных импульсов длительности Решение. Изобразим последовательность импульсов:
Запишем оригинал и найдем изображение
2) Найти изображение “пилообразной” функции:
Решение. Запишем оригинал и найдем его изображение:
Решение.
Вопросы для самопроверки 1. Сформулируйте теорему об изображении периодического оригинала Примеры для самостоятельного решения. Найти изображения следующих периодических функций:
Ответы.1) 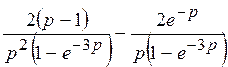 ; 2) ; 2) 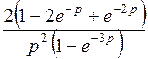 ; ;
3) 5)
Вопросы для самопроверки 1. Дайте определение свертки 2. Сформулируйте теорему об изображении свертки Примеры для самостоятельного решения. Восстановить оригиналы, используя свертку.
Ответы.
Пример 2. Найти оригинал следующего изображения: Решение. Представим
Приравниваем коэффициенты при равных степенях: A=0; C=0; B=2; D=-1.
При решении этих задач использовались теоремы единственности, линейности, затухания, таблица оригиналов и изображений. Примеры для самостоятельного решения. Найти оригинал изображения
Ответы.
Вопросы для самопроверки 1. Сформулируйте алгоритм решения дифференциального уравнения Примеры для самостоятельного решения. Решить задачу Коши.
Ответы Таблица оригиналов и изображений.
Таблица сверток оригиналов.
Решение. Найдем сначала оригинал для дроби Разложим эту дробь на простейшие и найдем коэффициенты методом неопределенных коэффициентов
При При Приравниваем коэффициенты при равных степенях:
 , применим теорему запаздывания при , применим теорему запаздывания при  . Оригинал исходного изображения f ( t ) равен . Оригинал исходного изображения f ( t ) равен 
Задача3. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Решить задачу Коши.
Решение. Пусть Изображение правой части:
Используя таблицу основных изображений, получаем, что Задача 4. Найти решение системы Решение. Пусть изображение системы имеет вид
По формулам Крамера:
Задания контрольной работы
Задача1. По данному графику оригинала найти изображение: Варианты 1-10. 1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Задача 2. Найти оригинал по заданному изображению: Варианты1-10 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задача 3. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Варианты1-10. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задача 4. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющих заданным начальным условиям. Варианты1-10. 1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Список учебной литературы
1. Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов: В 2т. Т.2/ Н.С. Пискунов. – М.: Наука, 1985. 2. Бубер, В.Б. Операционное исчисление. Опорный конспект лекций по высшей математике/ В.Б. Бубер, З.Д. Ломакина. – Мурманск, 1990. 3. Конторович, М.И. Операционное исчисление и процессы в электрических цепях/ М.И. Конторович. - М.: Сов.Радио, 1975. 4. Шелковников, Ф.А. Сборник упражнений по операционному исчислению/ Ф.А. Шелковников, К.Г. Такайшвили. – М.: Высшая школа, 1976. 5. Данко, П.Б. Высшая математика в упражнениях и задачах: В 2-х ч. Ч.2/ П.Б. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 1999.
по выполнению контрольной работы по теме «Элементы операционного исчисления» для студентов 2-3 курсов вечерне-заочного факультета
Мурманск 2015
Составитель – Хохлова Людмила Ивановна, доцент кафедры высшей математики и программного обеспечения МИС и ПО МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой _______________ 2015 г., протокол №
Рецензент – Р. А. Богомолов, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения МИС и ПО МГТУ МГТУ
Оглавление Оглавление § 1. Оригиналы. 4 § 2. Единичная функция Хэвисайда. Запись оригиналов с помощью функции Хэвисайда. 5 § 3. Преобразование Лапласа. Изображение оригинала. Основные свойства изображения. 8 §4. Применение теоремы запаздывания для нахождения изображений запаздывающих процессов. 11 §5. Изображение кусочно - непрерывных функций. 13 § 6. Применение теорем о дифференцировании оригинала и изображения для нахождения изображений. 18 § 7. Изображение интеграла от оригинала. Теорема об интегрировании оригинала. 19 § 8. Изображение периодического оригинала. 20 §9. Свертка. Изображение свертки. 23 § 10.Восстановление оригиналов по изображению. 25 П.2 Восстановление оригиналов с помощью свертки. 26 П.4. Нахождение оригиналов с помощью теоремы запаздывания. 29 § 11. Применение операционного исчисления к решению линейных дифференциальных уравнений с постоянными коэффициентами. 30 § 12. Применение операционного исчисления к решению систем линейных дифференциaльных уравнений. 32 Таблица оригиналов и изображений. 34 Таблица сверток оригиналов. 35 Образец решения контрольной работы. 38 Задания контрольной работы.. 40
Оригиналы. Определение. Оригиналом называется любая однозначная функция 1) 2) 3) Примеры. Установить какие из функций являются оригиналами и найти для них показатели роста: Замечание. Будем считать, что условие 1) выполняется для всех функций, т.к. это соответствует реальным физическим задачам. Решение. 1) 2) 3) 4) 6) 7) 8) Вопросы для самопроверки. 1. Дайте определение оригинала 2. Дайте определение показателя роста оригинала Примеры для самостоятельного решения. Установить являются ли следующие функции оригиналами: 1) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последнее изменение этой страницы: 2019-06-19; Просмотров: 153; Нарушение авторского права страницы