Нормальное уравнение прямой.

Если в общем уравнении прямой вида 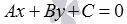числа А, В и С таковы, что длина вектора 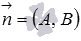равна единице, а 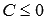, то это общее уравнение прямой называется нормальным уравнением прямой. Нормальное уравнение прямой определяет в прямоугольной системе координат Oxy прямую линию, нормальным вектором которой является вектор 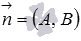, причем эта прямая проходит на расстоянии 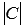от начала координат в направлении вектора .

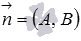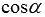Часто можно видеть другую форму записи нормального уравнения прямой: , где и 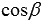- действительные числа, представляющие собой направляющие косинусы нормального вектора прямой единичной длины (то есть, 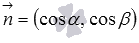и справедливо равенство 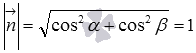), а величина p ( 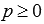) равна расстоянию от начала координат до прямой.

Для примера приведем общее уравнение прямой 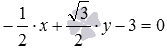. Это общее уравнение прямой является нормальным уравнением прямой, так как 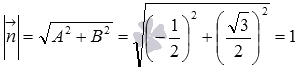и . Оно в прямоугольной системе координат Oxy на плоскости задает прямую линию, нормальный вектор которой имеет координаты 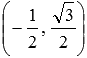, и эта прямая удаленна от начала координат на 3 единицы в направлении нормального вектора .

Отметим, что уравнение прямой в нормальном виде позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой 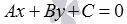числа А, В и С таковы, что уравнение 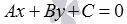не является нормальным уравнением прямой, то его можно привести к нормальному виду. Об этом читайте в статье нормальное уравнение прямой.

Кривые второго порядка

Общим уравнением второго порядка называется уравнение вида:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0

где коэффициенты A, B, C одновременно не равны нулю.
Линии, определяемые такими уравнениями, называются кривыми второго порядка.
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами.
Линии второго порядка, обладающие единственным центром, называются центральными.
Координаты центра S(x₀; y₀) линии определяются из системы:

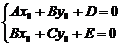
Обозначим через .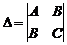
При Δ ≠ 0 кривая второго порядка будет центральной.
Причем, при Δ > 0 уравнение является уравнением эллиптического типа. Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (точка), либо мнимого эллипса (в этом случае уравнение не определяет на плоскости никакого геометрического образа).
При Δ < 0 уравнение является уравнением гиперболического типа. Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную (пару пересекающихся прямых).
При Δ =0 линия второго порядка не является центральной. Такие уравнения называются уравнениями параболического типа и определяют на плоскости либо обыкновенную параболу, либо пару параллельных (или совпадающих) прямых, либо не определяют на плоскости никакого геометрического образа
Классификация кривых второго порядка:

• Эллипс
• Окружность
• Гипербола
• Парабола

Оптические свойства кривых второго порядка:

Для эллипса: лучи света, исходящие из одного фокуса эллипса, после зеркального отражения от эллипса проходят через второй фокус.

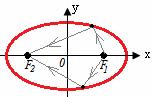
Для гиперболы: продолжение отраженного луча света, исходящего из одного фокуса гиперболы, попадает во второй фокус.

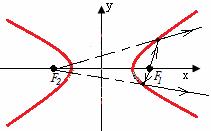
Для параболы: лучи света, исходящие из фокуса параболы, после зеркального отражения от нее образуют пучок лучей, параллельных ее фокальной оси.

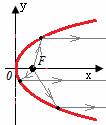
Уравнение в полярных координатах.
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы имеет вид:

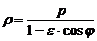
где φ, ρ - полярные координаты произвольной точки линии, p –параметр, ε - эксцентриситет. При этом полярная система координат выбрана следующим образом: полюс находится в фокусе, полярная ось направлена в сторону, противоположную ближайшей к этому фокусу директрисы.
В частности, при ε =0, получим уравнение окружности в полярных координатах:
ρ =R

 

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Ax² + By² + Cz² + 2Fxy + 2Gyz + 2Hzx + 2Px + 2Qy + 2Rz + D = 0,

где A, B, C, ..., D - действительные числа.

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты - это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

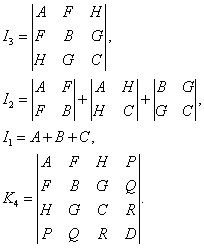
Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

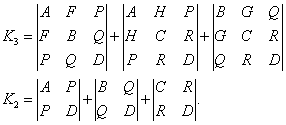
В случае, если I3 = 0, K4 = 0, семиинвариант K3 будет также и инвариантом переноса; в случае же I3 = 0, K4 = 0, I2 = 0, K3 = 0 семиинвариант K2 = 0 будет также и инвариантом переноса.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: