
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Четыре постулата термодинамикиСтр 1 из 7Следующая ⇒
Основная задача термодинамики и сущность её метода изложены в 1.5. Будем считать, что факт существования четырех постулатов или начал вам известен. Так получилось исторически, что началам термодинамики присвоены номера, начиная с нулевого. Перед тем как приступить к подробному изучению содержания постулатов постараемся сформировать представление о предназначении каждого из них как компонента целостной системы принципов. Для этого обратимся к схеме 8.1.1. Схема 8.1.1
8.2. Нулевое (общее) начало термодинамики До тридцатых годов ХХ века начал термодинамики было три. В 1931 году, когда приступили к исследованию неравновесных систем, потребовалось более строгое определение температуры. Развернулась широкая дискуссия об основах термодинамики, в результате которой было достигнуто понимание, что стремление к равновесию замкнутой системы само по себе является основополагающим принципом термодинамики. Таким образом, было сформулировано четвёртое начало. Поскольку фактически пользоваться им стали гораздо раньше, чем возникла даже классическая механика, то английский физик-теоретик Р.Г. Фаулер предложил присвоить ему номер меньший, чем первый – нулевой. Таким образом, закончилась почти столетняя история открытия законов термодинамики:
Второе начало (С. Карно, У. Томсон, Р. Клаузиус) – 1824 г. Первое (Ю.Р. Майер, Дж. Джоуль, Г. Гельмгольц) – 1842 г. Третье (В. Нернст) – 1906 г. Нулевое (по общему соглашению) – 1931 г.
Формулировка постулата Если макроскопические системы привести в непосредственный контакт и изолировать от внешней среды, то они по истечении времени придут к термодинамическому равновесию. Это равновесие не нарушится, если устранить контакт между системами, а затем через некоторое время восстановить его.
Свойство транзитивности термодинамического равновесия
Термодинамическое равновесие обладает свойством транзитивности: если системы
Информационное содержание постулата • Достигнув состояния термодинамического равновесия, изолированная система никогда самопроизвольно выйти из него не может. • Существует некоторый макроскопический параметр, значения которого при тепловом контакте различных тел в результате обмена энергии становятся для них одинаковыми. Эта величина, выражающая состояние внутреннего движения равновесной системы, называется температурой. • Свойство транзитивности состояний теплового равновесия позволяет сравнивать значения температуры у разных систем, не приводя их в непосредственный контакт между собой, а пользуясь каким-то другим телом. • Из положения о существовании температуры следует, что все равновесные внутренние параметры системы являются функциями внешних параметров и температуры.
Фундаментальное и прикладное значение постулата Общее начало является основой всей термодинамики и определяет границы ее применимости. Термодинамика не применима к системам с малым числом частиц, в которых существенны флуктуации, а также к системам галактических размеров, где важное значение имеет гравитация. Для таких объектов нулевое начало не выполняется. Нулевое начало обеспечивает полноту системы постулатов макроскопической теории. Оно является надёжным обоснованием процедуры измерения температуры с помощью термометра.
8.3. Макроскопические процессы
В термодинамически равновесном состоянии ни один параметр системы с течением времени не меняется. Внутри такой системы нет никаких макроскопических движений. Если некоторые параметры изменяются во времени, это значит, что в системе идет процесс. Термодинамический процесс – это переход из одного равновесного термодинамического состояния в другое. Процесс перехода системы из неравновесного состояния в равновесное называется релаксацией, а промежуток времени, за который он происходит, называется временем релаксации. Процесс называется равновесным или квазистатическим, если все параметры системы изменяются физически бесконечно медленно, при этом промежуточные состояния являются равновесными. Графическое изображение функциональной зависимости любых двух параметров, меняющихся в равновесном процессе, представляют в виде непрерывной линии на диаграммах – Квазистатические процессы, строго говоря, не существуют в природе. Они являются идеализацией реальных процессов, но к ним можно подойти сколь угодно близко. Многие реальные процессы, например, процессы расширения газов в цилиндрах тепловых машин можно считать приближенно квазистатическими. Заметим, что не всякий медленный процесс является равновесным, например процесс теплопроводности. Процесс, начало и конец которого совпадают, называется циклическим или просто циклом. Циклические процессы могут быть равновесными и неравновесными. Равновесный цикл на диаграмме процессов изображается замкнутой линией. Теперь уместно дать определения обратимых и необратимых процессов. обратимый процесс – это процесс, для которого существует хотя бы один способ вернуть систему из конечного состояния в начальное без каких-либо изменений в окружающих внешних телах. Необратимый процесс – это процесс, для которого невозможен обратный переход из конечного состояния в начальное без изменений в окружающих внешних телах. Например, процессы, происходящие в изолированной системе необратимы. Вернуть систему в исходное состояние можно только, если нарушить её изоляцию. Обратимые процессы подразделяют на два вида: обратимые в широком смысле слова и обратимые в узком смысле слова. Процесс, для которого возможен обратный переход из конечного состояния в начальное через те же промежуточные состояния, что и в прямом процессе называют обратимым в узком смысле слова. Если систему из конечного состояния можно вернуть в исходное состояние любым способом, то прямой процесс называют обратимым в широком смысле. Очевидно, что процесс обратимый в узком смысле слова является обратимым и в широком смысле. Всякий квазистатический процесс является обратимым и при том в узком смысле. Верно также и обратное: всякий обратимый в узком смысле процесс является равновесным. Последние два утверждения постоянно используются в термодинамике. В частности, можно сделать заключение, что всякий квазистатический циклический процесс может происходить как в прямом, так и в обратном направлении.
8.4. Функция состояния Состояние системы, как вам уже известно, определяется совокупностью независимых макроскопических параметров. Термодинамическими параметрами или термодинамическими величинами называются только те параметры, которые характеризуют систему в ее термодинамическом равновесии. Универсальным отличительным признаком термодинамических величин является их статус быть функциями состояния или не являться таковыми. Величины, не зависящие от предыстории системы и полностью определяемые её состоянием в данный момент, т.е. совокупностью не зависимых параметров, называются функциями состояния. Естественно, что каждый из независимых параметров является сам функцией состояния системы. Например, температура Определение статуса величин, зависящих от двух параметров, требует проведения специального анализа или диагностики, исходя из физических признаков и математических свойств этих величин. Физические признаки мы сформулируем на основе приведенного выше определения функции состояния и представления о термодинамических процессах. Итак, функция состояния обладает следующими признаками: онаоднозначно определяет состояние системы, т.е. её значение не зависит от вида процесса, с помощью которого система приведена в данное состояние, поэтому её изменение в циклическом процессе равно нулю.
Математические свойства функции состояния
Бесконечно малое приращение функции состояния
Полный дифференциал можно представить в форме
где
Кроме того, должно выполняться равенство
Оно является необходимым и достаточным условием утверждения (8.1). Далее мы рассмотрим важнейшие исходные термодинамические величины, дадим им микроскопическую и макроскопическую трактовку, а также определим их статус.
8.5. Внутренняя энергия системы. Работа и теплота Внутренняя энергия
Микроскопическая трактовка внутренней энергии системы была нами дана в первой части лекционного курса (см. 7.1-7.2) на примере идеальных систем. Обобщим эти представления на реальные системы. Внутренняя энергия системы равна сумме кинетической энергии движения молекул и составляющих их частей и потенциальной энергии взаимодействия между молекулами и атомами внутри молекул. К внутренней энергии не относятся потенциальная энергия молекул во внешнем силовом поле и кинетическая энергия центра масс системы. В термодинамической (макроскопической) трактовке внутренняя энергия Для идеальной системы (системы без межмолекулярного взаимодействия) Внутренняя энергия обладает всеми признаками и математическими свойствами, определенными в 8.4., поэтому внутренняя энергия есть функция состояния системы.
Макроскопическая работа и теплота
При взаимодействии термодинамической системы с окружающей средой происходит обмен энергией. Возможны два способа передачи энергии от системы к внешним телам и от внешних тел к системе. Первый способ связан с совершением работы, а второй с теплообменом. При совершении работы изменяются внешние параметры системы. Работа как процесс представляет собой макроскопическую передачу энергии в упорядоченной форме путем взаимного действия системы и внешних тел друг на друга. Работа как результат – это энергия, переданная системой указанным способом. При теплообмене (без совершения работы) внешние параметры остаются неизменными. Энергия, переданная системе в результате теплообмена от окружающих тел, называется количеством теплоты, полученным системой в таком процессе. Работа
 Определим работу, которую совершает газ, находящийся в цилиндрическом сосуде с поршнем (рис. 8.1), в результате его квазистатического расширения с изменением объема от Определим работу, которую совершает газ, находящийся в цилиндрическом сосуде с поршнем (рис. 8.1), в результате его квазистатического расширения с изменением объема от 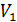 до до 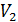 . В данном случае . В данном случае 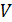 – это единственный изменяющийся внешний параметр системы. – это единственный изменяющийся внешний параметр системы.
Для вычисления работы надо прежде всего найти силу, действующую на поршень. Газ действует на поршень, площадь сечения которого Бесконечно малая или элементарная работа, совершаемая газом при перемещении поршня на Положительной считается работа, совершаемая газом против внешних сил при его расширении:
На диаграмме процесс.
С молекулярно-кинетической точки зрения количество теплоты – это мера обмена энергией между хаотически движущимися молекулами взаимодействующих макроскопических тел. В заключение еще раз подчеркнем, что можно говорить о приращении внутренней энергии, но нельзя говорить о приращении работы или теплоты. Можно говорить только о количестве теплоты, полученном системой, и совершенной ею работе в том или ином процессе.
8.6. Калорическое и термическое уравнения состояния Эти термины используются в термодинамике для именования хорошо известных вам уравнений. Калорическое уравнение состояния или уравнение энергии – это, конечно, В дальнейшем мы убедимся, что термическое и калорическое уравнения состояния не являются независимыми. Они связаны дифференциальными уравнениями в частных производных. Вывести уравнения состояния на основе начал термодинамики нельзя. Они или находятся из опыта или выводятся методами статистической физики. Для идеального газа термическим уравнением состояния является уравнение Клапейрона-Менделеева, Из термического уравнения состояния можно вывести три термических коэффициента. Термические коэффициенты – это величины характеризующие изменение какого-либо параметра Термические коэффициенты описывают важные в практическом отношении свойства различных веществ. Из (8.6) следует, что если известны два любых термических коэффициента, то можно вычислить третий. Это особенно актуально для нахождения
Схема 8.6.1.
Подобно трём термическим коэффициентам употребляются также три термодинамических коэффициента (см. схему 8.6.2).
Схема 8.6.2.
Следует отметить, что в учебной литературе по термодинамике многие авторы не делают строгого разграничения между термическими и термодинамическими коэффициентами, за исключением И.П. Базарова [1]. Зачастую коэффициенты обеих групп называют термическими или даже тепловыми. Контрольные вопросы 1. Какова функциональная роль каждого из четырех начал термодинамики? 2. Сформулируйте нулевое начало. Какова область его применимости? 3. Каким образом вводится температура в термодинамике? 4. Как следует понимать свойство транзитивности термодинамического равновесия? В чем состоит его практическое значение? 5. Какой процесс называется: а) термодинамическим; б)квазистатическим; в) релаксацией; г) обратимым в узком смысле слова; д) обратимым в широком смысле слова? 6. Каким образом можно установить является данная термодинамическая величина функцией состояния или нет? 7. Дайте микроскопическую и макроскопическую трактовку внутренней энергии системы. 8. Определите следующие понятия: работа как процесс и работа как результат. 9. Что называется количеством теплоты? Дайте микроскопическую трактовку этому понятию. 10. Какие из перечисленных ниже величин являются функциями состояния: 11. Запишите формулу для вычисления работы, совершенной газом, в результате его квазистатического расширения. Поясните ее смысл с помощью графика процесса. 12. Что характеризуют термические коэффициенты? Запишите формулы для термических коэффициентов расширения, сжатия и давления, а также соотношение связывающее их между собой.
ЛЕКЦИЯ 9
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
9.1. Первое начало термодинамики
Первое начало термодинамики было установлено как результат обобщения экспериментальных и теоретических исследований в области физики и химии, завершающим этапом которых явилось открытие эквивалентности теплоты и работы. Многие учёные претендовали на авторство этого закона. Приоритет разделила тройка лидеров: Роберт Майер, Джеймс Джоуль и Герман Гельмгольц.
Формулировка постулата
Количество теплоты, сообщенное макросистеме, идет на приращение ее внутренней энергии и на совершение системой работы против внешних сил. Математическая запись постулата
Дифференциальная форма уравнения первого начала имеет вид
где Уравнение первого начала может быть представлено в интегральной форме
Информационное содержание постулата
• Внутренняя энергия системы является функцией состояния, которая изменяется только под воздействием окружающей среды. Это отражено в дифференциальной форме записи уравнения постулата. • Закон сохранения энергии не определяет направление развития процесса, а только согласовывает взаимное изменение таких величин как • Уравнение первого начала применимо как к равновесным, так и к неравновесным процессам. Оно не запрещает полностью преобразовать количество теплоты, полученное системой, в макроскопическую работу. • Первое начало запрещает существование вечного двигателя первого рода, т.е. машины, совершающей работу без затрат энергии и без поступления количества теплоты извне.
Фундаментальное и прикладное значение постулата Первое начало дает математическое выражение количественной стороны закона сохранения и превращения энергии в термодинамических системах, позволяет решать множество прикладных задач, например, таких как: • Определение теплоёмкостей макросистем в различных процессах и установление связей между ними. • Вывод уравнений различных процессов. • Вычисление показателей эффективности тепловых машин. • Расчёт теплового эффекта химических реакций.
Далее мы рассмотрим большинство из перечисленных следствий и приложений первого начала.
9.2. Теплоёмкость Микроскопическую природу этого физического свойства макросистем мы с вами уже обсуждали и даже научились вычислять теплоёмкости многоатомных газов и твердых тел путем подсчёта числа статистических степеней свободы. Далее мы продолжим обсуждение предмета в рамках феноменологического, то есть термодинамического подхода. Напомним определение теплоёмкости: Теплоемкостью называется количество теплоты, которое нужно сообщить системе, чтобы изменить ее температуру на 1 К. Главный вывод из ранее изученного материала заключается в том, что теплоёмкость зависит как от свойств макросистемы, так и от самого процесса передачи энергии. Теплоёмкости при постоянном объёме и при постоянном давлении играют важную роль, поскольку без их знания невозможно проведение полного термодинамического анализа системы. На схеме 9.2.1 приведены термодинамические определения Как видно из схемы наш список функций состояния пополнился тремя величинами. Это энтальпия Схема 9.2.1.
Связь между теплоёмкостями
Описание системы Рассматриваемая термодинамическая система является закрытой, т. е. она может обмениваться энергией с окружающей средой.
Актуальная информация о процессе и системе
• Процесс теплообмена является квазистатическим. • Известно термическое уравнение состояния данной системы • Известно калорическое уравнение состояния
Постановка задачи Найти соотношение между молярными теплоёмкостями Вывод формулы
• Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
• Представим полный дифференциал внутренней энергии через частные производные по параметрам
После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость • Рассмотрим процесс при постоянном давлении
Исходя из полученной формулы, можно легко найти связь между теплоемкостями
Уравнение Роберта Майера Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда
Окончательно запишем
Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости Вывод уравнения политропического процесса в идеальном газе • Требование постоянства теплоёмкости
• Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
• Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
• Разделив (
• Интегрированием (9.15), получаем
где
Это уравнение политропы в переменных Исключая из уравнения (
где
Параметр К этому классу процессов относится также адиабатный или адиабатический процесс. Адиабатным называется процесс, проходящий без теплообмена ( Из определения теплоемкости следует, что в адиабатическом процессе
где В этом случае уравнение политропы принимает вид
Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр Популярное:
|
Последнее изменение этой страницы: 2016-03-17; Просмотров: 1124; Нарушение авторского права страницы