Определение положения точки в пространстве. Вектор перемещения.

Определение положения точки в пространстве. Вектор перемещения.

Для описания движения точки, т.е. изменения ее положения с течением времени, прежде всего, надо в любой момент времени указать ее местоположение координатным или векторным способом. Оба способа задания положения тела в пространстве эквивалентны, т.е. зная координаты точки, можно указать ее радиус-вектор, и наоборот. Из рис. 1 видно, что радиус-вектор представить можно

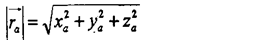диагональю прямоугольного параллелепипеда со сторонами, численно равными координатам точки Х_а, Y_a и Z_a. Отсюда очевидна связь модуля радиус-вектора точки с ее координатами:

Для определения направления радиус-вектора в пространстве можно определить углы a, b, g, которые радиус-вектор образует с координатными осями OX, OY, и OZ соответственно. Тогда:

Таким образом, зная координаты точки, можно определить величину (1) радиус-вектора, и его направление в пространстве по так называемым направляющим косинусам (2), (3) и (4).

При движении точки ее координаты и радиус-вектор с течением времени изменяются, для определения характеристик движения вводят три вектора: перемещения, скорости и ускорения.

ВЕКТОР ПЕРЕМЕЩЕНИЯ.

Рис. 2

Для определения перемещения точки в пространстве вводят вектор перемещения.

Например, за промежуток времени Dt точка перемещается из положения 1 в положение 2 (рис. 2), определяемые векторным способом указанием радиус-векторов и; вектором перемещения называют вектор, проведенный из начального положения 1 в конечное 2 перемещаемого тела. Из векторного треугольника видно, что вектор перемещения равен приращению радиус-вектора точки.

Наряду с изменением радиус-вектора точки происходит изменение ее координат, т.е. перемещение точки вдоль отдельных координатных направлений. Из рис.3 видно, что

Вектор перемещения за конечный промежуток времени в общем случае не совпадает с направлением движения (направлением касательной к траектории движения). Очевидно, что эти направления будут совпадать в общем случае движения только для бесконечно малых перемещений точки.

Вектор скорости. Вектор ускорения. Тангенциальное и нормальное ускорение

Вектором скорости называют вектор, определяющий быстроту и направление движения.

Вектором средней скорости называют отношение вектора перемещения к промежутку времени, за который это перемещение происходит:

Так как в произвольном случае движения вектор перемещения за конечный промежуток времени не определяет точно направление движения, это не может сделать и вектор средней скорости. Следовательно, необходимо рассматривать перемещения за бесконечно малые промежутки времени.

Вектором истинной (мгновенной) скорости называют предел, к которому стремится значение вектора средней скорости при бесконечном убывании промежутка времени:

Так как при движении тела в общем случае изменяются все три его координаты, часто бывает удобным рассматривать скорость движения точки вдоль отдельных координатных направлений (компоненты или составляющие вектора скорости). Компоненты средней скорости равны:

Компоненты же мгновенной скорости определяются как

Вектор скорости с его компонентами связан такими же по виду соотношениями, как радиус-вектор с

координатами точек:

Вектор Ускорения

Вектором ускорения называют вектор, определяющий быстроту и направление изменения вектора

скорости. Аналогично определениям для вектора скорости вводятся понятия среднего и мгновенного

ускорения:

При движении точки по произвольной траектории вектор изменения скорости Δ J и, следовательно, вектор ускорения направлены в сторону вогнутости траектории независимо от того, увеличивается или уменьшается величина скорости.

Статическое и динамическое проявление сил. Законы Ньютона. Принцип независимости действия сил.

Момент силы относительно произвольного центра. Момент силы относительно произвольной оси.

Основной закон динамики.

Постулаты Эйнштейна.

В основе специальной теории относительности, прежде всего, лежит факт постоянства скорости света в различных системах отсчета, что противоречит классическому закону сложения скоростей. Кроме того, нет никаких оснований считать, что механические опьггы позволят отличить одну инициальную систему отсчета от другой. Это позволило Эйнштейну сформулировать исходные постулаты специальной теории относительности.

Постулат о постоянстве скорости света: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источника и приемника света.

Постулат относительности (общефизический принцип относительности): Никакими физическими опытами нельзя отличить одну инерциальную систему отсчета от другой. Наряду с этими постулатами Эйнштейн ввел принцип синхронизации часов, имеющий такое же значение в теории относительности, как и сформулированные выше постулаты.

Для того, чтобы одинаковые по устройству часы А и В (рис.31)

шли одинаково, необходимо их синхронизировать. Пусть в момент времени, отсчитанный по часам А, в том месте, где они находятся, осуществляется световая вспышка. Сигнал от нее достигает часов В, мгновенно отражается и поступает к часам А в момент времени, отсчитанный по ним. Часы А и В считаются синхронизированными, если в момент отражения сигнала в т. В показания часов равны:

По сути дела в принципе синхронизации постулируется утверждение, что прямой и отраженный сигналы движутся с одинаковой скоростью, а само отражение происходит мгновенно, что не следует из сформулированных ранее постулатов.

Исходя из указанных постулатов, можно получить все основные выводы специальной теории относительности.

" Радиолокационный" метод (метод коэффициента " k " ).

Движение тел можно графически представлять диаграммами x=x(t). В случае скоростей, сравнимых со скоростью света, масштаб х и t выбирается таким, что траектория светового сигнала (" световая линия" ) делит координатный угол пополам. Если же тело движется со скоростью, меньшей скорости света, угол наклона его траектории к оси t меньше 45°.

Предположим, что две инерциальные системы отсчета А и В находятся в относительном движении. Систему А условно считаем неподвижной. В исходный момент времени системы полностью совпадали. В этот момент осуществляется синхронизация подвижных и неподвижных часов и на них устанавливаются нулевые показания. Далее система В удаляется от А со скоростью v< c (рис.32).

Затем в системе А производится вторая вспышка в момент времени t, измеренный по часам А. Сигнал от нее догоняет систему В в момент времени, измеренный по часам В в подвижной системе, а показания неподвижных часов А для этого события равны. Сигнал мгновенно отражается и приходит в систему А в момент времени, отсчитанный по часам А.

Предположим, что показания подвижных часов в момент отражения сигнала в k раз отличаются от показаний неподвижных часов t в момент посылки сигнала: = kt (148)

Системы равноправны, поэтому с момента отражения неподвижной можно считать систему В, а систему А - подвижной. Тогда показания часов А в момент приема сигнала равны:

С момента синхронизации до отражения сигнала система В и световой сигнал, посланный в момент времени t (по часам А), проходят одинаковый путь:

откуда получаем значение коэффициента k:

Следовательно, показания подвижных часов в момент приема сигнала всегда больше показаний неподвижных часов в момент посылки сигнала:

18. Замедление" хода времени. Относительная скорость.

Замедление хода времени

Рассмотрим на описанном выше примере промежуток времени между двумя событиями (синхронизация часов и отражение сигнала), измеренный по часам А и В. Поскольку в момент синхронизации показания обоих часов нулевые, то промежуток времени численно равен показаниям часов в момент отражения сигнала. Обозначив промежуток времени, измеренный по часам А и В, соответственно и , отношение этих показаний запишем в виде:

Откуда:

Следовательно, промежуток времени между двумя событиями, измеренный подвижными часами, меньше результата того же измерения по неподвижным часам.

Относительная скорость.

Предположим, что системы А, В и D находятся в относительном движении. В исходный момент все три системы совпадали. В этот момент производим синхронизацию всех часов и устанавливаем на них удаляется от А со скоростью v₁, а система D - со скоростью v₂ > v₁. В момент времени t (пo часам А) в системе А производится световая вспышка, сигнал от которой достигает (рис.33)нулевые показания. Далее система В удаляется от А со скоростью v₁, а система D - со скоростью v₂ > v₁. В момент времени t (пo часам А) в системе А производится световая вспышка, сигнал от которой достигает (рис.33)

системы В в момент t_B =k₁t (по часам В) и системы D в момент t_D =k₂t (по часам D). При этом:

Теперь будем считать систему В неподвижной, а систему D - удаляющейся от B с относительной скоростью и. Тогда:

Следовательно:

Откуда:

Это и есть выражение для относительной скорости.

19. Сравнение поперечных размеров тел. Эффект " сокращения" длин.

Пусть две системы OXYZ и O'X'Y'Z' находятся в относительном движении. Одну из них, OXYZ, считаем неподвижной, другая же движется со скоростью v относительно первой так, что оси ОХ, 0'Х' и 0Z, О’Z' остаются параллельными, а ось О’Y' скользит вдоль оси OY. В подвижной системе вдоль оси O'Z' расположены " световые часы" (жесткий стержень с двумя зеркалами на концах, отражающими поверхностями друг к другу) так, что нижнее зеркало совпадает с началом системы отсчета (рис.34). В исходный момент, когда системы полностью совпадали, у нижнего зеркала произошла световая вспышка. Сигнал от нее достигает верхнего зеркала, отражается, приходит опять к нижнему зеркалу, и далее процесс повторяется периодически. Пусть по неподвижным часам промежуток

времени между вспышкой и приходом сигнала равен t. За это время в неподвижной системе световой сигнал проходит путь сt, а подвижная система - vt. Из рисунка видно, что длина световых часов, численно равная координате z верхнего зеркала, в неподвижной системе равна:

В подвижной системе, связанной с подвижными часами, длина их равна:

z'=ct' (158)

где: t' - полупериод часов, т.е. промежуток времени между вспышкой и приходом сигнала к верхнему зеркалу.

Учитывая эффект " замедления" хода времени, получаем:

т.е. поперечные размеры (по отношению к направлению движения) тел одинаковы в обеих системах отсчета:

z'=z

Эффект " сокращения" длин.

Пусть теперь световые часы ориентированы вдоль оси подвижной системы так, что левое зеркало совпадает с ее началом. В исходный момент системы совпадали, и в этот момент у левого зеркала произошла вспышка. Сигнал от нее достигает правого зеркала через промежуток

времени t₁ по неподвижным часам (рис.35). Тогда:

где: l - длина световых часов, измеренная в неподвижной системе.

После отражения сигнал и левое зеркало движутся навстречу друг другу и встречаются в момент времени t₂ по неподвижным часам. Очевидно, что:

Период световых часов, измеренный в неподвижной системе, равен:

В подвижной системе период часов определяется соотношением:

где l' - длина часов, измеренная в подвижной системе. Отсюда:

т.е.:

Следовательно, продольные размеры тел в любой системе меньше собственных:

20. Преобразования Лоренца. Интервал. Инвариантность интервала.

Преобразования Лоренца дают связь между пространственными и временными координатами событий в двух инициальных системах отсчета, находящихся в относительном движении.

Учитывая, что поперечные размеры тел одинаковы, получаем:

z'=z (166)

х'=x (167)

Для сравнения координат у обратимся к предыдущему примеру:

С другой стороны, это соотношение можно представить в виде:

Соотношения (166, 167, 168, 170) называют преобразованиями Лоренца.

Интервал. Инвариантность интервала.

Интервалом S между двумя событиями называют величину, квадрат которой равен:

где x_i, y_i, z_i, t_i - пространственные и временные координаты событий.

Используя преобразования Лоренца, запишем интервал в подвижной системе отсчета:

Таким образом, интервал является инвариантом:

S ^/2=S ² (171)

В зависимости от соотношения между временной cΔ t и -

пространственной частями интервала различают:

1.Времениподобные интервалы (cΔ t > Δ l).

2.Пространственноподобные интервалы (cΔ t < s Δ l).

3. Светоподобные интервалы (сΔ t = Δ l).

Вязкое трение

Вязкое трение возникает при относительном движении слоёв жидкости или газа. Основные законы вязкого трения получены опытным путём.

Ньютон установил, что если под действием силы площадка площади движется равномерно

со скоростью относительно площадки (рис.45),

На подвижную площадку действуют силы сопротивления движению (силы вязкого трения):

(191)

где - расстояние между площадками (слоями), - коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.

При движении тел в вязкой среде на них действуют силы сопротивления движению.

Стокс получил выражение для этих сил. При малых скоростях.

(192)

где: - стоксова сила сопративления, - плотность среды, - скорость тела, -коэффициент, определяемый геометрией тела, - площадь проекции тела на плоскость, перпендикулярную направлению движения.

Движение тел в сопротивляющейся среде.

При достаточно больших скоростях тел (или если форма тела является плохо обтекаемой) силы Стокса становятся пропорциональны квадрату скорости: (193)

Положим, что тело начинает падать под действием силы тяжести в сопротивляющейся среде. Пренебрегая силой Архимеда, запишем:

(194)

С течением времени скорость тела возрастает, возрастает и сила Стокса. Наконец, силы тяжести и Стокса уравновешиваются, после чего начинается равномерное движение тела с установившейся скоростью . Определим зависимость скорости от проходимого телом пути и значение установившейся скорости. Для этого сначала преобразуем (194):

Обозначим:

Тогда:

Или:

(195)

Интегрируя (195), получим:

(196)

Константу интегрирования находим из начальных условий (x=0 и =0):

(197)

Подставив (197) в (196) получим

Или:

Откуда:

(198)

Через достаточно большой промежуток времени ( ) скорость тела перестаёт изменяться. Следовательно, значение установившейся скорости равно

(199)

(178) и (179) и дают искомое решение поставленной задачи.

Деформация кручения.

Деформации кручения возникают при закручивании одного основания образца относительно другого:

По закону Гука для этого типа деформации: (210)

где - угол закручивания, - длина образца, - момент закручивающих сил, - коэффициент кручения.

Величина называется модулем кручения т. е. (211) Одновременно с закручиванием образца происходит сдвиг его слоёв. Угол сдвига определяется из закона Гука.

(212)

Угол сдвига можно получить и из чисто геометрических соображений: (213)

Сравнивая (212) и (213), получим Момент распределённых сил, приложенных к нижнему основанию образца, получим, используя

Из рис.51 видно, что элементарный момент закручивающих сил, приложенных к элементу основания, равен:

(215)

Полный момент: (216)

Сравнивая (210) и (216), получаем связь между модулями сдвига и кручения: (217)

Закон всемирного тяготения.

Закон всемирного тяготения получен Ньютоном из наблюдений видимого движения планет Солнечной системы, используя законы динамики. В векторной форме закон всемирного тяготения, определяющий силы гравитационного взаимодействия, имеет вид: (218)

где - масса источника гравитационного поля, - величина пробной массы, -радиус-вектор точечной пробной массы относительно центра масс источника поля, - гравитационная постоянная.

Силовой характер поля источника является сила, действующая на единичную пробную массу, помещённую в данную точку поля. Эта величина называется напряжённостью поля: (219)

Следует отметить, что закон всемирного тяготения справедлив только для точечных взаимодействующих масс. Кроме того, массы тел, фигурирующие в законе всемирного тяготения, имею другой смысл, нежели в законах динамики. Это –“тяготеющие”, ”тяжёлые” или ”гравитационные” массы.

Работа упругих сил.

На гладкой горизонтальной плоскости находится тело, скрепленное пружиной жесткости с вертикальной стенкой (рис.55).

Если под действие внешней силы пружина растягивается на , возникает сила упругости пружины, равная в пределах упругих деформаций . Элементарная работа упругих сил по перемещению тела из этого положения на равна:

Работа же силы на конечном перемещении: (238)

где – растяжение (удлинение) пружины.

Потенциальная энергия.

Потенциальной энергией называют энергию, определяемую конфигурацией системы, относительным расположением отдельных взаимодействующих тел. выражение для потенциальной энергии для произвольного взаимодействия записать сложно, обычно определяют ее изменение относительно уровня, условно принятого за нулевой. например, потенциальная энергия тела массы m в поле тяготения Земли, находящегося на высоте h над ее поверхностью:

а на поверхности:

Изменение потенциальной энергии тела относительно поверхности Земли:

При « (225) принимает вид:

Таким выражением и пользуются, как правило, при расчетах. Здесь потенциальная энергия отсчитывается от определенного уровня (поверхности Земли), на которое она условно принята нулевой.

Такой подход оправдан тем, что при изменениях конфигурации систем изменение состояния определяется не самим значением потенциальной энергии, а только изменением ее.

Теорема Штейнера.

Расчет моментов инерции тела даже правильной формы, если ось не проходит через центр масс тела, затруднен. В этом случае удобно пользоваться теоремой Штейнера:

Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси , параллельной заданной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями:

Для доказательства через центр масс тела (т. С) проведем ось , параллельную заданной оси (рис. 61). Расстояние между осями равно . Выберем частицу тела массы , настояние от нее до осей и указаны на рисунке.

Момент инерции тела относительно по определению: (262)

Из геометрических соображений:

Первое слагаемое в правой части дает момент инерции тела относительно :

(263)

Поскольку a=const, второе слагаемое принимает вид (Ma²), где М - масса тела.

В последнем слагаемом:

следовательно, по определению центра масс:

последнее слагаемое обращается в нуль, поэтому:

что и требовалось доказать.

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ

(264)

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ

(265)

ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА

В любой момент времени плоское движение можно представить, как вращение вокруг мгновенного центра вращения, пусть О -мгновенный центр вращения, а т. С - центр с масс тела. Тогда:

(266)

где: и - моменты инерции тела относительно осей, проходящих через центр масс и мгновенный центр вращения, - расстояние между осями, . - скорость центра масс поступательной части движения), (омега) - угловая скорость вращения вокруг оси, проходящей через центр масс.

2. Вращательное движение

Прецессия волчка.

Быстро вращающийся симметричный волчок установлен на горизонтальную поверхность (рис. 67). Точка касания неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр .

при указанном направлении вращения момент силы тяжести вызывает прецессию в направлении, указанном на рисунке. Угловую скорость прецессии

можно определить, пользуясь (274):

т.е (275)

Следовательно, угловая скорость прецессии тем меньше, чем больше угловая скорость собственного вращения.

ЗАКОН ПАСКАЛЯ.

Жидкость покоится в поле тяготения Земли. В этом случае уравнения Эйлера имеют вид:

С учетом (282) и (283) последнее уравнение (284) принимает вид:

откуда: (286)

где удельный вес жидкости. Интегрируя (286), получаем (287)

Постоянная интегрирования будет определена, если в точке с координатой z₀ известно давление p₀ . Тогда

Последнее выражение обычно записывают в виде:

(288)

т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/g)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.

Закон Архимеда.

Тело погружено в жидкость

На его поверхность со стороны жидкости действуют силы давления, выделим в теле объем малого сечения, ось которого вертикальна. На верхнюю и нижнюю грани этого объема действуют силы давления

Равнодействующая сил давления в проекции на вертикальную ось равна:

где: dS - проекция dS₁ (или dS₂) на горизонтальную плоскость. Разность давлений по закону Паскаля равна

где: dZ - разность уровней центров граней выделенного объема. Тогда равнодействующая сил давления равна

где dV - величина выделенного объема.

Вертикальная проекция сил давления, действующих на всю смоченную поверхность тела, может быть получена путем интегрирования предыдущего выражения:

т.е. сила, действующая со стороны жидкости на погруженное в нее тело по величине равна весу жидкости, вытесненной телом.

Формулировка закона: на тело, погруженное в жидкость действует выталкивающая сила, равная весу жидкости в объеме, вытесненном телом, и приложенная в той точке смоченной поверхности тела, в которой вертикаль, проведенная через центр масс вытесненной жидкости, пересекает эту поверхность.

Существенным в формулировке закона Архимеда является правильное указание точки приложения выталкивающей силы. Действительно, поскольку сила Архимеда обусловлена действием распределенных по поверхности сил давления со стороны жидкости, то и равнодействующая сил давления должна быть приложена к смоченной поверхности тела (но не к центру масс вытесненной жидкости, как это часто утверждается). Кроме того, наличие в плавающем теле деформаций можно объяснить только при таком рассмотрении силы Архимеда.

ОПРЕДЕЛЕНИЯ

1.Линией тока называют кривую, в каждой точке которой касательные к ней совпадают по направлению с вектором скорости в данный момент времени.

2.Поверхностью тока называют поверхность, образованную линиями в тока.

3.Поверхность тока, проходящую через замкнутый контур, называют трубкой тока.

4.Часть потока жидкости, ограниченную трубкой тока, называют струёй жидкости.

Пpи установившемся потоке жидкость внутри трубки тока а движется как в трубке с твердыми стенками.

ФОРМУЛА ТОРИЧЕЛЛИ

формула Торричелли позволяет определить скорость истечения жидкости из отверстия в сосуде. Предположим, что в широкий сосуд площади сечения S налита жидкость, свободная поверхность которой находится на высоте Z над центром малого отверстия площади в боковой стенке сосуда (рис.76). Давление на свободной поверхности жидкости н в вытекающей струе непосредственно за отверстием равно атмосферному Р_а. Пусть скорость истечения жидкости равна , а скорость понижения уровня жидкости в сосуде - . Жидкость будем считать несжимаемой.

Запишем уравнение Бернулли, сравнивая сечение для свободной поверхности жидкости с сечением отверстия:

Т.к. площадь сечения отверстия мала по сравнению с сечением сосуда, а жидкость несжимаема, то:

откуда следует формула Торричелли:

Собственные колебания.

Предыдущая12 3 4 5 6 7 8 9 10 Следующая