Интерполяционная формула Лагранжа.
 Интерполяционная формула Лагранжа есть формула полинома степени
Интерполяционная формула Лагранжа есть формула полинома степени 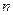 , проходящего через все узлы интерполяции. То есть, через
, проходящего через все узлы интерполяции. То есть, через 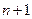 точки можно провести единственный полином степени n
точки можно провести единственный полином степени n
Построим такой полином.
Введём полином
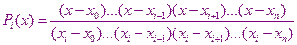
Легко убедится, что во всех точках 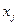 кроме точки
кроме точки 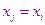 .
.
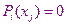 , если
, если 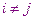
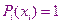 , если
, если 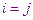

Отсюда следует, что искомый полином, проходящий через все табличные точки можно представить в виде
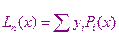
Так как 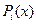 - это полином степени
- это полином степени 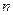 , то и
, то и 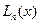 тоже является полиномом степени
тоже является полиномом степени 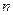 .
.
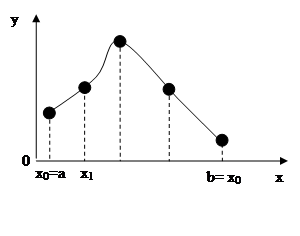
Другого полинома отличного от полинома Лагранжа проходящего через все узлы 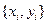 быть не может. С помощью полинома Лагранжа можно вычислить приближённое значение аппроксимируемой функции
быть не может. С помощью полинома Лагранжа можно вычислить приближённое значение аппроксимируемой функции 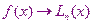 для любого
для любого 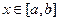 . Таким образом, нахождение аппроксимируемой функции для значений х внутри заданного отрезка
. Таким образом, нахождение аппроксимируемой функции для значений х внутри заданного отрезка 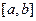 , называется интерполяцией, а за пределами экстраполяцией. Экстраполяция даёт значительно большую погрешность, чем интерполяция, поэтому её желательно избегать.
, называется интерполяцией, а за пределами экстраполяцией. Экстраполяция даёт значительно большую погрешность, чем интерполяция, поэтому её желательно избегать.
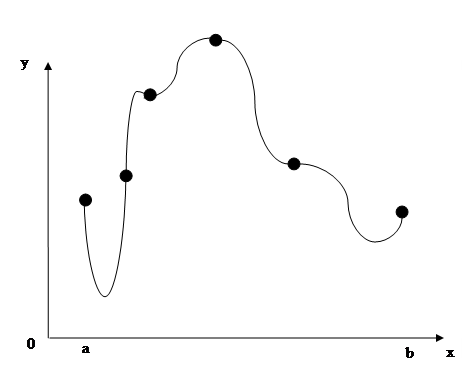 Вычисление полинома Лагранжа обычно не представляет трудности, однако пользоваться им следует с достаточной осторожностью. Дело в том, что полином Лагранжа, особенно при больших значениях может испытывать резкие колебания (особенно сильные вблизи концов отрезка интерполирования
Вычисление полинома Лагранжа обычно не представляет трудности, однако пользоваться им следует с достаточной осторожностью. Дело в том, что полином Лагранжа, особенно при больших значениях может испытывать резкие колебания (особенно сильные вблизи концов отрезка интерполирования 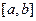 ). Поэтому при некоторых значениях аргумента полином Лагранжа может давать значительную погрешность.
). Поэтому при некоторых значениях аргумента полином Лагранжа может давать значительную погрешность.
Эта погрешность непрерывно распределена на отрезке 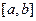 . При равноотстоящих узлах наибольшая точность наблюдается в середине интервала
. При равноотстоящих узлах наибольшая точность наблюдается в середине интервала 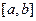 , а наименьшая вблизи концов интервала. Можно построить интерполяционный полином для которого погрешность равномерно распределена по отрезку
, а наименьшая вблизи концов интервала. Можно построить интерполяционный полином для которого погрешность равномерно распределена по отрезку 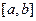 , для этого узлы должны являться корнем полинома Чебышева.
, для этого узлы должны являться корнем полинома Чебышева.
Метод 2
СПЛАЙНЫ
При большом числе узлов интерполяции { 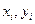 } использование полинома Лагранжа может оказаться нежелательным, в этом случае аппроксимацию можно производить с помощью сплайнов.
} использование полинома Лагранжа может оказаться нежелательным, в этом случае аппроксимацию можно производить с помощью сплайнов.
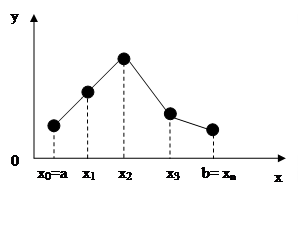
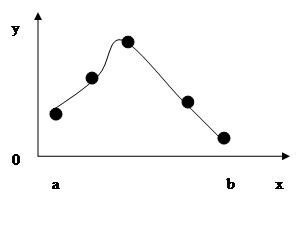
Сплайн – это функция, которая вместе с несколькими производными непрерывна на всём заданном отрезке [a, b], а на каждом частичном отрезке { 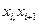 } в отдельности является полиномом некоторой степени. Максимальная по всем частичным отрезкам степень полинома называется степенью сплайна. Простейшим сплайном, сплайном 1-й степени, является кусочно-линейная функция. Представим уравнение сплайна для
} в отдельности является полиномом некоторой степени. Максимальная по всем частичным отрезкам степень полинома называется степенью сплайна. Простейшим сплайном, сплайном 1-й степени, является кусочно-линейная функция. Представим уравнение сплайна для 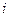 -го интервала в виде уравнения
-го интервала в виде уравнения 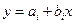 . Найдём коэффициенты сплайна
. Найдём коэффициенты сплайна 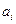 и
и 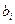 для этого используем следующие условия непрерывности.
для этого используем следующие условия непрерывности.
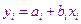
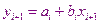
Из этих условий получаем
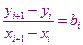
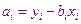
Метод 3
Сплайны третьей степени
На практике широкое распространение получили сплайны 3-ей степени, имеющие на всём [ 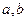 ] непрерывную первую и вторую производные. Эти сплайны называются кубическими, обычно их обозначают
] непрерывную первую и вторую производные. Эти сплайны называются кубическими, обычно их обозначают 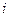
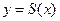 . На
. На 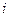 -ом частичном отрезке сплайн можно представить в виде полинома
-ом частичном отрезке сплайн можно представить в виде полинома
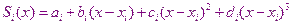
Для нахождения коэффициентов 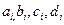 используются условия непрерывности сплайна и его 1-ой и 2-ой производных во всех узлах.
используются условия непрерывности сплайна и его 1-ой и 2-ой производных во всех узлах.
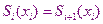 - условие непрерывности для каждого узла;
- условие непрерывности для каждого узла;
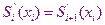 - условие непрерывности для первой производной;
- условие непрерывности для первой производной;
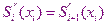 - условие непрерывности для второй производной.
- условие непрерывности для второй производной.
В результате образуется система линейных уравнений, решая которую можно найти коэффициенты сплайна 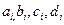
Метод 4
Метод наименьших квадратов
Полином Лагранжа и сплайны в точности проходят через экспериментальные точки ( 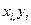 ) такой подход при аппроксимации экспериментальных данных не всегда оправдан.Дело в том, что данные (
) такой подход при аппроксимации экспериментальных данных не всегда оправдан.Дело в том, что данные ( 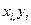 ) полученные экспериментально имеют определенную погрешность.
) полученные экспериментально имеют определенную погрешность.
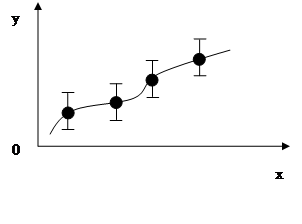
Её даже изображают графически. Графически изображают не только полученные значения, но и приделы этих значений. Поэтому аппроксимирующая зависимость не обязана в точности проходить через экспериментальные точки, а только по возможной близости к ним. Пусть 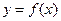 аппроксимирующая зависимость, тогда
аппроксимирующая зависимость, тогда 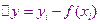 это величина, характеризующая отклонение экспериментальных данных от аппроксимирующей зависимости. Эта величина может быть как положительной, так и отрицательной, что делает её неудобной в качества меры близости данных аппроксимирующей функции. Поэтому удобней использовать квадрат этой величины.
это величина, характеризующая отклонение экспериментальных данных от аппроксимирующей зависимости. Эта величина может быть как положительной, так и отрицательной, что делает её неудобной в качества меры близости данных аппроксимирующей функции. Поэтому удобней использовать квадрат этой величины.
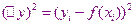
Для того, чтобы аппроксимирующая функция 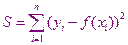 была по возможности близкой ко всем экспериментальным точкам функция
была по возможности близкой ко всем экспериментальным точкам функция 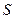 должна иметь минимальное из возможных значений. Метод нахождения аппроксимирующей функции использующей это называется методом наименьших квадратов.
должна иметь минимальное из возможных значений. Метод нахождения аппроксимирующей функции использующей это называется методом наименьших квадратов.
Обычно аппроксимирующую зависимость выбирают из некоторого класса функций зависящих от определенного числа параметров.

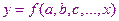
Параметры 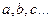 подбирают таким образом, чтобы обеспечить минимальное значение этой величины. Используя условия минимума (условие экстремума) для функции, зависящей от нескольких переменных. Мы получили систему уравнений для нахождения параметров
подбирают таким образом, чтобы обеспечить минимальное значение этой величины. Используя условия минимума (условие экстремума) для функции, зависящей от нескольких переменных. Мы получили систему уравнений для нахождения параметров 
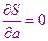
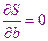
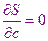 …..
…..
Мы получили систему, число уравнений которой равно числу параметров. 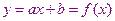
Наиболее часто экспериментальную зависимость аппроксимируют линейной функцией. В этом случае величина
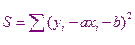
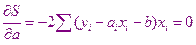
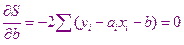
Перепишем полученную систему
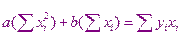
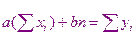
Получили систему двух уравнений с двумя неизвестными 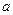 и
и 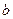 .
.
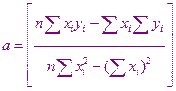
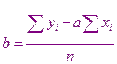
Аналогичным образом можно получить аппроксимирующую зависимость в виде полинома
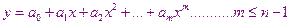
Метод наименьших квадратов можно использовать также при получении нелинейных двухпараметрических аппроксимирующих зависимостей. Вид аппроксимирующих зависимостей может быть заранее известен по некоторым, например физическим соображениям. Часто физическая зависимость имеет экспоненциальный вид:
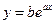 .
.
Эту зависимость можно привести к линейной с помощью следующих замен и преобразований:
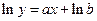 пусть
пусть
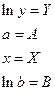
Тогда получим 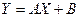
Имеющиеся у нас экспериментальные данные мы преобразовываем к следующему виду
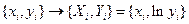
И теперь находим коэффициенты 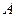 и
и 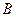 , а зная их мы можем вычислить
, а зная их мы можем вычислить 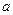 и
и 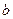 из следующих формул
из следующих формул
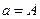 и
и 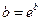
Построим таблицу позволяющую получать нелинейные аппроксимирующие зависимости.
Тема №3
Популярное:

