Определение ДУ. Решение ДУ. Задача Коши. Общее и частное решения. Геометрический смысл уравнения

Определение обыкновенного дифференциального уравнения (ОДУ) и его решения.

Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f ( x ) и её производных (или дифференциалов):

(1) (все три переменные x, y, F - действительны).

Опр. Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).
Пример: y ⁽⁴⁾ – y + x = 0 - уравнение четвёртого порядка.
Опр. Частным решением уравнения (1) на интервале ( a, b ) (конечном или бесконечном) называется любая n раз дифференцируемая функция 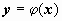, удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество. Так, функция y ( x ) = e^x + x обращает уравнение: y ⁽⁴⁾ – y + x = 0 в тождество на всей числовой оси ( y ⁽⁴⁾( x ) = e^x; e^x –( e^x + x ) + x = 0), т.е. является частным решением этого уравнения. Любое уравнение порядка имеет множество частных решений (частным решением приведённого уравнения является и функция y ( x ) = sin( x ) + x ). Процедуру решения дифференциального уравнения часто называют интегрированием уравнения, при этом интегрировать приходится в общем случае ровно n раз, и при каждом интегрировании в решение входит очередная произвольная постоянная.
Опр. Общим решением (общим интегралом) уравнения (1) называется такое соотношение

; (2)

что: 1. Любое решение (2) относительно y (для набора постоянных C ₁, C ₂, …, C_n из некоторой области n -мерного пространства) - частное решение уравнения (1);

2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C ₁, C ₂, …, C_n.
Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной:

; (3) и получать общее решение в форме (4)

решённой относительно неизвестной функции.

ОДУ первого порядка.

.Как следует из определения 14.1.1, обыкновенным дифференциальным уравнением первого порядка называется уравнение

(5) где x - независимая переменная, y ( x ) - неизвестная функция. В форме, разрешённой относительно производной, уравнение первого порядка записывается так:

(6)

Если пользоваться другим обозначением производной, то можно записать (6) как

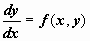(7)

Общее решение (общий интеграл) уравнения при n = 1 имеет вид или .
Геометрический смысл уравнения первого порядка. Уравнение (6) в каждой точке ( x, y ) области D, в которой задана функция f ( x, y ), определяет 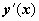- угловой коэффициент касательной к решению, проходящему через точку ( x, y ), т.е. направление, в котором проходит решение через эту точку. Говорят, что уравнение (6) задаёт в D поле направлений. График любого решения дифференциального уравнения (называемый также интегральной кривой ) в любой своей точке касается этого поля, т.е. проходит в направлении, определяемом полем. Интегрирование дифференциального уравнения геометрически означает нахождение кривых, у которых направление касательной в каждой точке совпадает с направлением поля. На рисунке справа изображено поле направлений, определяемое уравнением , и три интегральные кривые (три частных решения) этого уравнения. Решение можно провести через любую точку области D; единственное решение можно выделить, если задать точку, через которую проходит интегральная кривая:
.
Для изображения поля направлений, задаваемого дифференциальным уравнением, рассматривают линии уровня функции f ( x, y ), т.е. геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. С помощью изоклин можно приближённо изобразить интегральные кривые.
Для примера построим изоклины уравнения . Перебираем различные значения постоянной C, строим линии уровня функции 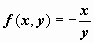, соответствующие этим значениям С (т.е. прямые ), и на этих линиях ставим чёрточки в направлении, определяемым значением С ( , где - угол между чёрточкой и положительным направлением оси Ох ): - ось Оу; ; ; и т.д. Информация о направлении интегральных кривых, полученная из рисунка (выше справа), достаточна, чтобы сделать качественный вывод об их поведении: кривые должны огибать начало координат. Это могут быть окружности или спирали (когда мы научимся решать дифференциальные уравнения, мы легко установим, что это окружности; две такие окружности изображены пунктиром).
Задача Коши (задача с начальным условием). Пусть функция f ( x, y ) определена в области D, точка 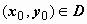. Требуется найти решение уравнения

(8)

удовлетворяющее начальному условию

y ( x ₀) = y ₀; (9)

(начальное условие (9) часто записывают в форме ).
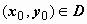Теорема Коши (существования и решения задачи Коши). Если в области D функция f ( x, y ) непрерывна и имеет непрерывную частную производную , то для любой точки в окрестности точки x ₀ существует единственное решение задачи ((8), (9)).
Мы примем эту теорему без доказательства. На самом деле для существования решения в окрестности точки x ₀ достаточно только непрерывности функции f ( x, y ); условие непрерывности обеспечивает единственность этого решения. 6

 

2. Решение уравнений с разделяющимися переменными, примеры

Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию

f ( x ) dx + g ( y ) dy = 0. (10)

Пусть y ( x ) - решение этого уравнения, т.е. f ( x ) dx + g ( y ( x )) dy ( x ) = 0. Интегрируя это тождество, получим - общий интеграл (общее решение) этого уравнения.
Пример: решить задачу Коши Исходное уравнение - с разделёнными переменными, интегрируя его, получим . Соотношение ( x -1)² + y ³ = C - общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x ₀ и y ₀, и найти значение постоянной C на этом решении: (2-1)² + 1³ = 2 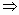C = 2. Таким образом, решение поставленной задачи: ( x -1)² + y ³ = 2.
Уравнения с разделяющимися переменными. Так называются уравнения вида

или (11)

f ₁( x ) g ₁( y ) dx + f ₂( x ) g ₂( y ) dy = 0 (12)

Эти уравнения легко сводятся к уравнению с разделёнными переменными:

Записываем уравнение (11) в форме , затем делим на g(y) и умножаем на dx: 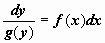.		Уравнение (12) делим на f2(x) g1(y): .
Эти уравнения - с разделёнными переменными. Интегрируя, получим общие интегралы:
.		.
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному.
Если функция g(y) имеет действительные корни y1, y2, y3, …, то функции y = y1, y = y2, y = y3, …, очевидно, являются решениями исходного уравнения.		Если функция f2(x) имеет действительные корни x1, x2, x3, …, функция g1(y) имеет действительные корни y1, y2, y3, …, то функции x = x1, x = x2, x = x3, …, y = y1, y = y2, y = y3, … являются решениями исходного уравнения.
В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши.

Примеры: 1. .
При такой форме записи общего интеграла решение y = 1 потеряно. Можно преобразовать общее решение к виду, который содержит это решение. Переобозначим постоянную C как ln| C ₁|: . Вернёмся к обозначению постоянной интегрирования C; общее решение содержит частное решение y = 1 при C = 0.
2. Найти решение задачи Коши
Решаем уравнение: . Здесь могут быть потеряны решения постоянная интегрирования записана как . Далее, . Общий интеграл уравнения

y ² = C ( x ² – 1) + 1. Частные решения содержатся в общем интеграле при C = 0, решения утеряны (понятно, почему это произошло: если записать уравнение в форме, решённой относительно производной, , то, очевидно, на решениях нарушаются условия, налагаемые теоремой Коши на правую часть уравнения). Всё множество решений: y ² = C ( x ² – 1) + 1, x = 1, x = -1. Мы должны найти ещё частное решение, удовлетворяющее начальному условию y (1) = 5. Подстановка значений x = 1, y = 5 в общий интеграл даёт 25=1, т.е. общий интеграл этого частного решения не содержит. Решение x = 1 удовлетворяет начальному условию, это и есть решение задачи Коши.

К уравнениям с разделяющимися переменными сводятся уравнения вида ( - постоянные). Если перейти к новой неизвестной функции z = ax + by + c, то , и уравнение представляется как 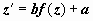. Это - уравнение с разделяющимися переменными.
Пример: .

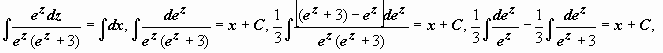
3. Однородные функции. Решение однородных ДУ первого порядка, примеры

⇐ Предыдущая12345678Следующая ⇒

Поделиться: