Семестр. ФНП. Кратные интегралы. Теория поля
Семестр. ФНП. Кратные интегралы. Теория поля
В каждой лекции все формулы, определения и теоремы нумеруются так же, как и в предыдущей лекции, с цифры 1 (т.е. нумерация не продолжается от лекции к лекции). Это удобно при чтении лекций.
Лекция 1. Множества в  мерном евклидовом пространстве и их типы. Функции нескольких переменных, их предел и непрерывность. Линии и поверхности уровня. Частные производные и их геометрический смысл. Дифференцируемость и её связь с частными производными функции
мерном евклидовом пространстве и их типы. Функции нескольких переменных, их предел и непрерывность. Линии и поверхности уровня. Частные производные и их геометрический смысл. Дифференцируемость и её связь с частными производными функции
Напомним сначала некоторые сведения из теории метрических пространств.
Метрические пространства. Открытые и замкнутые множества. Понятие области
В предыдущих лекциях вводилось понятие евклидова пространства, т.е. пространства 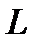 со скалярным произведением
со скалярным произведением  (
(  ). Введем теперь в рассмотрение понятие метрического пространства.
). Введем теперь в рассмотрение понятие метрического пространства.
Определение 1. Линейное пространство  называется метрическим пространством, если в нем для любых векторов
называется метрическим пространством, если в нем для любых векторов 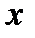 и
и  определено число
определено число  называемое расстоянием между
называемое расстоянием между 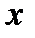 и
и  (или метрикой в
(или метрикой в  ), обладающее следующими свойствами:
), обладающее следующими свойствами:
1. П.О. 
2. С. 
3. Т. 
 (
(  произвольные векторы из пространства
произвольные векторы из пространства 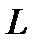 ).
).
Любое евклидово пространство 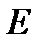 является одновременно и метрическим пространст-
является одновременно и метрическим пространст-
вом с метрикой  (проверьте выполнение свойств 1-3). Заметим, что число
(проверьте выполнение свойств 1-3). Заметим, что число 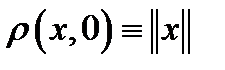 называется длиной (или нормой) вектора
называется длиной (или нормой) вектора  Так что
Так что 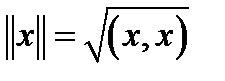 в евкли-
в евкли-
довом пространстве  Например, в
Например, в  мерном точечном евклидовом пространстве
мерном точечном евклидовом пространстве  метрика вводится следующим образом:
метрика вводится следующим образом:


В любом метрическом пространстве  можно ввести понятие окрестности точки. Если
можно ввести понятие окрестности точки. Если
 фиксированная точка метрического пространства
фиксированная точка метрического пространства  то множество
то множество

называется  окрестностью точки
окрестностью точки 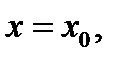 а множество
а множество  –
–
проколотой  окрестностью этой точки.
окрестностью этой точки.
Мы будем работать в основном с евклидовыми пространствами 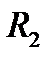 и
и 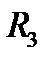 , поэтому дадим описание в них
, поэтому дадим описание в них  окрестности точки (см. (1)):
окрестности точки (см. (1)):
в пространстве  открытый круг радиуса
открытый круг радиуса  (см. Р.1);
(см. Р.1);
в пространстве 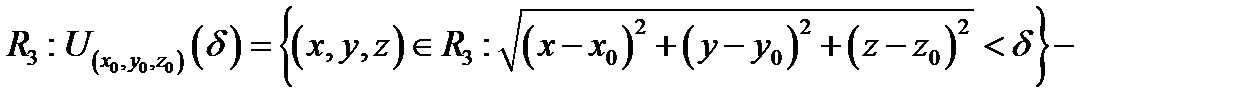 откры-
откры-
 тый шар радиуса
тый шар радиуса 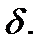
Введем теперь понятие внутренней и граничной точки множества  метрического пространства
метрического пространства  Точка
Точка  называется внутренней точкой множества
называется внутренней точкой множества 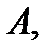 если она входит в
если она входит в  вместе с некоторой своей окрестностью. Точка
вместе с некоторой своей окрестностью. Точка  называется граничной точкой множества
называется граничной точкой множества  если в любой окрестности этой точки существуют точки, как принадлежащие
если в любой окрестности этой точки существуют точки, как принадлежащие  так и не принадлежащие
так и не принадлежащие 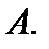 Множество всех граничных точек множества
Множество всех граничных точек множества  образуют границу
образуют границу  которая обозначается символом
которая обозначается символом  или
или 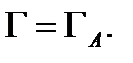 Можество
Можество  называется открытым множеством, если все его точки внутренние. Если множеству
называется открытым множеством, если все его точки внутренние. Если множеству  принадлежат все его граничные точки, то оно называется замкнутым множеством. Точка
принадлежат все его граничные точки, то оно называется замкнутым множеством. Точка  называется предельной точкой множества
называется предельной точкой множества 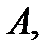 если в любой окрестности этой точки существует точка
если в любой окрестности этой точки существует точка 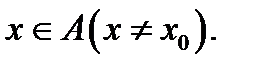
Теперь введем понятие области. При этом везде ниже рассматривается только евклидово пространство 
 мерных упорядочных точек
мерных упорядочных точек  с метрикой (1). Заметим сначала, что множество
с метрикой (1). Заметим сначала, что множество  называется связным, если любые две его точки можно соединить непрерывной кривой, не выходящей из
называется связным, если любые две его точки можно соединить непрерывной кривой, не выходящей из 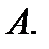 И наконец, любое связное открытое множество в
И наконец, любое связное открытое множество в  называется областью.
называется областью.
Лекция 2. Дифференцирование сложной функции. Неявная функция и её дифференцирова-
Ние. Частные производные и дифференциалы высших порядков. Равенство смешанных производных. Скалярное поле. Градиент и его связь с производной поля по направлению
Если даны функции
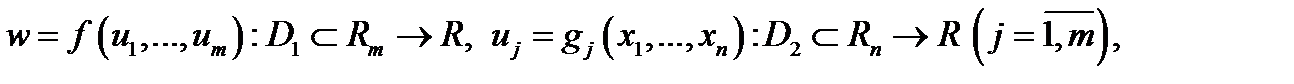
то можно образовать сложную функцию  При этом областью определения сложной функции будет множество
При этом областью определения сложной функции будет множество  таких
таких  что выражение
что выражение 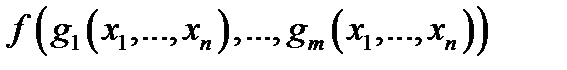 имеет смысл. Мы будем рассматривать в основном сложные функции вида
имеет смысл. Мы будем рассматривать в основном сложные функции вида  и
и  . Все утверждения, сформулированные для таких функций, очевидным образом переносятся и на общие типы сложных функций.
. Все утверждения, сформулированные для таких функций, очевидным образом переносятся и на общие типы сложных функций.
Лекция 3. Касательная плоскость и нормаль к поверхности. Локальный экстремум функции нескольких переменных, необходимое условие экстремума. Достаточные условия существования экстремума. Наибольшее и наименьшее значения функции на замкнутом ограниченном множестве. Условный экстремум и метод множителей Лагранжа
Прежде чем перейти к изложению следующего раздела, отметим, что кривую в пространстве  можно задать системой уравнений
можно задать системой уравнений
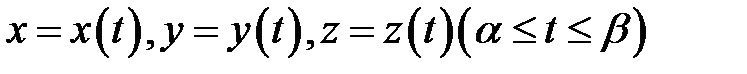 .
. 
 Действительно, при изменении параметра
Действительно, при изменении параметра 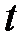 на отрезке
на отрезке 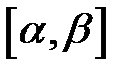 точка
точка 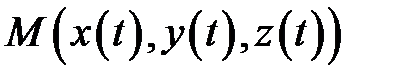 описывает в
описывает в 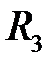 некоторую кривую
некоторую кривую 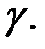 При этом кривая
При этом кривая 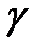 называется непрерывной, если все функции непрерывны на отрезке
называется непрерывной, если все функции непрерывны на отрезке 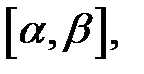 и
и 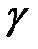 называется гладкой кривой, если производные
называется гладкой кривой, если производные 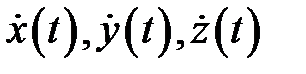 непрерывны на указанном отрезке. Точка
непрерывны на указанном отрезке. Точка 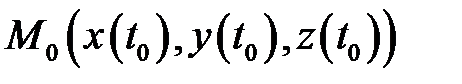 называется неособой, если
называется неособой, если 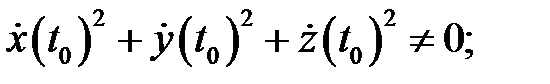 в противном случае (т.е. в случае
в противном случае (т.е. в случае 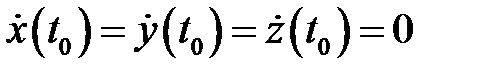 )точка
)точка 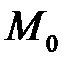 называется особой. Нетрудно показать, что вектор
называется особой. Нетрудно показать, что вектор 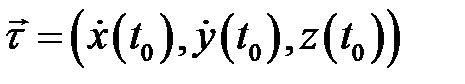 является касательным вектором к кривой
является касательным вектором к кривой 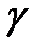 в точке
в точке 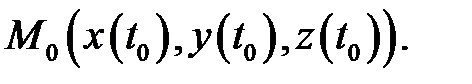
Решение.
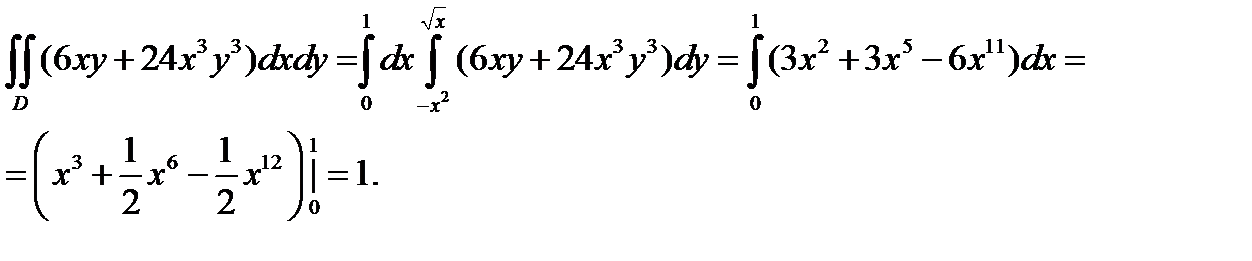
Немного позже будет использоваться формула
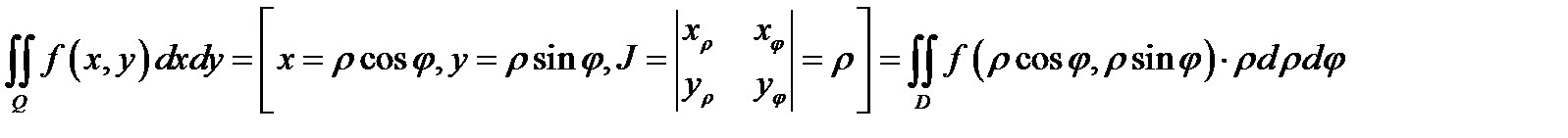
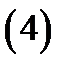
вычисления двойного интеграла в полярных координатах. Этой формулой удобно пользоваться в тех случаях, когда область  при отображении
при отображении 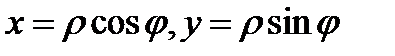 переходит в прямоугольник или в какую-нибудь другую простую область.
переходит в прямоугольник или в какую-нибудь другую простую область.
Пример 3. Вычислить интеграл
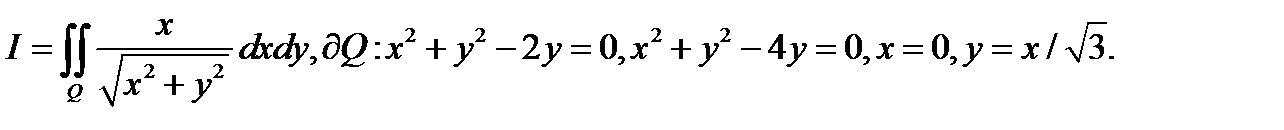
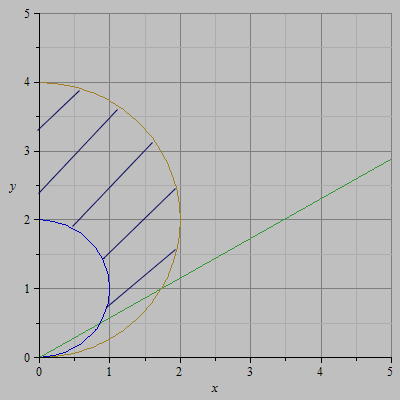 Решение. Здесь область
Решение. Здесь область 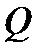 находится в первой четверти между двумя окружностями и двумя прямыми
находится в первой четверти между двумя окружностями и двумя прямыми 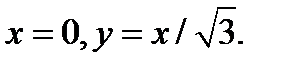 После преоб-
После преоб-
разования 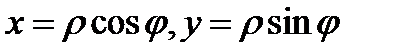 она переходит в область
она переходит в область 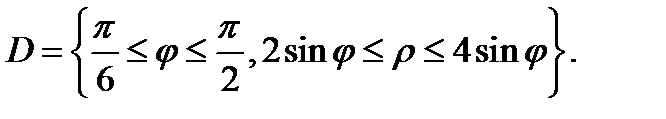 Согласно формуле (4) имеем
Согласно формуле (4) имеем
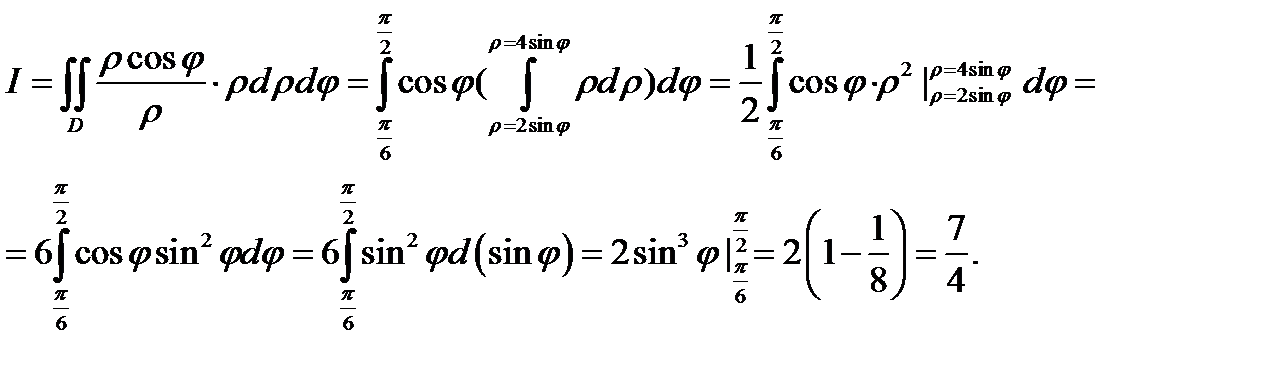
Лекция 5. Замена переменных в кратных интегралах. Якобиан и его геометрический смысл. Полярные, цилиндрические и сферические координаты в двойных и тройных интегралах. Площадь поверхности и её вычисление
Ранее упоминалось, что некоторые двойные интегралы удобно вычислять в полярных координатах. В отличие от прямоугольных декартовых координат полярные координаты являются криволинейными. Перейдем к описанию криволинейных координат общего вида.
 1. Криволинейные координаты на плоскости
1. Криволинейные координаты на плоскости
Пусть в плоскости 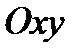 задана некоторая область
задана некоторая область  а в плоскости
а в плоскости  некоторая область
некоторая область 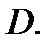
Определение 1. Говорят, что функции



задают взаимно однозначное соответствие
области 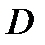 на область
на область  если каждой точке
если каждой точке  соответствует единственная точка
соответствует единственная точка 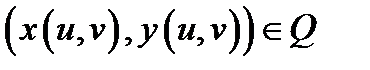 и двум различным точкам из области
и двум различным точкам из области  соответствуют две различные точки из области
соответствуют две различные точки из области  по закону (1).
по закону (1).
Ясно, что в этом случае существует и обратное отображение  , задаваемое некоторыми функциями
, задаваемое некоторыми функциями 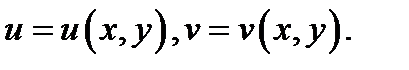 Если (1) задаёт взаимно однозначное соответствие
Если (1) задаёт взаимно однозначное соответствие  то положение любой точки
то положение любой точки 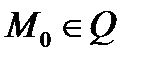 фиксируется её декартовыми координатами
фиксируется её декартовыми координатами  или парой чисел
или парой чисел  такой, что
такой, что 
Определение 2. Пара  только что описанныхчисел называется криволинейными координатами точки
только что описанныхчисел называется криволинейными координатами точки 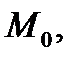 а кривые
а кривые

называются координатными линиями точки 
Таким образом, в области  можно задать две системы координат: 1) декартову прямоугольную систему координат, определяемую сеткой взаимно ортогональных прямых
можно задать две системы координат: 1) декартову прямоугольную систему координат, определяемую сеткой взаимно ортогональных прямых  и криволинейную систему координат, определяемую сеткой координатных линий
и криволинейную систему координат, определяемую сеткой координатных линий 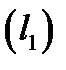 и
и 
Определение 3. Определитель  называется якоби-
называется якоби-
аном отображения (1) или якобианом перехода от декартовых координат к криволинейным.
Можно показать, что  равен коэффициенту искажения площадей (геометрический смысл якобиана), т.е. если
равен коэффициенту искажения площадей (геометрический смысл якобиана), т.е. если 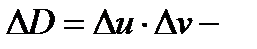 площадь малого прямоугольника с одной из вершин
площадь малого прямоугольника с одной из вершин  и ребрами
и ребрами 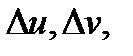 а
а  площадь криволинейного четырёхугольника, являющегося образом указанного прямоугольника при отображении (1), то
площадь криволинейного четырёхугольника, являющегося образом указанного прямоугольника при отображении (1), то 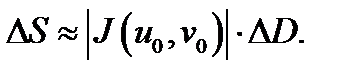 Используя этот факт, можно доказать следующее утверждение.
Используя этот факт, можно доказать следующее утверждение.
Теорема 1. Имеет место равенство
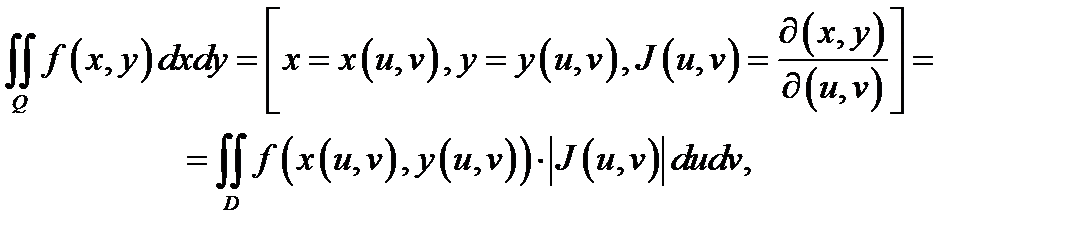
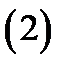
если выполнены следующие условия:
1) функция  непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 
2) функции 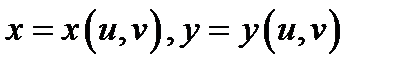 непрерывно дифференцируемы в области
непрерывно дифференцируемы в области 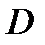 и взаимно однозначно отображают область
и взаимно однозначно отображают область 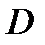 на область
на область 
3) якобиан 
Площадь поверхности

Пусть в пространстве 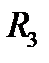 задана некоторая гладкая поверхность
задана некоторая гладкая поверхность  и пусть
и пусть 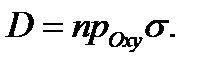 Произведем разбиение
Произведем разбиение
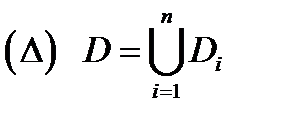 области
области 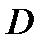 на частичные подобласти
на частичные подобласти 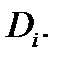 Это разбиение индуцирует разбиение
Это разбиение индуцирует разбиение 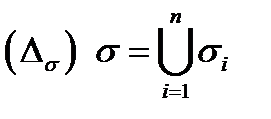 поверхности
поверхности  на частичные поверхности
на частичные поверхности 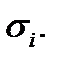 Возьмем произвольно точку
Возьмем произвольно точку 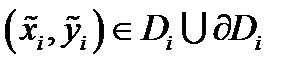 и в соответствующей точке
и в соответствующей точке 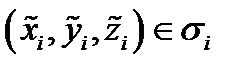 построим плоскость
построим плоскость 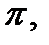 касательную к поверхности
касательную к поверхности 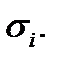 Цилиндр с основанием
Цилиндр с основанием 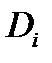 и образующей, параллельной оси
и образующей, параллельной оси 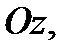 вырежит из этой плоскости кусок
вырежит из этой плоскости кусок 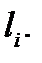 Обозначим через
Обозначим через 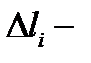 площадь куска
площадь куска 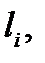 а через
а через 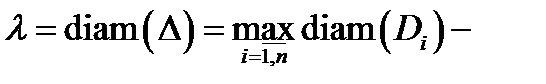 диаметр разбиения
диаметр разбиения 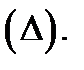
Определение 4. Если существует конечный предел 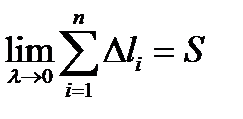 и он не зависит от вида разбиения
и он не зависит от вида разбиения 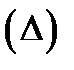 и выбора точек
и выбора точек 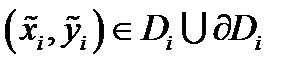 , то его называют площадью поверхности
, то его называют площадью поверхности 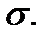
Теорема 3. Пусть поверхность  задаётся уравнением
задаётся уравнением 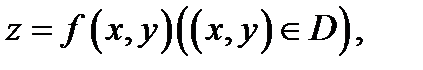 причем функция
причем функция 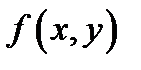 и её частные производные
и её частные производные 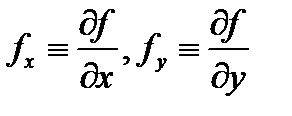 непрерывны в замкнутой ограниченной области
непрерывны в замкнутой ограниченной области 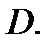 Тогда площадь поверхности
Тогда площадь поверхности  вычисляется по формуле
вычисляется по формуле
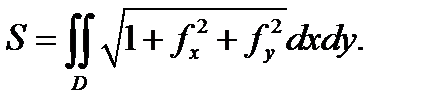
Доказательство. Вычислим площадь 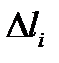 куска
куска 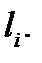 Так как
Так как 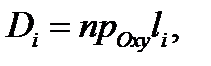 то
то 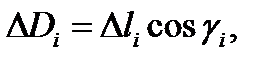
где 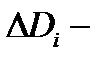 площадь области
площадь области 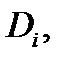 а
а 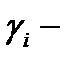 угол между плоскостями
угол между плоскостями 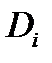 и
и 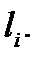 Угол
Угол 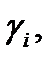 очевидно, равен углу между нормалями
очевидно, равен углу между нормалями 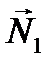 и
и 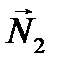 плоскостей
плоскостей 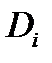 и
и 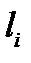 соответсвенно. Так как
соответсвенно. Так как 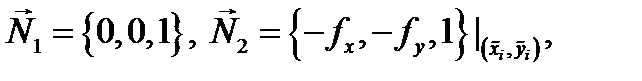 то
то
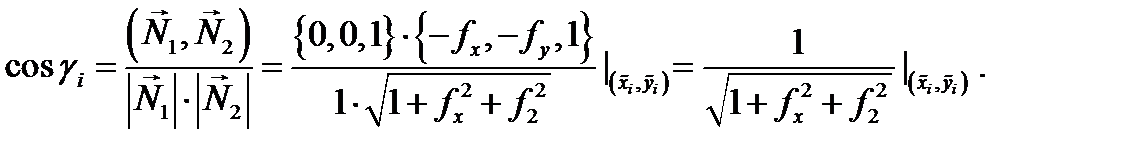
Следовательно, 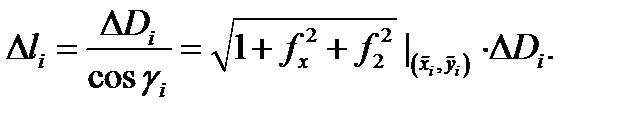 По определению 4 имеем
По определению 4 имеем
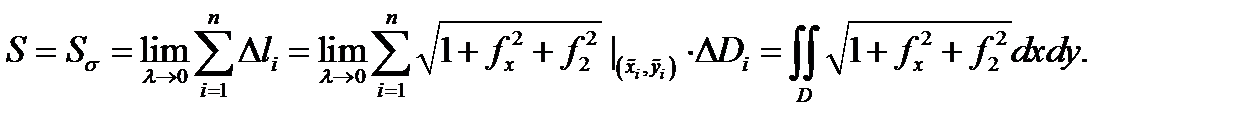
Теорема доказана.
Пример 3. Вычислить площадь части поверхности параболоида 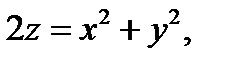 вырезан-
вырезан-
ную цилиндром 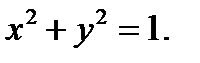
Решение. Здесь область 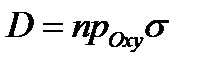 есть круг
есть круг 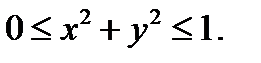 Площадь искомой поверхнос-
Площадь искомой поверхнос-
ти  находим по формуле (8):
находим по формуле (8):
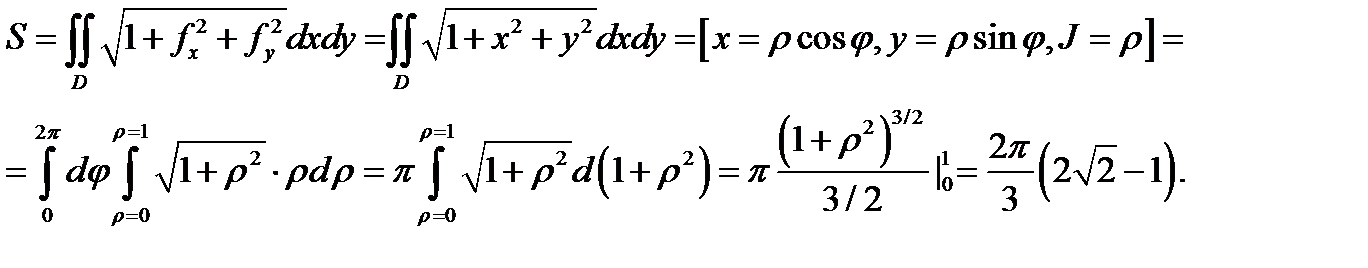
Лекция 6. Поверхностный интеграл первого рода (по площади поверхности) и его вычисление. Векторное поле. Векторные линии векторные трубки. Поток векторного поля, его свойства и вычисление. Дивергенция, её физический смысл и свойства. Формула Остроградского-Гаусса
Поверхностный интеграл
 Пусть в пространстве переменных
Пусть в пространстве переменных 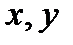 и
и 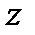 задана некоторая поверхность
задана некоторая поверхность  и пусть функция
и пусть функция 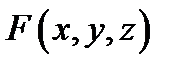 определена на этой поверхности. Произведём разбиение
определена на этой поверхности. Произведём разбиение 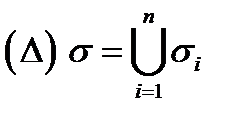 поверхности
поверхности  на частичные поверхности
на частичные поверхности 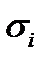 с помощью конечного числа непрерывных кривых. Возьмём произвольно точки
с помощью конечного числа непрерывных кривых. Возьмём произвольно точки 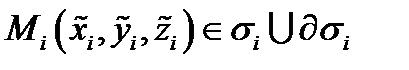 и составим интегральную сумму
и составим интегральную сумму 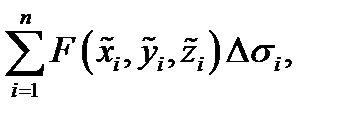 где
где 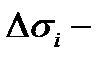 площадь куска
площадь куска 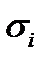 . Обозначим
. Обозначим 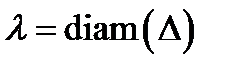 .
.
Определение 1. Если существует предел интегральных сумм: 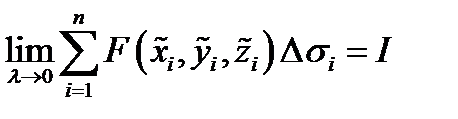 и если этот предел не зависит от вида разбиения
и если этот предел не зависит от вида разбиения 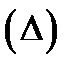 и выбора точек
и выбора точек 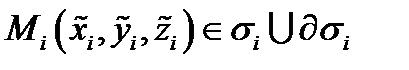 , то его называют поверхностным интегралом первого рода от функции
, то его называют поверхностным интегралом первого рода от функции 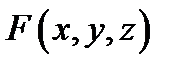 по поверхности
по поверхности  и обозначают
и обозначают 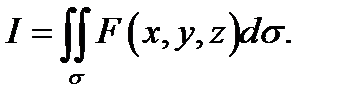
Теорема 1. Если поверхность  задана уравнением
задана уравнением 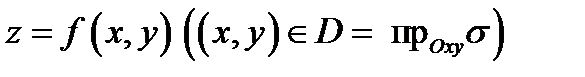 и функции
и функции
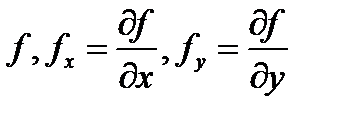 непрерывны в замкнутой ограниченной области
непрерывны в замкнутой ограниченной области 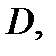 а функция
а функция 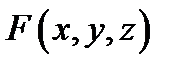 непрерывна на поверхности
непрерывна на поверхности 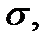 то
то
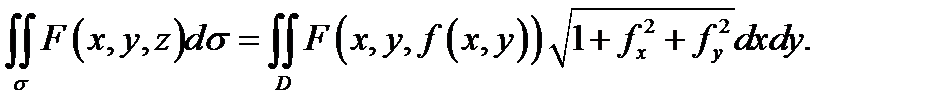
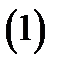
Доказательство следует из равенства
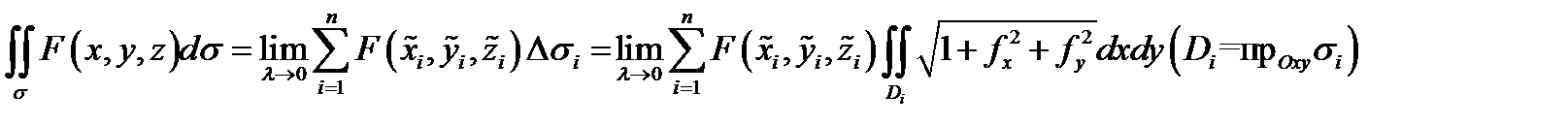
и теоремы о среднем 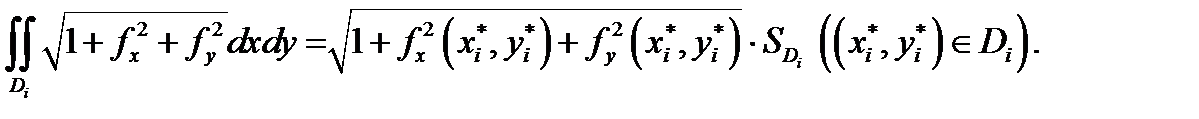 Подставляя это в предыдущее равенство и учитывая непрерывность всех функций, будем иметь
Подставляя это в предыдущее равенство и учитывая непрерывность всех функций, будем иметь
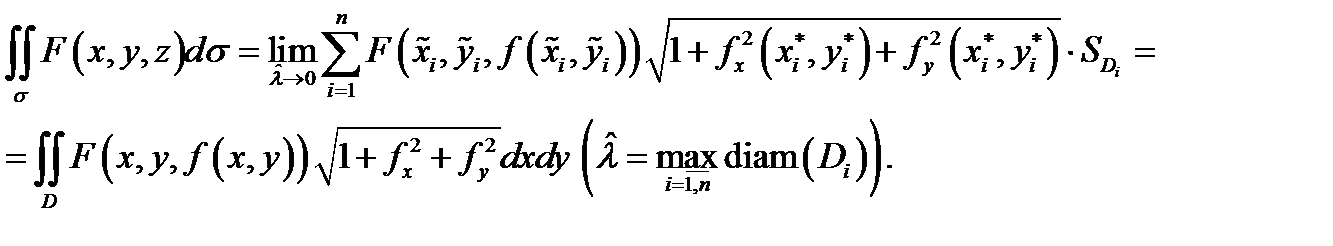
Теорема доказана.
Так как поверхностный интеграл сводится к двойному, то для него справедливы все свойства последнего: линейность, аддитивность, монотонность, теорема о среднем и т.д. Мы не будем их выписывать. Механический смысл поверхностного интеграла состоит в следующем: если 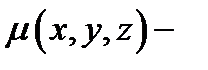 плотность пластинки
плотность пластинки  в точке
в точке 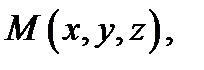 то
то 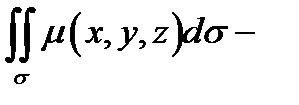 масса этой пластинки.
масса этой пластинки.
2. Векторное поле. Векторные линии векторные трубки. Ориентируемые поверхности и поток векторного поля через поверхность
Пусть 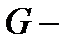 некоторая область в пространстве
некоторая область в пространстве 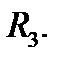
Определение 2. Говорят, что в области 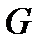 задано векторное поле
задано векторное поле 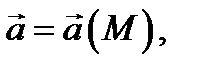 если в каждой точке
если в каждой точке 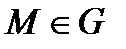 определен вектор
определен вектор 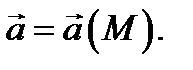
Это определение не зависит от выбора системы координат в 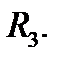 Если в
Если в 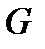 выбрана декартова система координат, то каждой точке
выбрана декартова система координат, то каждой точке 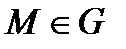 ставится в соответствие вектор
ставится в соответствие вектор
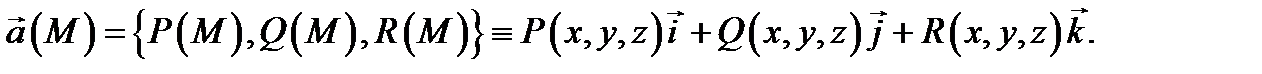
Примеры векторных полей: а) 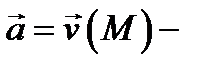 скорость движущейся жидкости в точке
скорость движущейся жидкости в точке 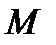 (векторное полей скоростей жидкости); б)
(векторное полей скоростей жидкости); б) 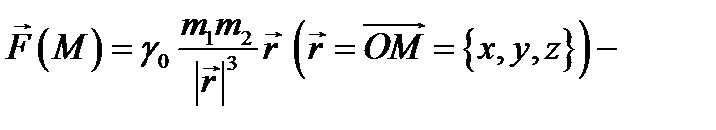 гравитационное поле (здесь тело массой
гравитационное поле (здесь тело массой 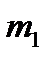 находится в точке
находится в точке 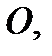 а тело массой
а тело массой 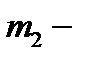 в точке
в точке 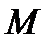 ,
, 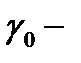 гравитационная постоянная).
гравитационная постоянная).
Векторное поле 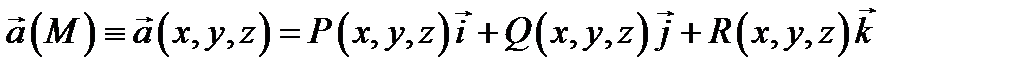 называеется непрерывным (кусочно непрерывным, гладким, непрерывно дифференцируемым) в области
называеется непрерывным (кусочно непрерывным, гладким, непрерывно дифференцируемым) в области 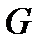 , если все его компоненты
, если все его компоненты 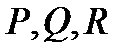 непрерывны (соответственно: кусочно непрерывны, гладки, непрерывно дифференцируемы) в области
непрерывны (соответственно: кусочно непрерывны, гладки, непрерывно дифференцируемы) в области 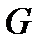 .
.
Пусть векторное поле 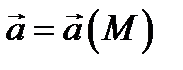 определено в области
определено в области  .
.
Определение 3. Линия  называется векторной линией поля
называется векторной линией поля 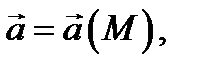 если в каждой точке
если в каждой точке 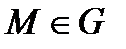 поле
поле 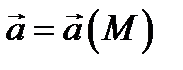 касается кривой
касается кривой 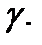 Поверхность
Поверхность 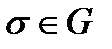 называется векторной трубкой поля
называется векторной трубкой поля 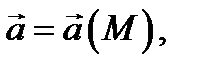 если она сплошь состоит из векторных линий этого поля.
если она сплошь состоит из векторных линий этого поля.
Теорема 2. Пусть поле 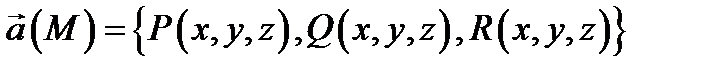 непрерывно дифференци-
непрерывно дифференци-
руемо в области 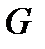 . Если
. Если 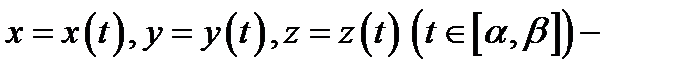 параметрические уравнения векторной линии поля
параметрические уравнения векторной линии поля 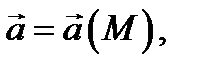 то для всех
то для всех 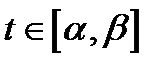 выполняются равенства
выполняются равенства
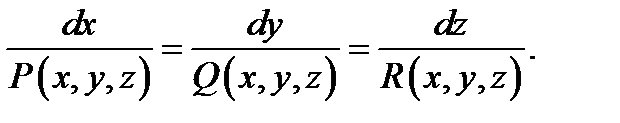
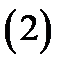
Обратно: если кривая 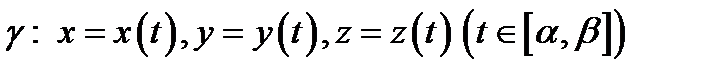 удовлетворяет соотношени-
удовлетворяет соотношени-
ям (1), то 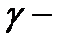 векторная линия поля
векторная линия поля 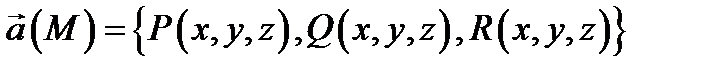 (уравнения (2) называются уравнениями векторных линий поля
(уравнения (2) называются уравнениями векторных линий поля 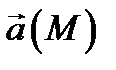 ).
).
Действительно, равенства (2) (если в них подставить уравнения 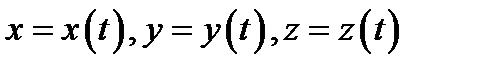
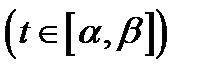 линии
линии 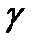 ) выражают условия коллинеарности векторов
) выражают условия коллинеарности векторов 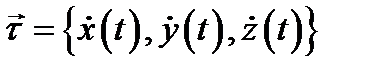 и
и 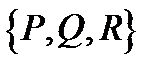 в одной и той же точке
в одной и той же точке 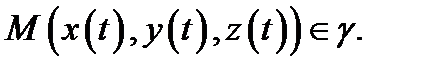 Значит, линия
Значит, линия 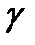 касается поля
касается поля 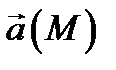 .
.
 Пусть в пространстве задана некоторая поверхность
Пусть в пространстве задана некоторая поверхность  и пусть в каждой точке
и пусть в каждой точке 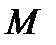 этой поверхности существует нормаль. На этой нормали можно выбрать два единичных вектора:
этой поверхности существует нормаль. На этой нормали можно выбрать два единичных вектора: 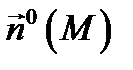 и
и 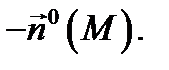
Определение 4. Если при движении точки  по любому замкнутому контуру, лежащему на поверхности
по любому замкнутому контуру, лежащему на поверхности  и не пересекающему её границы
и не пересекающему её границы 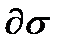 , единичный вектор
, единичный вектор 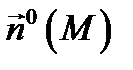 непрерывно изменяется и возвращается в точку
непрерывно изменяется и возвращается в точку 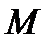 с первоначальным направлением, то говорят, что поверхность
с первоначальным направлением, то говорят, что поверхность  яв-
яв-
ляется двухсторонней. При этом сторона поверхности, определяемая вектором 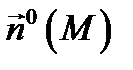 , называется внешней (или верхней) стороной поверхности
, называется внешней (или верхней) стороной поверхности  (обозначение:
(обозначение: 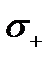 ), а сторона поверхности, определяемая вектором
), а сторона поверхности, определяемая вектором 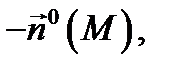 называется внутренней (или нижней) стороной поверхности
называется внутренней (или нижней) стороной поверхности  (обозначение:
(обозначение: 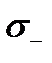 ). Векторы
). Векторы 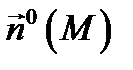 и
и 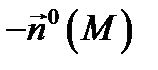 называются ориентациями поверхности
называются ориентациями поверхности  , а сама поверхность
, а сама поверхность  называется ориентируемой поверхностью.
называется ориентируемой поверхностью.
Если же на поверхности  найдётся хотя бы один замкнутый контур, при движении на котором единичный вектор
найдётся хотя бы один замкнутый контур, при движении на котором единичный вектор 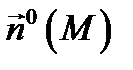 возвращается в точку
возвращается в точку 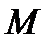 с противоположным направлением, то говорят, что поверхность
с противоположным направлением, то говорят, что поверхность  является односторонней или неориентируемой
является односторонней или неориентируемой
поверхностью.
Примером неориентируемой поверхности является лист Мёбиуса, который получается из прямоугольной полоски склеванием ее боковых после однократного их перекручивания. Перейдем к понятию потока векторного поля. Пусть дана двухсторонняя поверхность  и выбрана та её сторона, которая ориентирована единичной нормалью
и выбрана та её сторона, которая ориентирована единичной нормалью 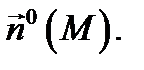
Определение 4. Потоком векторного поля 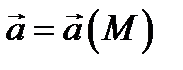 через поверхность
через поверхность  с ориентацией
с ориентацией 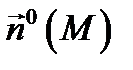 называется поверхностный интеграл
называется поверхностный интеграл
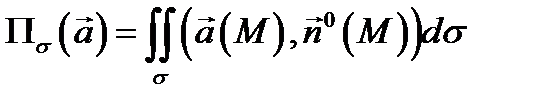
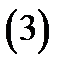
(здесь 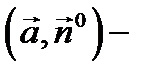 скалярное произведение векторов
скалярное произведение векторов 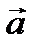 и
и 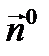 ).
).
Это определение потока не зависит от выбора системы координат. Если выбрана прямоугольная система координат, то
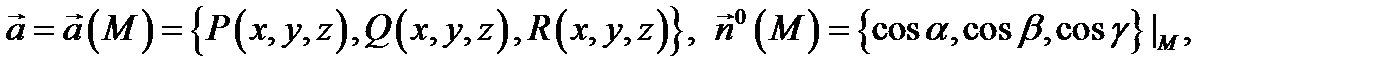
и поток можно записать в виде 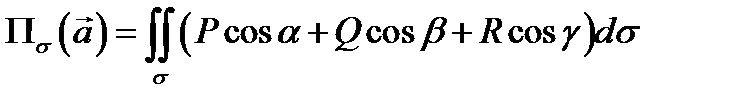 . Обозначив
. Обозначив
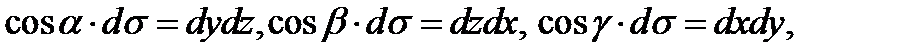 перепишем предыдущее равенство в виде
перепишем предыдущее равенство в виде
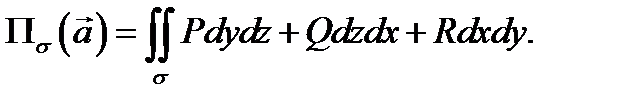 В таком виде поток записан в форме поверхностного интеграла второго рода (по координатам). Все три формы записи потока встречаются в математической литературе. Мы будем пользоваться первой формой записи, указанной в определении 4.
В таком виде поток записан в форме поверхностного интеграла второго рода (по координатам). Все три формы записи потока встречаются в математической литературе. Мы будем пользоваться первой формой записи, указанной в определении 4.
Из свойств поверхностного интеграла первого рода вытекают аналогичные свойства потока как поверхностного интеграла второго рода (линейность, аддитивность и т.д). Единственным отличием этих свойствах является то, что интеграл первого рода не зависит от ориентации поверхности  а интеграл второго рода (поток) зависит от выбора стороны поверхности:
а интеграл второго рода (поток) зависит от выбора стороны поверхности: 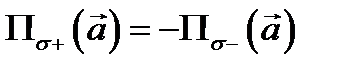 (это вытекает из определения 4). Дадим формулу вычисления потока.
(это вытекает из определения 4). Дадим формулу вычисления потока.
Теорема 3. Пусть 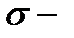 поверхность, задаваемая уравнением
поверхность, задаваемая уравнением 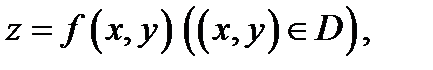 причем эта поверхность является гладкой, т.е. функции
причем эта поверхность является гладкой, т.е. функции 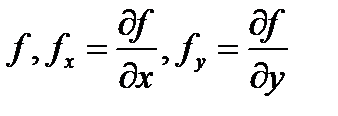 непрерывны в замкнутой ограниченной области
непрерывны в замкнутой ограниченной области 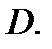 Пусть, кроме того, векторное поле
Пусть, кроме того, векторное поле 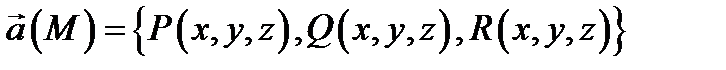 непрерывно на поверхности
непрерывно на поверхности 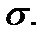 Тогда
Тогда
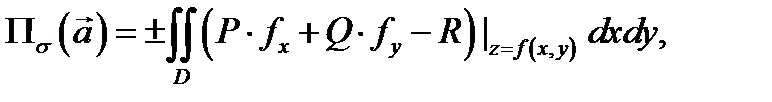
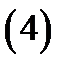
где знак (+) отвечает ориентации поверхности  нормальным вектором
нормальным вектором 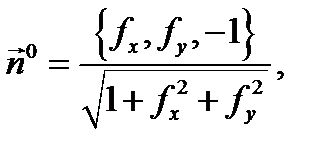 а знак (–) отвечает ориентации поверхности
а знак (–) отвечает ориентации поверхности  нормальным вектором
нормальным вектором 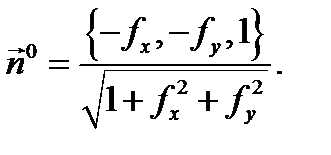
Доказательство. Пусть поверхность  ориентирована вектором
ориентирована вектором 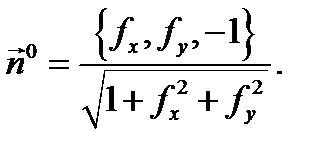 Учитывая, что
Учитывая, что 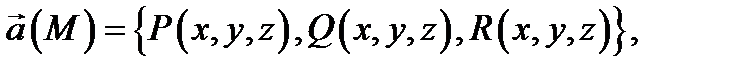 раскроем в (3) скалярное произведение:
раскроем в (3) скалярное произведение: 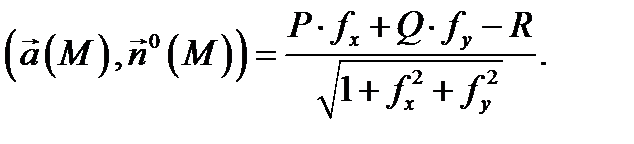 По теореме 1 имеем
По теореме 1 имеем
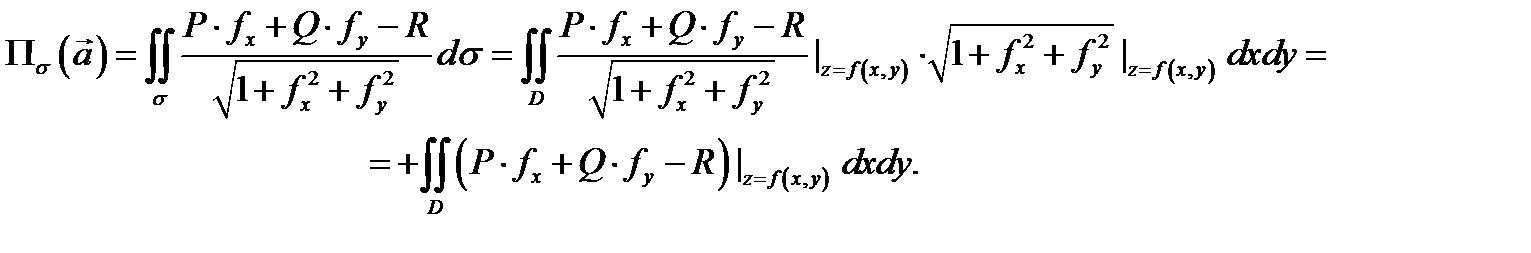
Теорема доказана.
Замечание 1. Если поверхность  задана неявно уравнением
задана неявно уравнением 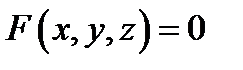 (где функции
(где функции 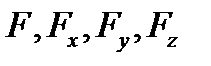 непрерывны, причем
непрерывны, причем 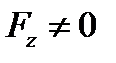 в области
в области 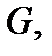 в которой лежит поверхность
в которой лежит поверхность  ), то
), то
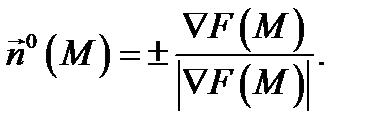 При этом знак выбирается в соответствии с ориентацией поверхности
При этом знак выбирается в соответствии с ориентацией поверхности  .
.
Дадим гидромеханический смысл потока: если 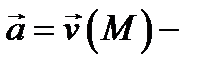 векторное поле скоростей жидкости, то
векторное поле скоростей жидкости, то 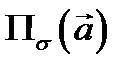 равен количеству жидкости, протекающей за единицу времени через поверхность
равен количеству жидкости, протекающей за единицу времени через поверхность  с ориентацией, определяемой нормалью
с ориентацией, определяемой нормалью 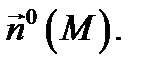
Пример 1 ( Кузнецов Л.А. Типовые расчеты ). Найти поток векторного поля 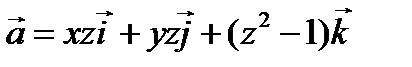 через поверхность
через поверхность 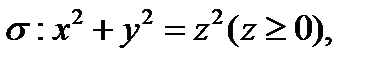 вырезаемую плоскостью
вырезаемую плоскостью 
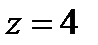 (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
(нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
Решение. Так как 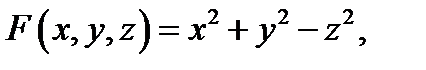 то нормаль к боковой поверхности
то нормаль к боковой поверхности  (конуса) будет иметь вид
(конуса) будет иметь вид 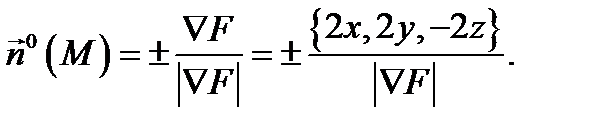 Выбор нормали должен быть таким, чтобы
Выбор нормали должен быть таким, чтобы 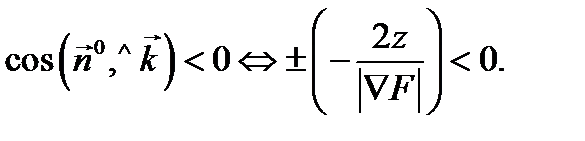 Так как в нашем случае
Так как в нашем случае 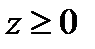 на поверхности
на поверхности  , то надо взять знак (+). Таким образом, нормаль будет такой:
, то надо взять знак (+). Таким образом, нормаль будет такой: 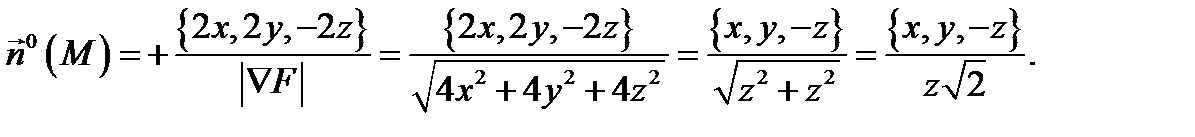 Здесь мы учли, что на поверхности
Здесь мы учли, что на поверхности  выполняется равенство
выполняется равенство 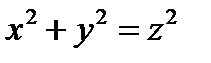 . Далее имеем
. Далее имеем
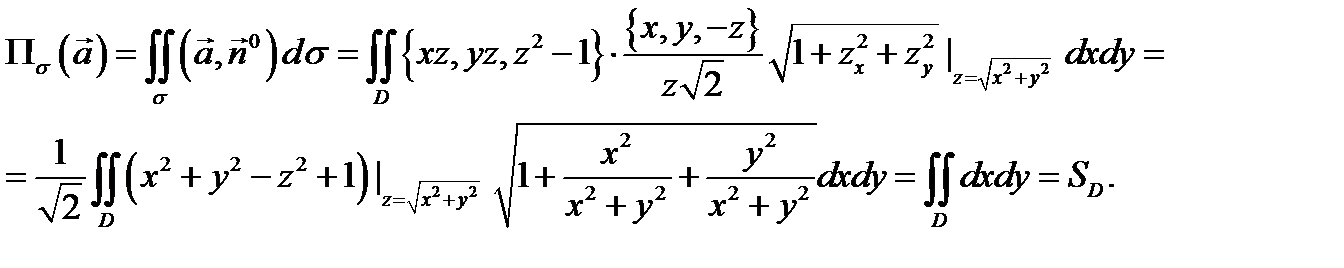
Область 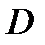 является проекцией поверхности
является проекцией поверхности  на плоскость
на плоскость 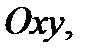 т.е. является кругом радиуса
т.е. является кругом радиуса 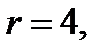 поэтому
поэтому 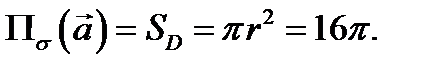
семестр. ФНП. Кратные интегралы. Теория поля
В каждой лекции все формулы, определения и теоремы нумеруются так же, как и в предыдущей лекции, с цифры 1 (т.е. нумерация не продолжается от лекции к лекции). Это удобно при чтении лекций.
Лекция 1. Множества в  мерном евклидовом пространстве и их типы. Функции нескольких переменных, их предел и непрерывность. Линии и поверхности уровня. Частные производные и их геометрический смысл. Дифференцируемость и её связь с частными производными функции
мерном евклидовом пространстве и их типы. Функции нескольких переменных, их предел и непрерывность. Линии и поверхности уровня. Частные производные и их геометрический смысл. Дифференцируемость и её связь с частными производными функции
Напомним сначала некоторые сведения из теории метрических пространств.

