Достаточные признаки существования экстремумов. Выпуклость вверх и вниз графика функции. Асимптоты

1. Первый и второй достаточные признаки существования экстремума.

Первый достаточный признак существования экстремума дается теоремой:

Т1. Если функция дифференцируема в некоторой окрестности точки , кроме может быть самой точки , и при переходе через эту точку слева направо ее первая производная меняет свой знак с “+” на “–”, то в точке функция имеет максимум, а если ее первая производная меняет свой знак с “–” на “+”, то в точке функция имеет минимум. Если при переходе через точку первая производная не меняет свой знак, то в этой точке экстремума нет.

Второй достаточный признак существования экстремума дается теоремой:

Т2. Если в точке первая производная функции обращается в ноль ( 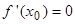), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке (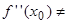 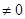), то в точке наблюдается экстремум. Если при этом 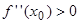, то точка является точкой минимума, а при 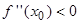– точкой максимума.

Пример 1. Найти и определить тип экстремумов функции .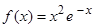

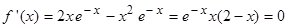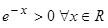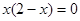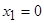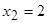Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек: . Так как показательная функция , то . Отсюда находим критические точки и . Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:

– + –

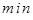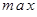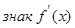
0 2

При переходе слева направо через точку 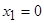первая производная функция меняет свой знак с “–” на “+”, следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку 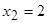первая производная функция меняет свой знак с “+” на “–”, следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции: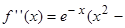 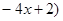. Вычислим значение второй производной функции в точке 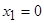: 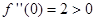, следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке 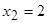: 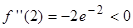, следовательно, в этой точке функция имеет максимум.

2. Наименьшее и наибольшее значения функции на отрезке .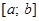

Пусть функция непрерывна на отрезке 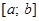и имеет конечное число точек экстремума на этом интервале. Если наибольшее значение функция достигает внутри отрезка, то очевидно, что это будет один из максимумов (аналогично для наименьшего значения – один из минимумов). Однако возможны варианты, когда функция достигает своих наименьшего и наибольшего значений на концах заданного отрезка. Поэтому для отыскания этих значений применяют следующую схему:

1. Находят область определения функции и убеждаются в том, что заданный отрезок входит в эту область.

2. Находят критические точки, для чего решают уравнение 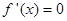, и точки, в которых первая производная функции не существует.

3. Вычисляют значения функции в критических точках, принадлежащих заданному отрезку, в точках, в которых первая производная функции не существует и на концах заданного отрезка.

4. Из полученных чисел выбирают наименьшее 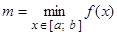и наибольшее .

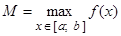Пример 2. Найти наименьшее и наибольшее значения функции 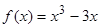на отрезке .

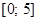Действуя согласно вышеприведенной схеме, находим:

1. 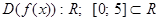. Следовательно, функция определена и непрерывна на заданном отрезке.

2. Вычислим первую производную 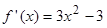. Производная существует на всей числовой оси, поэтому найдем критические точки 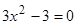. Отсюда находим, что 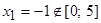и .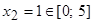

3. Вычислим значение функции в критических точках и на концах заданного отрезка: .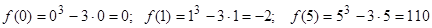

4. Из полученных чисел выбираем наименьшее 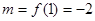и наибольшее 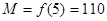, которые определяют наименьшее и наибольшее значения функции 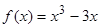на отрезке .

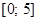3. Выпуклость вверх и вниз графика функции. Точки перегиба.

О1. График функции называется выпуклым вверх на интервале 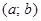, если он лежит ниже любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 81).

 

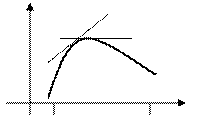
Рис. 81. Выпуклый вверх график функции .

 

 

О2. График функции называется выпуклым вниз на интервале 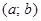, если он лежит выше любой касательной, проведенной к графику этой функции на заданном интервале (Рис. 82).

 

Рис. 82. Выпуклый вниз график функции .

 

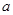
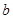
Достаточные условия выпуклости вверх и вниз графика функции на том или ином интервале определяются теоремой:

Т3. Если вторая производная функции на интервале 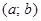существует и положительна, то на этом интервале график функции будет выпуклым вниз. Если вторая производная функции на интервале 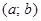существует и отрицательна, то на этом интервале график функции будет выпуклым вверх.

Пример 3. Определить направление выпуклости графика функции .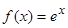

Найдем вторую производную от заданной функции 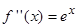. В силу того, что 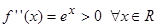, то график функции 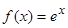будет выпуклым вниз на всей числовой оси.

Пример 4. Определить характер выпуклости графика функции .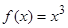

Найдем вторую производную от заданной функции 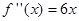. В силу того, что 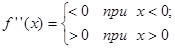, то график функции 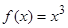будет выпуклым вверх при отрицательных значениях аргумента и выпуклым вниз при положительных значениях аргумента.

О3. Точка, отделяющая вогнутую часть графика функции от выпуклой (или выпуклую часть графика функции от вогнутой), называется точкой перегиба.

Выясним необходимые и достаточные условия существования точек перегиба.

4. Необходимое и достаточное условия существования точки перегиба.

Рассмотрим необходимое условие существования точки перегиба.

Т4. Если функция дважды непрерывно дифференцируема на не-котором интервале, содержащем точку перегиба 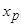, то в точке перегиба вторая производная равна нулю, т.е. .

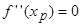З1. Обращение в нуль второй производной функции в точке перегиба является необходимым, но не достаточным условием существования та-кой точки на графике функции.

Пример 5. Доказать, что точка 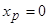не является точкой перегиба графика функции .

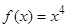Если вычислить вторую производную от заданной функции, то она будет равна 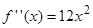. Если приравнять это выражение к нулю, то получим, что точка 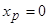должна быть точкой перегиба графика функции 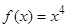. Однако график этой функции на всей числовой оси является вогнутым, т.е. точка 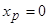не является точкой перегиба графика функции 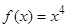. В связи с этим рассмотрим достаточное условие существования точки перегиба.

Т5. Пусть функция дважды непрерывно дифференцируема на некотором интервале, вторая производная которой в точке 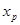, принадлежащей этому интервалу, обращается в нуль ( 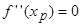) или не существует. Если при переходе через точку 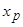вторая производная функции меняет свой знак, то точка 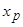определяет точку перегиба графика функции .

Пример 6. Найти точки перегиба и интервалы выпуклости и вогнутости гра-фика функции .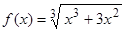

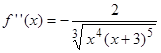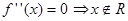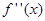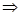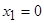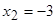Найдем втотрую производную заданной функции . Найдем точки подозрительные на перегиб: а) б) – не существует знаменатель дроби обращается в ноль при и . Отложим эти точки на числовой оси и определим знак второй производной на каждом интервале:

+ – –

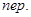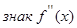
–3 0

 

Из рисунка видно, что точка 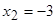является точкой перегиба, так как при переходе через нее вторая производная изменяет свой знак. Точка 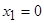не является точкой перегиба, так как при переходе через нее вторая производная не изменяет своего знака.

 

5. Асимптоты графика функции .

В большинстве практических случаев необходимо знать поведение функции при неограниченном росте (убыли) аргумента. Одним из наиболее интересных случаев, которые возникают при таком исследовании, является случай, когда график функции неограниченно приближается к некоторой прямой.

О4. Прямая ( 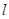): 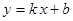называется асимптотой графика функции , если расстояние от переменной точки графика до этой прямой стремится к нулю при стремлении аргумента 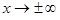, т.е. .

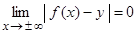З2. График функции может приближаться к асимптоте сверху, снизу, слева, справа или колеблясь возле этой прямой (Рис. 83).

 

 

 

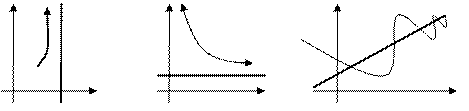
Рис. 83. Различные случаи приближения графика функции к асимптотам.

 

Различают вертикальные, горизонтальные и наклонные асимптоты.

О5. Вертикальная прямая 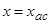называется вертикальной асимптотой, если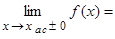 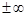. Горизонтальная прямая 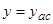называется горизонтальной асимптотой, если 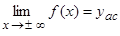. Прямая 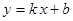называется наклонной асимптотой (параметр 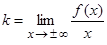и параметр 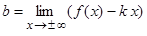отличаются от 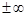и ).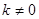

З3. Горизонтальная асимптота является частным случаем наклонной асимптоты: если 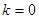, то наклонная асимптота вырождается в горизонтальную 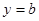, при условии, что 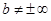. Если параметр 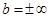, то горизонтальной асимптоты нет.

6. Полная схема исследования функции с помощью производных.

1. Находят область определения функции. При наличии точек разрыва II рода изучают поведение функции в их малой окрестности, т.е. вычисляют лево- и правосторонние пределы. При задании функции словесным образом также вычисляют лево- и правосторонние пределы для граничных точек интервалов, на которых функция описывается разными формулами.

⇐ Предыдущая123456Следующая ⇒

Поделиться: