
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
I. Вычислить определенные интегралы. ⇐ ПредыдущаяСтр 3 из 3
II. Вычислить определенные интегралы. Вариант 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
| 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
| 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
| 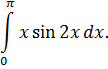
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
| 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 9
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 1 1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 12
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 13
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
| 
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 14
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 18
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 19 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 20
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 2 1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 22 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 24 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 25
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
III . Вычислить несобственные интегралы или доказать их расходимость.
Вариант 1
Вариант 2
Вариант 3












|
Вариант 4 |
Вариант 5 |
Вариант 6 | |||

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
|
Вариант 7 |
Вариант 8 |
Вариант 9 | |||

| 
| 
| 
| 
| 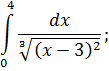
|

| 
| 
| 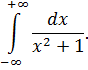
| 
| 
|
|
Вариант 10 |
Вариант 11 |
Вариант 12 | |||

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 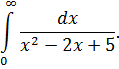
|
|
Вариант 13 |
Вариант 14 |
Вариант15 | |||

| 
| 
| 
| 
| 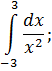
|

| 
| 
| 
| 
| 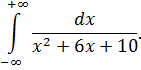
|
|
Вариант 16 |
Вариант 17 |
Вариант 18 | |||

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
|
Вариант 19 |
Вариант 20 |
Вариант 21 | |||

| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
|
|
Вариант 22 |
Вариант 23 |
Вариант 24 | ||||

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
|
| |
|
Вариант 25 | |

| 
|

| 
|
III. Вычислить площади фигур, ограниченных линиями.
IV.
| 1. | 
| 
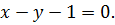
| 
| 
|
| 2. | 
| 

| 
| 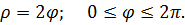
|
| 3. | 
| 

| 
| 
|
| 4. | 
| 

| 
| 
|
| 5. | 
| 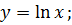

| 
| 
|
| 6. | 
| 
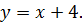
| 
| 
|
| 7. | 
| 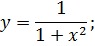
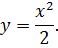
| 
| 
|
| 8. | 
| 
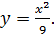 
| 
| 
|
| 9. | 
| 
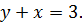
| 
| 
|
| 10. | 
| 
 
| 
| 
|
| 11. | 
| 
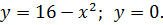
| 
| 
|
| 12. | 
| 

| 
| 
|
| 13. | 
| 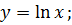

| 
| 
|
| 14. | 
| 

| 
| 
|
| 15. | 
| 
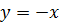
| 
| 
|
| 16. | 
| 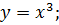

| 
| 
|
| 17. | 
| 

| 
| 
|
| 18. | 
| 

| 
| 
|
| 19. | 
| 

| 
| 
|
| 20. | 
| 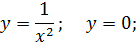

| 
| 
|
| 21. | 
|  
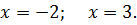
| 
| 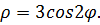
|
| 22. | 
| 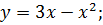

| 
| 
|
| 23. | 
| 
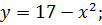

| 
| 
|
| 24. | 
| 


| 
| 
|
| 25. | 
| 

| 
| 
|
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №2
«Дифференциальные уравнения»
Вариант 0
I. Решить уравнение  .
.
II. Найти общее решение уравнения  .
.
III. Найти общее решение уравнения:
а) 
б) 
IV. Найти общее решение уравнения (без нахождения неопределенных коэффициентов).
а) 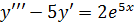
б) 
V. Решить задачу Коши.
 y (0) = 0 ; y ’ (0) = 0
y (0) = 0 ; y ’ (0) = 0
VI. Найти общее решение уравнения методом вариации произвольных постоянных.

Решение.
I. 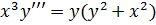
Разделим обе части уравнения на х3, получим

Правая часть этого уравнения есть функция отношения  ,
,
следовательно , это однородное уравнение.
Обозначим 
 и
и 
Имеем: 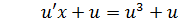
 - это уравнение с разделяющимися переменными
- это уравнение с разделяющимися переменными

Интегрируем:
 . Подставим
. Подставим 
Если константу С записать в другом виде «  », то общее решение будет иметь вид:
», то общее решение будет иметь вид:

В процессе решения мы делили обе части уравнения на х3≠0 и u3 ≠0 и могли потерять решения х=0 и u=0 ( u=0 
 =0
=0  y=0)
y=0)
Непосредственной проверкой убеждаемся , что х = 0 не является решением; а у = 0 – решение, которое не входит в общий интеграл ни при каком С
Имеем ответ:  ; у=0.
; у=0.
II. 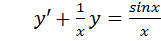
Это линейное уравнение 
Пусть 
Имеем 
 – уравнение с разделяющими переменными.
– уравнение с разделяющими переменными.
 ,
,
т.к 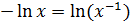
 , подставим найденное u
, подставим найденное u

Интегрируем 
Тогда 
Ответ: 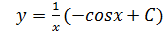
III. a) 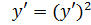
Это уравнение второго порядка, не содержащее функцию у.
Положим 
Уравнение имеет вид 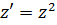 – это уравнение с разделяющимися переменными.
– это уравнение с разделяющимися переменными. 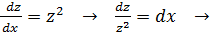
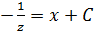 .
.
Вернемся к у , получаем

Это и будет ответом.
б) 
Это уравнение второго порядка, не содержащее Х.
Положим 
Имеем 
 p ( p ’
p ( p ’  2 y ) = 0
2 y ) = 0
1) p = 0 
 = 0
= 0  y = C
y = C
2) 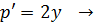




Ответ: y=C; 
IV. а) 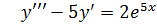
Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами.
1) Рассмотрим однородное уравнение: 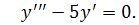
Составим характеристическое уравнение и найдем его корни
k3 - 5k = 0  k(k2-5) = 0
k(k2-5) = 0  k1 = 0 k2,3 = ±
k1 = 0 k2,3 = ± 
Следовательно , 

- oбщее решение однородного уравнения в случае действительных различных корней характеристического уравнения.
2) Правая часть неоднородного уравнения  ;
;  – многочлен нулевой степени,
– многочлен нулевой степени,  (α – не является корнем характеристического уравнения). Тогда
(α – не является корнем характеристического уравнения). Тогда  – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
3) Найдем неопределенный коэффициент А
Имеем 



Подставим найденные производные в исходное уравнение



 . Известно, что
. Известно, что 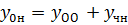
Ответ: 
б) Найти вид общего решения уравнения

1). Составим характеристическое уравнение и найдем его корни:

если корни характеристического уравнения комплексны α±β  , то
, то
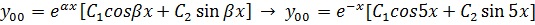
2). Правая часть уравнения имеет вид:
 , где
, где
 - многочлен степени 2
- многочлен степени 2
 - многочлен степени 1
- многочлен степени 1
Для правой части нашего уравнения
 ,
,
здесь  многочлен 2-ой степени c неопределенными коэффициентами.
многочлен 2-ой степени c неопределенными коэффициентами.
3) Общее решение неоднородного уравнения y0н есть сумма общего решения однородного уравнения y00 и частного решения неоднородного уравнения yчн y0н=y00+yчн
Имеем

V.  ;
;  ;
; 
1) Найдем y00 для уравнения 
Характеристическое уравнение k2 - 2k = 0  k1 = 0; k2 = 2
k1 = 0; k2 = 2
Корни действительны и различны, следовательно,

2) Найдем yчн ,  ;
;  – многочлен, α = 0.
– многочлен, α = 0.
Значит, 
Множитель Х появляется из-за того, что α = 0 есть однократный корень характеристического уравнения.
3) Найдем коэффициенты A, B, C
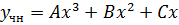


Подставим в уравнение 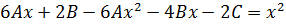
Отсюда:  →
→ 

4) Чтобы решить задачу Коши, нужно найти С1 и С2 , воспользовавшись начальными условиями:

Ответ:  – искомое решение.
– искомое решение.
VI. 
1) Рассмотрим однородное уравнение  и найдем корни его характеристического уравнения
и найдем корни его характеристического уравнения

т.е. функции  и
и  будут частными решениями этого однородного уравнения.
будут частными решениями этого однородного уравнения.
2) Запишем решение неоднородного уравнения в виде:
 и составим систему уравнений для нахождения
и составим систему уравнений для нахождения 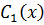 и
и 

Применим метод Крамера для решения системы:
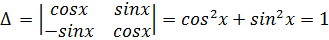


Тогда 

Ответ: 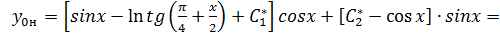
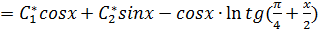
КОНТРОЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ №2
I. Найти общее решение уравнения:
1. 
2. 
3. 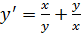
4. 
5. 
6. 
7. 
8. 
9. 
10. 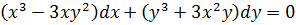
11. 
12. 
13. 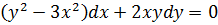
14. 
15. 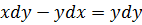
16. 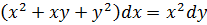
17. 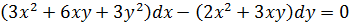
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 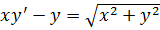
I. Найти общее решение уравнения:
1. 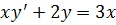
2. 
3. 
4. 
5. 
6. 
7. 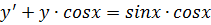
8. 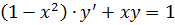
9. 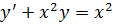
10. 
11. 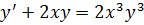
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 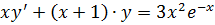
21. 
22. 
23. 
24. 
25. 
II. Найти общее решение уравнения:
1. а) 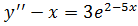 ;
;
б)  , y (0) = - 1 , y ’(0) = 1
, y (0) = - 1 , y ’(0) = 1
2. а) 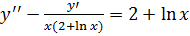 ;
;
б) 
3. а) 
б) 
4. а) 
б) 
5. а) 
б) 
6. а)  ;
;
б) 
7. а) 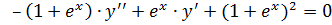 ;
;
б) 
8. а) 
б) 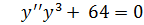 , y (0) = 4, y ’(0) = 2
, y (0) = 4, y ’(0) = 2
9. а) 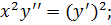
б) 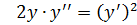
10. а)  ;
;
б) 
11. а) 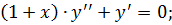
б) 
12. а) 
б) 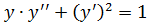
13. а) 
б) 
14. а) 
б) 
15. а) 
б) 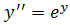
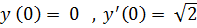
16. а) 
б) 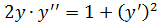
17. а) 
б) 

18. а) 
б) 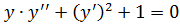
19. а)  ;
;
б) 
20. а)  ;
;
б) 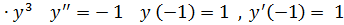
21. а)  ;
;
б) 
22. а)  ;
;
б) 
23. а)  ;
;
б) 
24. а) 
б)  +1
+1
25. а) 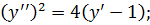
б) 
Последнее изменение этой страницы: 2019-03-22; Просмотров: 272; Нарушение авторского права страницы