Кинематическая схема лопастного движения жидкости. Составляющие скорость потока.

Кинематика жидкости устанавливает законы её движения, независимо от сил, действующих на жидкость.

Кинематика потока жидкости в лопастных гидравлических насосах изучает законы движения жидкости в полости лопастного колеса насоса, независимо от сил, действующих на жидкость со стороны лопастей.

Определение. Закруткой потока называется проекция вектора абсолютной скорости жидкости на направление вектора 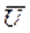её окружной скорости (рис.7).

Основу кинематики потока жидкости в рабочей полости лопастного колеса центробежного насоса составляет схема движения жидкости, изображённая на рис. 7.

Здесь показано, что жидкость, двигаясь в полости лопастного колеса центробежного насоса, участвует в двух движениях: перемещается вдоль лопасти с относительной скоростью и вращается с окружной (переносной) скоростью 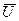вокруг оси вращения вала, то вектор абсолютной скорости частицы жидкости, равен векторной сумме двух её скоростей и согласно равенству:

;

Вектор направлен по касательной к лопасти в данной точке потока жидкости; вектор окружной скорости направлен перпендикулярно радиусу .

 

Рис. 7. Схема окружного и радиального сечений лопастного колеса насоса.

На рис. 5 вектор определяется проекцией вектора на направление вектора . Закрутка потока определяет напор насоса, который изменяется в соответствии с изменением закрутки. В зависимости от направления потока жидкости, от расхода жидкости , а также от оборотов вала насоса, закрутка потока , как и напор насоса, может быть положительной, отрицательной и равной нулю.

Легко видеть, что если закрутка потока перед входом на кромки лопастей насоса равна нулю , то напор насоса при постоянных оборотах вала насоса ( ) полностью определяется только закруткой потока на выходе из лопастного колеса согласно формуле:

(4)

Последнее равенство является основным в теории лопастных гидромашин.

Закрутка потока, равная нулю , может быть в случае, когда поток жидкости перед входом в лопастной центробежный насос не закручен каким–либо способом, например, когда перед входом в основной насос не установлен дополнительный осевой насос.

В кинематике центробежных лопастных гидронасосов есть еще одно важное понятие – вектор , который называют радиальной составляющей абсолютной скорости . Он определяет теоретическую подачу (расход) насоса.

Определение. Вектор соответствует проекции вектора на направление радиуса , проведенного в данную точку потока из точки О – центра вращения вала насоса.

На рис. 7 показано, что

Отсюда следует, что важнейшее равенство в теории лопастных гидромашин:

 

Радиальная составляющая абсолютной скорости определяет теоретическую подачу (расход) 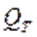насоса.

На рис. 7 видно, что

,

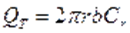Отсюда

Величина равна площади кольца длиной и шириной 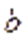. Параметр 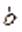–один из основных геометрических параметров лопастных гидромашин, он равен ширине лопасти в той точке, через которую проведено кольцевое сечение насоса. На рис. 7 это сечение обозначено окружностью, с радиусом r.

Таким образом, закрутка потока определяет теоретический (без потерь) напор насоса, а радиальная составляющая абсолютной скорости 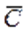определяет теоретическую (без потерь) подачу 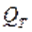насоса.

Из рис. 7 следует, что закрутка потока и радиальная скорость связаны равенством:

 

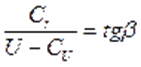
Здесь угол наклона касательной к лопасти в данной точке потока к направлению вектора и отсчитывается от вектора против часовой стрелки.

Отсюда

                                                                 

Таким образом, в случае, когда дополнительный осевой насос на входе в центробежный насос отсутствует, а такие случаи, в основном, и встречаются на практике, теоретический напор 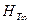центробежного насоса рассчитывается по

формуле:

( 5)

Или, с учётом того, что

,

.

Таким образом, напор насоса, полностью определяется геометрией его лопастей на выходе колеса, а также оборотами его вала и расходом жидкости, проходящей через насос.

Зависимость теоретического напора насоса от его подачи.

 

При постоянном числе n оборотов вала насоса все величины в правой части уравнения (5) за исключением , будут постоянными, поэтому можно ввести обозначение:

и ,

отсюда

(6)

Уравнение (6) устанавливает функциональную зависимость между теоретическим напором насоса и его теоретической производительностью .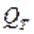

Соответствующая графическая зависимость показана на рис. 8.

Из равенства (6) следует, что графическая зависимость при постоянных оборотах 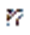вала насоса и угле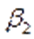 наклона лопасти ( ) – есть прямая наклонная линия.

Точка 1 на графике определяет холостой ход насоса. В этом случае кран за насосом закрыт. Подача насоса равна нулю . Теоретический напор насоса максимальный и равный . Закрутка потока будет в этом случае также максимальной и равной .

 

 

Рис.6. Теоретическая напорная характеристика лопастного центробежного насоса.

Точка 2 на графике соответствует нулевому напору =0. Подача Q в этом случае будет максимальной и равной

(7)

Этот факт, кажущийся на первый взгляд парадоксальным, поясняется следующим. При постоянных оборотах вала насоса окружная составляющая 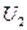абсолютной скорости потока остаётся постоянной

.

С увеличением подачи, т.е. расхода жидкости через насос, радиальная скорость также увеличивается, растёт и относительная скорость W. При этом угол также растёт, а закрутка 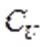потока, наоборот уменьшается и, наконец, становится равной нулю при подаче 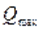, которая определяется равенством (7).

Физический смысл этого явления состоит в том, что с увеличением расхода жидкости через насос относительная скорость частиц жидкости настолько увеличивается, что лопасти насоса не успевают закрутить поток и , следовательно, никакой дополнительной энергии сообщить жидкости не могут. На практике такие явления в лопастных насосах не реализуются, так как при увеличении скорости обтекания лопастей насоса ( до 30 м/с), давление, согласно уравнению Д. Бернулли, настолько уменьшается, что на передних кромках лопастей насоса возникает холодное кипение жидкости, которое называют кавитацией. После дальнейшего увеличения скорости, наступает кавитационный срыв работы насоса (см. рис. ).

⇐ Предыдущая12345Следующая ⇒

Поделиться: