Синтез технической структуры АСУТП на основе конденсации графовой функциональной модели системы

(В.Я. Войтенко, А.В. Кузнецов «Приборы и системы управления», №4, 1991г.)

 

Рассмотрим синтез оптимальной по числу технических элементов структуры АСУТП для одного ее уровня, например, нижнего (локального) уровня иерархии АСУТП, с дальнейшим обобщением и применением полученных результатов для синтеза ее последующих уровней. Будем считать, что рассматривается структура технических средств АСУТП, включающая в качестве элементов технические устройства (например, контроллеры) и линии управления, контроля и сигнализации в качестве линий связи.

         Постановка задачи и ее математическая модель

Техническую структуру локального уровня АСУТП, на которую возлагается решение некоторого множества L предназначенных для автоматизированного выполнения задач (функций), определим отображением d множества L={ℓ _j}, j=1,.., k на множество M={m_i}, i=1,.., n технических документов (процессоров) АСУ, которые необходимо использовать для построения технической структуры (ТС) локального уровня АСУТП, т.е.

 d: L → M → {ℓ _j} → {m_i}                                                         (1)

при условии экстремума некоторого критерия оптимальности Q_опт ТС АСУТП, характеризующего степень рациональности выбора числа n технических элементов АСУТП с учетом связности задач системы и удовлетворения следующих ограничений:

1. однородность элементов ТС АСУТП и равнозначности связей между задачами одного уровня;

2. согласованности величин информационной емкости I_j задач ℓ _j локального уровня управления с допустимыми объемами памяти V_j^* устройств ЭВТ, реализующих технические элементы АСУТП; при этом из-за предыдущего ограничения справедливо равенство  V₁^*=V₂^*=^…=V_n^*=V^*;

3. не превышения времени t_j решения (обработки) задач ℓ _j некоторых пороговых (допустимых) значений T_i^*, определяемых динамикой технологического процесса (ТП);

4. замкнутости (разомкнутости) межэлементного шинного интерфейса ТС АСУТП одного уровня.

С учетом сделанных ограничений синтез оптимальной ТС АСУТП сводится к определению требуемого оптимального числа n однородных технических элементов АСУТП, необходимых для решения задач локального уровня АСУТП, и распределению связей между этими элементами. Другими словами, нужно определить минимальное число, а также состав и взаимосвязи подмножеств сильно связанных задач, каждое из которых решается своим техническим элементом m_i; при этом число задач, входящих в состав таких подмножеств, может принимать значения от 1 (тогда число подмножеств равно k) до k (число подмножеств равно 1), а значит, и число n требуемых для их решения технических элементов согласно выражению (1) может варьироваться от k до 1.

Сильно связными будем полагать взаимно связные, а слабо связными – односторонне связные задачи рассматриваемого уровня иерархии ТС АСУТП.

Формализацию поставленной задачи проведем на базе математического аппарата теории графов.В этом случае она может быть сформулирована следующим образом:

найти минимальное значение величины n, равное минимальному числу сильно связных компонент графа G_i; i=1,..n, информационного графа G:

G=(‹L, V, T›, ‹F, W›), где

L={ℓ _j}, j=1,.., k – множество автоматизируемых задач АСУТП локального уровня, соответствующих вершинам графа G;

V={v_j}, j=1,.., k – множество, каждый элемент которого определяет требуемый в процессе решения j-й задачи объем памяти, непосредственно зависящий от значения информационной емкости I_j задачи ℓ _j, т.е. v_j=f(I_j);

T={t_j}, j=1,..k – множество, каждый элемент которого определяет время, требуемое для решения j-й задачи;

F={f_js}, j=1,.., k; s=1,.., k – множество связей (дуг графа G) между задачами, причем равенство индексов j=s допустимо, что соответствует связи каждой вершины графа G с самой собой посредством дуги, называемой петлей, изображение которой на графе, как правило, опускается с целью упростить его схему;

W={w_js}, j=1,..k; s=1,.., k – множество весов соответствующих дуг графа G, соединяющих его вершины; вследствие ограничения, сформулированного в п. 1) каждый элемент w_js множества W положим равным 1 (w_js=1),

причем таких сильных компонент, что

: G_i≠ 0, G_i∩ G_u=0, i, u=1,.., n; u≠ i =G

и обеспечивается условие:

Q_опт → max

при ограничениях

(объем памяти процессора)                                 (2)

(время решения всех задач i-ым процессором) (3)

Рассмотрим на примере решение сформулированной задачи определения минимального числа, а также состава и взаимосвязей подмножеств сильно связных задач управления, контроля и сигнализации локального уровня АСУТП, каждое из которых будет решаться своим техническим элементом m_i.

f24

f15

f51

f21

f65

f43

f36

f64

G2 ~ m2

G3 ~ m3

ℓ 2

ℓ 5

ℓ 6

ℓ 1

ℓ 3

f31

G1 ~ m1

ℓ 1

v1 t1

v5 t5

v2 t2

v3 t3

v6 t6

v4 t4

Пусть в результате функционального анализа объекта управления (ТП) установлено множество L={ℓ _j}, j=1,.., k задач, решение которых подлежит автоматизации. Описаны также все условные и безусловные, непосредственные и косвенные, прямые, обратные и взаимные, а также другие связи между ними, на основе чего выстраивается информационный граф G, вершинами которого являются сами задачи ℓ _j и их атрибуты (v_j, t_j), а ориентированными дугами – связи f_js между задачами. На рис. 4.6.1.  дан пример такого графа G.

 

Рис. 4.6.1. Пример графа G

Алгоритм решения задачи

 

Поставленная задача решается на основе реализации процедуры конденсации G^* графа G путем отыскания его сильных компонент, число которых априорно неизвестно.

Граф G^* называемый конденсацией графа G, определяется следующим образом: каждая его вершина m_i соответствует множеству вершин некоторой сильной компоненты G_i графа G, т.е. m_i~G_i= (разным сильным компонентам из графа G отвечают разные вершины в конденсации G^*); дуга f_iu^* существует в конденсации G^* тогда, когда в графе G имеется такая дуга f_js, что вершина ℓ _j принадлежит сильной компоненте графа G_i, соответствующей вершине m_i в конденсации G^*, а вершина ℓ _s – сильной компоненте графа G_u, отвечающей вершине m_u в конденсации G^*, т.е.

~ ~

Сильными компонентами графа G_i будем считать максимальные подграфы графа G, обладающие заданным свойством. Поскольку в данном случае в качестве такого свойства выступает сильная связность вершин графа G, его сильные компоненты будут представлять собой подмножества (порожденные подграфы) взаимно связных вершин.

Требуется найти его сильные компоненты и построить конденсацию G^*.

Эта процедура реализуется при использовании матриц достижимости R_G и контрдостижимости Q_G графа G.

Матрица достижимости R_G=||r_js|| определяется следующим образом:

 

 

      1, если вершина ℓ _s достижима из вершины ℓ _j (т.е. ℓ _j→ ℓ _s)

r_js=

      0, в противном случае, т.е. ℓ _j → ℓ _s.

 

Вершина ℓ _s считается достижимой из вершины ℓ _j, если существует путь от вершины ℓ _j

к вершине ℓ _s.

Все диагональные элементы матрицы R_G равны 1, т.к. каждая вершина достижима из самой себя путем длиной 0. В качестве алгоритма построения матрицы достижимости R_G можно предложить следующий:

Вход: Матрица A_G смежности графа G, состоящая из строк A₁, A₂, …, A_j, …, A_k; A_j=(a_j1, …, a_js, …, a_jk)

Выход: Матрица достижимости R_G, состоящая из строк R₁, R₂,..., R_j, …, R_k, где

 

R_j=(r_j1, …, r_js, …, r_jk)

 

Алгоритм запишем в виде, использующем псевдоалгол:

Начало

1. для j от 1 до k шаг 1 цикл А

2. сформировать множество S индексов s таких, что a_js=1;

3. R_j: = A_j ; k: =0;

4. пока S≠ 0 цикл В

5. выбрать sєS;

6. R_j: =R_j A_s;

7. S: =S\{s};

8. K: =K {s};

9. Сформировать множество S_s индексов r таких, что a_sr=1;

10. S: =S (S_s\K);

11. конец цикла В;

12. возврат R_j;

13. конец цикла А;

Конец

 

Для примера матрица смежности A_G имеет вид:

 

		ℓ 1	ℓ 2	ℓ 3	ℓ 4	ℓ 5	ℓ 6
	ℓ 1	0	0	0	0	1	0
	ℓ 2	1	0	0	1	0	0
AG= ℓ 3		1	0	0	0	0	1
	ℓ 4	0	0	1	0	0	0
	ℓ 5	1	0	0	0	0	0
	ℓ 6	0	0	0	1	1	0

 

Применяя описанный выше алгоритм, получаем следующую матрицу достижимости R_G:

 

		ℓ 1	ℓ 2	ℓ 3	ℓ 4	ℓ 5	ℓ 6
	ℓ 1	1	0	0	0	1	0
	ℓ 2	1	1	1	1	1	1
RG= ℓ 3		1	0	1	1	1	1
	ℓ 4	1	0	1	1	1	1
	ℓ 5	1	0	0	0	1	0
	ℓ 6	1	0	1	1	1	1

 

Матрица контрдостижимости Q_G=║ q_js║ определяется следующим образом:

      1, если из вершины ℓ _s графа G достижима вершина ℓ _j (т.е. ℓ _j← ℓ _s)

q_js=

      0, в противном случае, т.е. ℓ _j ← ℓ _s.

При этом q_js=1, если j=s.

Очевидно, что матрица Q_G есть транспонированная матрица R_G.

Для нашего примера имеем:

 

		ℓ 1	ℓ 2	ℓ 3	ℓ 4	ℓ 5	ℓ 6
	ℓ 1	1	1	1	1	1	1
	ℓ 2	0	1	0	0	0	0
QG= ℓ 3		0	1	1	1	0	1
	ℓ 4	0	1	1	1	0	1
	ℓ 5	1	1	1	1	1	1
	ℓ 6	0	1	1	1	0	1

 

На следующем этапе алгоритма выполняется поэлементное умножение матриц R_G и Q_G графа G, в результате чего получаем R_G Q_G:

		ℓ 1	ℓ 2	ℓ 3	ℓ 4	ℓ 5	ℓ 6
	ℓ 1	1	0	0	0	1	0
	ℓ 2	0	1	0	0	0	0
RG  QG= ℓ 3		0	0	1	1	0	1
	ℓ 4	0	0	1	1	0	1
	ℓ 5	1	0	0	0	1	0
	ℓ 6	0	0	1	1	0	1

 

При этом строка ℓ _j матрицы R_G  Q_G содержит единицы только в тех столбцах ℓ _s, для которых выполняется условие: вершины ℓ _j и ℓ _s взаимно достижимы. В других местах строки стоят нули. Таким образом, две вершины графа G находятся в одной и той же сильной компоненте тогда, когда соответствующие им строки (или столбцы) в матрице R_G  Q_G идентичны.

Следующий шаг алгоритма – преобразование матрицы R_G  Q_G путем транспонирования ее строк и столбцов в блочно-диагональную матрицу (R_G  Q_G)^′ , каждая из диагональных подматриц (блоков) которой соответствует сильной компоненте графа G и содержит только единичные элементы, поскольку вершины, которым отвечают строки, имеющие единицу в столбце ℓ _s, образуют множество вершин сильной компоненты, содержащей вершину ℓ _s. Все остальные блоки данной матрицы имеют нули. Для нашего примера имеем:

 

		ℓ 1	ℓ 5	ℓ 2	ℓ 3	ℓ 4	ℓ 6
	ℓ 1	1	1	0	0	0	0
	ℓ 5	1	1	0	0	0	0
(RG  QG)′ = ℓ 2		0	0	1	0	0	0
	ℓ 3	0	0	0	1	1	1
	ℓ 4	0	0	0	1	1	1
	ℓ 6	0	0	0	1	1	1

 

Анализ матрицы (R_G  Q_G)^′ позволяет получить число n и состав подмножеств сильно связных задач локального уровня АСУТП, решаемых каждое своим m_i-м техническим элементом i=1,.., n. В данном примере в состав G входит три сильные компоненты, следовательно, число однородных технических элементов, которые могут быть использованы для построения оптимальной ТС локального уровня АСУТП, равно 3, т.е. имеем:

=G

U

l

1

5

1

l

                     ~

 

~

 

~

 

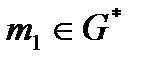
На основе блочно-диагональной матрицы (R_G  Q_G)^′ , а также структуры самого информационного графа G (см. рис. 4.6.2) строится его конденсация – граф G^*, определяющий связи между m_i-ми техническими элементами ТС АСУТП на локальном уровне, i=1, 2, 3 (см. рис. 3.16).

m1

m3

m2

Рис. 4.6. 2.  Конденсация G^* графа G

 

В соответствии с определением конденсации графа и его сильных компонент, а также с учетом принятых ограничений (2) и (8) для элементов графа G^* справедливы соотношения:

где i=1, 2, 3 для рассмотренного примера.

Кроме того, имеют место соответствия:

f₂₁^*~f₂₁; f₂₃^*~f₂₄; f₃₁^*~f₃₁

Таким образом, для построения оптимальной по числу элементов n ТС АСУТП определены все ее составные части: число n технических элементов, состав подмножеств сильно связных задач, решаемых каждым из них, а также взаимосвязи между элементами ТС локального уровня АСУТП.

Если в ограничении, сформулированном в п. 4, задана замкнутость межэлементного шинного интерфейса данного уровня ТС АСУТП, то на основании результатов анализа блочно-диагональной матрицы (R_G  Q_G)^′ , а также полученных в конденсации G^* (см. рис. 2) связей f_iu^* (ориентированных дугах графа G^*)

 Выстраивается искомая децентрализованная ТС АСУТП в целом с единственным (локальным, первым, нижним) уровнем иерархии (см. рис. 4.6.3).

 

m1

m2

m3

ℓ 1

ℓ 2

ℓ 3

ℓ 4

ℓ 5

ℓ 6

Рис. 4.6.3. Децентрализованная одноуровневая оптимальная ТС АСУТП

Если в ограничении на ТС АСУТП определена разомкнутость соответствующего интерфейса или требуется построение многоуровневой иерархической ТС АСУТП, то, с учетом связей f_iu^*, составляется информационный граф G⁽²⁾ задач второго уровня ТС. Этот граф выстраивается по результатам функционального анализа множества задач (функций) этого уровня, лежащих в плоскости среза локального уровня, но решаемых соответственно на втором уровне иерархии ТС АСУТП. После этого относительно данного уровня ТС повторяется вся ранее описанная процедура синтеза. Аналогично выстраивается и все последующие уровни иерархической структуры АСУТП.

Физический эффект оптимизации обусловлен следующим:

 во-первых, сокращением числа связей между задачами каждого уровня ТС (на основе их внутреннего представления в соответствующих технических элементах), требующих взаимодействия различных элементов одного уровня, что увеличивает оперативность обмена информацией при соблюдении ограничений, определяемых выражениями (2) и (3),

 во-вторых, распараллеливанием решения только слабо связных задач фиксированного уровня ТС АСУТП.

При этом сильно связные задачи, образующие свою сильную компоненту в информационном графе задач соответствующего уровня, предлагается решать последовательно на одном своем техническом элементе, т.е. задачи разных сильных компонент решаются параллельно, а в составе одной сильной компоненты – последовательно.

При этом следует иметь в виду следующее:

- если каждая задача решается своим техническим элементом, то это дает возможность параллельной обработки всех задач одного уровня ТС, что приводит к увеличению оперативности обработки. Однако при этом возможна задержка при организации обмена между элементами, т.е. имеют место их простаивания в ожидании исходной информации. Кроме того, усложняются протоколы обмена, системные алгоритмы, модели и программы управления системой, заметно поднимается и стоимость такой системы.

- если все задачи решаются одним элементом (одномашинная или однопроцессорная вычислительная система), то здесь имеется возможность внутреннего представления всех связей между задачами, что устраняет задержки обмена и простаивания технических элементов, ожидающих в качестве исходных данных для решения своей задачи, результатов решения других задач на других элементах. Однако здесь возможно появление задержки из-за образующихся очередей задач на обслуживание, т.к. нет возможности для их параллельной обработки.

Приведенные доводы свидетельствуют в пользу предлагаемого метода синтеза оптимальной ТС АСУТП, свободного от перечисленных недостатков.

 

 

Лекция 1

 

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться: