Расходомеры постоянного перепада давления

К приборам постоянного перепада давления относятся ротаметры, поплавковые и поршневые расходомеры. Наибольшее применение имеют ротаметры и поплавковые расходомеры, шкалы которых практически равномерны. Их можно использовать для измерения малых расходов; потери давления в них незначительны и не зависят от расхода. Ротаметры и поплавковые расходомеры имеют большой диапазон измерения ^.

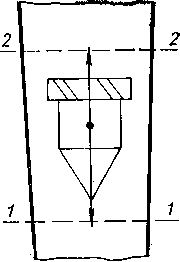
Поток жидкости или газа, проходящий через ротаметр (рис. 2.16) снизу, поднимает поплавок до тех пор, пока расширяющаяся кольцевая щель между телом поплавка и стенками конусной трубки не достигнет такой величины, при которой действующие на поплавок силы уравновешиваются. При равновесии сил поплавок устанавливается на некоторой высоте, зависящей от расхода.

На поплавок ротаметра сверху вниз действуют две силы: сила тяжести  и сила от давления потока на верхнюю плоскость поплавка f₁. Сила тяжести , где V – объем поплавка;  – плотность материала поплавка; g – ускорение свободного падения. Сила от давления потока на верхнюю плоскость поплавка равна f₁ = 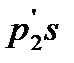, где  – среднее давление потока на единицу площади верхней поверхности поплавка; 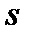 – площадь наибольшего поперечного сечения поплавка.

Снизу вверх на поплавок действуют также две силы: сила от давления потока на нижнюю плоскость поплавка f₂ = 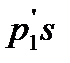 и сила трения потоков о поплавок  f _тр = , где k – коэффициент сопротивления, зависящий от числа Рейнольдса и степени шероховатости поверхности;  – средняя скорость потока в кольцевом канале, охватывающем боковую поверхность по­плавка; 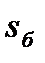 – площадь боковой поверхности поплавка;  – по-      казатель, зависящий от скорости.

Рис. 2.16

 

             Поплавок уравновешен в случае, если соблюдается равенство действующих сил:      

G _п + f ₁ = f ₂ + f _тр;

 

                            ,          

или

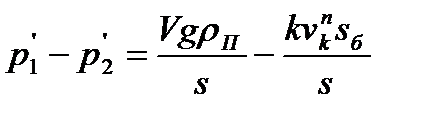                       (2.4)

 

Если допустить, что у_к при всех расходах – величина постоянная (с увеличением расхода увеличивается площадь кольцевого канала), то правая часть уравнения (2.4) будет постоянной, так как остальные величины для данного прибора неизменны. Следовательно, разность давлений на поплавок 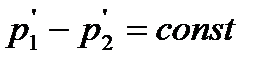, то есть ротаметр является расходомером постоянного перепада давления.

Разность статических давлений  изменяется, так как действует сила от динамического давления потока:

^,

где  – коэффициент сопротивления поплавка, зависящий от его формы;  – средняя скорость потока в сечении 1 – 1;  – плотность вещества, протекающего через ротаметр.

С увеличением расхода возрастает скорость , а, следовательно, и величина F; тогда разность статических давлений  должна уменьшаться (гидростатическое давление на поплавок, то есть архимедова сила, уже учтено в разности статических давлений ^,  действующих на поплавок).

 

Уравнение Бернулли для сечений 1 – 1 и 2 – 2

                        (2.5)

где  – среднее статическое давление в сечении 1 – 1, начиная с которого сказывается возмущающее воздействие поплавка на поток;  – среднее статическое давление в сечении 2 – 2, совпадающем с самым узким местом струи после прохода ее через коль­цевое отверстие;  – средние скорости потока в сечениях 1 – 1 и 2 –2; 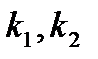 – коэффициенты неравномерности распределения скорости в сечениях 1 – 1 и 2–2;  – высота сечений 1–1 и 2–2 над некоторым начальным уровнем;  – коэффициент потерь энергии на участке между сечениями 1 – 1 и 2—2.

 Согласно условию неразрывности струи для сечений 1 – 1 и 2—2 справедливо равенство

                                 (2.6)

где Q – объемный расход жидкости;  – площади сечения потока в сечениях

1 – 1 и 2 – 2;  – коэффициент сужения струи;  – площадь кольцевого отверстия, образованного конусной трубкой и верхней частью поплавка.

Совместным решением уравнений (2.5) и (2.6) получим уравнение расхода

,             (2.7)

где  – коэффициент расхода;  – разность статических давлений, действующих на поплавок:

;

.

Если учесть динамическое давление потока на поплавок, то разность статических давлений

 .                           (2.8)

 

Подставив в уравнение (2.7) разность р₁ – р₂ из уравнения (2.8), получим:

 

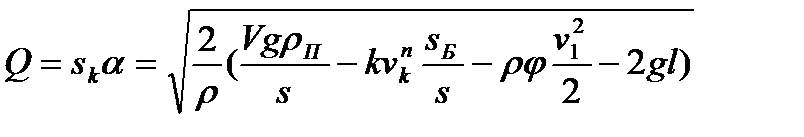.          (2.9)

 

 

Уравнение (2.9) можно представить в виде

 

,                       (2.10)

 

где .

Так как величины под корнем в уравнении (2.10) практически постоянны, то их можно заменить коэффициентом . Тогда уравнение ротаметра

 

                                               (2.11)

 Эта зависимость линейна, поэтому шкала ротаметра равномерная. Уравнения расхода (2.9), (2.11) получены для несжимаемой жидкости, для которой . При измерении расхода газа следовало бы в уравнение расхода ввести поправочный коэффициент к. Однако если учесть, что в ротаметрах перепады давлений не превышают 0, 005 МПа, то можно считать = 1.

Коэффициент расхода  для ротаметров зависит от большого числа величин, которые, как правило, не поддаются аналитическому определению, поэтому ротаметры градуируют экспериментально. Для экспериментальной градуировки ротаметров, предназначенных для измерения расхода жидкостей или газов, применяют в качестве градуировочной среды воду или воздух. Экспериментальная градуировка шкалы ротаметра точна лишь в том случае, если при эксплуатации значения всех величин, входящих в уравнение расхода, соответствуют градуировочным условиям. Изменение температуры потока меняет плотность среды и ее вязкость, а, следовательно, и коэффициент расхода. В еще большей степени будут изменяться величины, входящие в уравнение расхода, в случае, если ротаметр применяют для измерения расхода среды, отличающейся от градуировочной. В обоих случаях показания прибора необходимо умножать на поправочный коэффициент

,                            (2.12)

где  – коэффициент расхода и плотность среды, соответствующие градуировочным данным;  – действительные коэффициент расхода и плотность контролируемой среды.

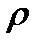Однако использовать формулу (2.12) практически невозможно, так как неизвестно значение коэффициента расхода . Только в случаях, когда вязкость среды очень мала и коэффициент расхода  незначительно меняется с изменением температуры и да­вления, можно использовать поправочный коэффициент в форме . Для газов, у которых  пренебрежимо мало по сравнению с 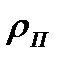, формула принимает вид .

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: