|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
|
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Журнал для лабораторных работ по гидравликеСтр 1 из 10Следующая ⇒
Журнал для лабораторных работ по гидравлике ( специальность ЗТ и МАЭС) Студент: Группа РАБОТА 1. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ СВОЙСТВ ЖИДКОСТИ Цель работы. Освоение техники измерения плотности, теплового расширения, вязкости и поверхностного натяжения жидкостей. Общие сведения Жидкость есть физическое тело, обладающее свойством текучести, т.е. свойством менять свою форму под действием малых сил. Основными свойствами жидкости, существенными при рассмотрении задач гидравлики, являются: плотность, сжимаемость, температурное расширение, вязкость и поверхностное натяжение. Свойства жидкости обуславливаются её молекулярным строением. Плотностью жидкости ρ называется её масса M, заключенная в единице объёма W: ρ = В практических приложениях о массе жидкости судят по её весу. Вес жидкости G, приходящийся на единицу объёма, называется удельным весом γ: γ = Плотность и удельный вес связаны между собой соотношением: γ = ρ g, где: g – ускорение силы тяжести. Плотность и удельный вес жидкостей меняются с изменением давления и температуры. Сжимаемость (свойство жидкости изменять свою плотность при изменении давления) характеризуется коэффициентом объёмного сжатия β w, который связывает относительное изменение объёма жидкости ∆ W/W с интенсивностью равномерного всестороннего сжатия ∆ p данного объёма жидкости: β W = – Температурное расширение (свойство жидкости изменять свой объём, а следовательно и плотность, при изменении температуры) характеризуется коэффициентом температурного расширения β t, который связывает относительное увеличение объёма жидкости ∆ W/W при повышении температуры ∆ T на 1К: β T = Свойство жидкости оказывать сопротивление усилиям сдвига характеризуется динамической и кинематической вязкостью. Динамическая вязкость μ, представляет собой отношение напряжения сдвига τ к градиенту скорости dV/dn (изменению скорости на единицу длины нормали к направлению
Кинематическая вязкость ν, представляет собой отношение динамической вязкости μ к плотности жидкости ρ: ν = μ /ρ. Динамическая и кинематическая вязкости зависят от рода жидкости и параметров состояния среды. При этом динамическая вязкость жидкости зависит только от температуры (с повышением температуры вязкость капельных жидкостей понижается), а кинематическая вязкость зависит как от температуры, так и от давления. Поверхностное натяжение – свойство жидкости образовать поверхностный слой взаимно притягивающихся молекул – характеризующихся коэффициентом поверхностного натяжения
Таблица 1.1
Описание устройства №1 Устройство для изучения физических свойств жидкости содержит 5 приборов, выполненных в общем прозрачном корпусе (рис. 1.1), на котором указаны параметры для обработки опытных данных. Приборы 3-5 начинают действовать при перевертывании устройства № 1. Термометр 1 показывает температуру окружающей среды и, следовательно, температуру жидкостей во всех устройствах.
Рис. 1.1. Схема устройства №1: 1 - термометр; 2 - ареометр; 3 - вискозиметр Стокса; 4 - капиллярный вискозиметр; 5 – сталагмометр.
Порядок выполнения работы
1.3.1. Определение коэффициента теплового расширения жидкости Термометр 1 имеет стеклянный баллон с капилляром, заполненные термометрической жидкостью, и шкалу. Принцип его действия основан на тепловом расширении жидкостей. Варьирование температуры окружающей среды приводит к соответствующему изменению объема термометрической жидкости и ее уровня в капилляре. Уровень указывает на шкале значение температуры. Коэффициент теплового расширения термометрической жидкости определяется в следующем порядке на основе мысленного эксперимента, т.е. предполагается, что температура окружающей среды повысилась от нижнего (нулевого) до верхнего предельных значений термометра и уровень жидкости в капилляре возрос па величину Подсчитать общее число градусных делений Вычислить приращение объема термометрической жидкости С учетом начального (при 0 °С) объема термометрии ческой жидкости W найти значение коэффициента теплового ческой жидкости W найти значение коэффициента теплового расширения Таблица 1.2
Общие сведения Для двух произвольно выбранных живых сечений I-I и II-II струйки реальной жидкости (рисунок 2.1) при установившемся движении уравнение Д. Бернулли имеет вид:
Слагаемые, входящие в уравнение (3.1), можно истолковать с геометрической и энергетической точек зрения. С геометрической точки зрения, слагаемые уравнения (3.1) являются высотами (напорами): z - геометрическая высота (напор), т.е. превышение центра тяжести рассматриваемого поперечного сечения струйки над плоскостью сравнения 0-0, выбираемой произвольно (рисунок 3.1); p/rg - пьезометрическая высота, т.е. высота подъема жидкости в пьезометре, подключенном к центру тяжести рассматриваемого сечения струйки, отвечающая гидродинамическому давлению р в этой точке; u2/2g - скоростная высота (напор), отвечающая местной скорости u,
С энергетической точки зрения, слагаемые уравнения (3.1) представляют собой разновидности удельной энергии, а именно: z - удельная потенциальная энергия положения жидкости в рассматриваемом сечении струйки; P/rg - удельная потенциальная энергия давления; u2/2g - удельная кинетическая энергия;
h`w1-2 - потеря полной удельной энергии струйки, т.е. часть ее, затраченная на преодоление работы сил внутреннего трения, обусловленного вязкостью жидкости. Удельной энергией называется энергия, приходящаяся на единицу веса жидкости. Величины слагаемых уравнения (2.1) могут быть определены опытным путем следующим образом: z - геометрическим нивелированием или же измерением линейкой; p/rg - с помощью пьезометрической трубки (пьезометра); u2/2g - по разности отметок уровней жидкости в скоростной и пьезометрической трубках, подключенных к рассматриваемой точке живого сечения струйки (рисунок 2.2); h`w1-2 - по разности отметок уровней воды в скоростных трубках, подключенных к сечениям I-I и II-II (рисунок 3.2).
Рисунок 3.1 – Диаграмма уравнения Д.Бернулли для струйки реальной жидкости
Рисунок 3.2 – Измерение скоростного напора u2/2g: а - напорное движение жидкости; б - безнапорное движение жидкости
Скоростная трубка (рисунок 2.2) представляет собой трубку, верхний конец которой открыт в атмосферу, а нижний изогнут навстречу скорости и в рассматриваемой точке потока жидкости. Благодаря этому у входа в изогнутый конец скоростной трубки кинетическая энергия частицы жидкости преобразуется в потенциальную энергию давления столба жидкости высотой hu= u2/2g. Поскольку срез нижнего конца скоростной трубки перпендикулярен вектору скорости, а срез нижнего конца пьезометра параллелен (рисунок 3.2), уровень жидкости в скоростной трубке всегда устанавливается выше, чем в пьезометре, на величину u2/2g. Прибор, объединяющий конструктивно пьезометрическую (П) и скоростную (С) трубки, называется трубкой Пито и широко применяется для измерения скорости движения жидкости Для двух сечений потока реальной жидкости уравнение Д. Бернулли имеет вид:
где hw1-2 - потеря полного напора (полной удельной энергии) на преодоление работы сил внутреннего и внешнего трения на пути между живыми сечениями потока жидкости I-I и II-II; a - коэффициент Кориолиса (корректив кинетической энергии), учитывающий неравномерность распределения местных скоростей Величина a зависит от режима течения жидкости, а также от вида движения. Так, при равномерном движении для ламинарного режима a=2, 0, а для турбулентного - a=1, 05…1, 15. Слагаемые уравнений (3.1) и (3.2) в различных живых сечениях можно изображать графически в виде диаграммы уравнения Д. Бернулли (графика напоров), рисунок 3.1, дающей наглядное представление о перераспределении по пути движения жидкости потенциальной и кинетической энергии, а также о характере убывания полной энергии. Описание установки Установка (рисунок 3.3) представляет собой трубопровод 2 переменного сечения с напорным баком 1, вода в который подается по питающему трубопроводу 8. Бак 1 снабжен переливным устройством 10 для поддержания уровня воды на постоянной отметке, чтобы обеспечить в трубопроводе 2 установившееся движение жидкости. К сечениям I-I…II-II трубопровода 2 подключены пьезометры 3 и скоростные трубки 4 для измерения величин p/rg и u2/2g. Расход воды в трубопроводе 2 регулируется вентилем 6. Для измерения расхода воды имеются мерный бак 7 и секундомер 5.
Рисунок 3.3 – Схема установки: 1 – напорный питающий бак; 2 – трубопровод переменного сечения; 3 – пьезометры; 4 – скоростные трубки; 5 – секундомер; 6 – вентиль для регулирования расхода воды; 7 – мерный бак; 8 – питающий трубопровод; 9 – переливное устройство Ед. Изм. |
Результаты измерений И вычислений | |||||||||||||||||||||||||||||||||||||||||||||
| I-I | II-II | III - III | ||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||||||||||||||||||||||||||||
| 1 | Геометрические высоты центров тяжести сечений z | м | ||||||||||||||||||||||||||||||||||||||||||||
| 2 | Отметки уровней воды в пьезометрах, т.е. гидростатические напоры (z+p/rg) | м | ||||||||||||||||||||||||||||||||||||||||||||
| 3 | Отметки уровней воды в скоростных трубках, т.е. полные напоры H=z + p/rg + u2/2g | м | ||||||||||||||||||||||||||||||||||||||||||||
| 4 | Пьезометрические высоты (z + p/rg ) –z | м | ||||||||||||||||||||||||||||||||||||||||||||
| 5 | Скоростные высоты u2/2g=H-(z + p/rg) | м | ||||||||||||||||||||||||||||||||||||||||||||
| 6 | Потери полного напора на пути между соседними живыми сечениями струйками h`wi-(i+1)=Hi – Hi+1 | м | ||||||||||||||||||||||||||||||||||||||||||||
| 7 | Суммарные потери полного напора h`wI-III=HI - HIII | м | ||||||||||||||||||||||||||||||||||||||||||||
| 8 | Объем воды в мерном баке W | м3 | ||||||||||||||||||||||||||||||||||||||||||||
| 9 | Продолжительность наполнения объема W в мерном баке t | с | ||||||||||||||||||||||||||||||||||||||||||||
| 10 | Расход воды в трубопроводе Q=W/t | м3/c | ||||||||||||||||||||||||||||||||||||||||||||
| 11 | Средняя скорость движения воды в v= Q/w | м/с | ||||||||||||||||||||||||||||||||||||||||||||
| 12 | Скоростная высота, отвечающая средней скорости v2/2g | м | ||||||||||||||||||||||||||||||||||||||||||||
| 13 | Разность скоростных высот (u2/2g – v2/2g) | м | ||||||||||||||||||||||||||||||||||||||||||||
|
Примечания 1 Для сечения III-III (см графу 6) числовые значения величин (позиции 5 и 8…12) те же, что и для сечения I-I 2 Потери полного напора h`w (позицию 6) между сечениями II-II и III-III принять равными потерям напора между сечениями I-I и II-II 3 Остальные величины для сеч. III-III (см. позиции 1…4) следует определить с привлечением уравнения Д. Бернулли (уравнение 2.1) | ||||||||||||||||||||||||||||||||||||||||||||||
3.4 Контрольные вопросы
1. Объясните, чем обусловлены потери полного напора и каков их энергетический смысл?
2. Поясните, что понимают под термином " удельная энергия"?
3. Объясните термины " местная скорость" и " средняя скорость" и укажите, как определяют эти скорости?
4. Поясните, что такое линия полного напора и пьезометрическая линия, что будут представлять собой эти линии при равномерном движении реальной жидкости?
5. Что понимают под термином «живое сечение потока жидкости»?
6. В каком сечении (1-1 или 2-2) больше скорость движения воды, и почему?
7. В каком сечении (1-1 или 2-2) больше давление, и почему?
8. В каком сечении наиболее близко совпадают величины 
и 
, как можно это объяснить?
9. В каком сечении большее расхождение между величинами и , как можно это объяснить?
10.Изменится ли начертание графиков полных и пьезометрических напоров, если проточную часть установки расположить вертикально, а расход 
оставить неизменным?
11.Если диаметр трубы установки в сечении 
больше в два раза диаметра в сечении 
, во сколько раз в узком сечении скоростной напор больше, чем в сечении ?
12.Что такое «элементарная струйка» и какими свойствами она обладает?
13.Что такое «живое сечение потока»?
14.Чем различается живое сечение элементарной струйки и потока?
15.Что такое «линия тока»?
16.Что такое «поверхность тока»?
17.Что такое «трубка тока»?
18.Какие виды движения вы знаете?
19.Есть ли разница в понятиях установившегося и стационарного движения?
20.Что такое гидравлический радиус живого сечения потока?
21.Какая форма канала является наиболее гидравлически выгодной?
22.Что такое «эквивалентный диаметр канала»?
23.Напишите уравнение неразрывности несжимаемой и сжимаемой жидкостей и поясните значение его членов.
24.Какой закон природы отражает уравнение неразрывности?
25.Какой закон природы отражает уравнение Бернулли?
26.Напишите уравнение Бернулли трех видов и поясните значение их членов.
27.Каков геометрический смысл уравнения Бернулли и его членов?
28.Каков энергетический смысл уравнения Бернулли и его членов?
29.Каков физический смысл коэффициента Кориолиса?
30.В каком диапазоне меняется коэффициент Кориолиса?
31.Что такое нивелировочный, пьезометрический, гидравлический уклоны, от каких факторов они зависят, в каких пределах изменяются и могут ли быть равны друг другу?
32.Какие существуют ограничения в применении уравнения Бернулли?
33.Что такое «напор»?
34.Какие виды напоров Вы знаете?
35.Какое движение воды будет в трубопроводе, если диаметр его меняется, а расход остается постоянным?
36.Какое движение будет в трубопроводе постоянного сечения, если расход воды изменяется?
37.Какое движение будет в трубопроводе, если его сечение и расход воды остаются постоянными?
38.Какое движение будет в трубопроводе, если меняются его сечение и расход?
39.Что такое «расход жидкости»?
40.Что измеряет скоростная трубка?
41.Какое давление: абсолютное или избыточное входит в уравнение Бернулли?
42.Как можно замерить скоростной напор?
43.Запишите уравнение Бернулли для потока реальной жидкости и раскройте энергетический смысл его.
44.Почему пьезометр и скоростная трубка показывают разные уровни жидкости при подключении их в одном и том же сечении?
45.Какое начертание имеет график полных напоров в трубе постоянного сечения при движении в ней реальной жидкости?
46.Почему при уменьшении диаметра трубы график пьезометрических напоров понижается?
47.В чем состоит физический смысл коэффициента Кориолиса?
48.Во сколько раз надо уменьшить площадь поперечного сечения потока, чтобы скоростной напор увеличился в четыре раза?
49.Может ли быть давление внутри трубы в сечении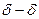 
меньше атмосферного? При каких условиях?
Работа 4 ЭКСПЕРИМЕНТАЛЬНАЯ ИЛЛЮСТРАЦИЯ
Общие сведения
Многочисленными экспериментальными исследованиями установлено, что движение жидкости может происходить или при ламинарном, или при турбулентном режиме.
Ламинарный режим наблюдается при небольших скоростях движения. При этом окрашенные струйки жидкости не перемешиваются, сохраняясь по всей длине потока, т.е. движение жидкости при ламинарном режиме является струйчатым, перемешивание частиц жидкости отсутствует.
Турбулентный режим наблюдается при значительных скоростях и характеризуется интенсивным перемешиванием частиц жидкости, что обусловливает пульсацию скоростей и давления.
Средняя скорость потока, при которой происходит смена режима движения жидкости, называется критической ( 
кр). Величина ее, как показывают опыты в трубопроводах круглого сечения, зависит от рода жидкости, характеризуемого динамической вязкостью m, и плотностью, а также от диаметра трубопровода d. Одновременно опытами установлено, что величина безразмерного алгебраического комплекса, отвечающая критической скорости кр,
(3.1)
от m, r и d не зависит. Reкр(d)=2320 называется критическим числом Рейнольдса. Устойчивый ламинарный режим наблюдается при значениях числа Рейнольдса 
, а турбулентный – при Re(d)> Reкр(d).
Таким образом, число Рейнольдса
(3.2)
является критерием, позволяющим судить о режиме движения жидкости в круглой трубе, работающей полным сечением.
Величину n=m/r, входящую в формулы (3.1) и (3.2), называют кинематическим коэффициентом вязкости жидкости.
Из изложенного следует, что для определения режима движения жидкости в круглом трубопроводе при напорном движении достаточно вычислить по формуле (3.2) число Рейнольдса и сравнить его с критическим.
Знание режима движения жидкости необходимо для правильной оценки потерь напора при гидравлических расчетах. Дело в том, что зависимость потерь напора по длине he от средней скорости имеет разный характер при ламинарном и турбулентном режимах (рисунок 3.1).
Рисунок 3.1 – График зависимости потерь напора по длине hℓ
от средней скорости υ в логарифмической форме
При ламинарном режиме потери напора he пропорциональны средней скорости в первой степени, а при турбулентном - в степени 1, 75 ≤ m≤ 2, 0. Заметим, что с помощью этого графика определяют величину критической скорости 
кр, а через нее - и критическое число Рейнольдса по формуле (3.1).
3.2 Описание установки (рисунок 3.2)
Включает в себя стеклянную трубу расположенную горизонтально 2, в которой изучается движение воды при различных режимах, напорный бак 1, емкость 6 с раствором красителя, подаваемого по капиллярной трубке во входное сечение трубы 2. Для измерения расхода воды в трубе 2 служат мерная емкость 5 и секундомер 7.
Вода в напорный бак 3 подается по питающему трубопроводу из резервуара лаборатории. Для поддержания уровня воды в баке 1 во время опытов на постоянной отметке имеется переливное устройство.
Рисунок 3.2 – Схема установки:
1 – напорный бак;
2 – стеклянная прозрачная трубка;
3 – пьезометры;
4 – регулирующий кран;
5 – мерный бак;
6 – водный краситель;
7 – секундомер;
8 – индикация разности уровней
в пьезометрах (гидравлических потерь)
Регулирование расхода воды, а следовательно, и средней скорости ее движения в трубе 2, осуществляется краном. На трубе 2 имеются пьезометры 3 для определения потерь напора по длине hℓ (по разности их показаний).
Наименование и обозначение
Ед. изм.
Ламин. режим
Турбул. режим
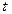
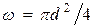
(по справочнику)
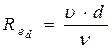
(по справочнику)
8. Открыть кран 13 на винипластовой трубе 2 так, чтобы разность показаний пьезометров 12 составляла не более 0, 3 см, и измерить расход воды и ее температуру. Результаты измерений записать в таблицу 3.2.
9. Сделать ещё девять аналогичных опытов, увеличивая в каждом последующем опыте открытие крана 13 так, чтобы разность показаний пьезометров 12 (потеря напора по длине 
) при этом возрастала примерно в 1, 5…1, 6 раза. Результаты измерений записать в таблицу 3.2.
Таблица 3.2
| № п/п |
Наименование и обозначение Измеряемых и вычисляемых Величин |
Ед. изм. |
Номер опыта | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 1 | Объём воды в мерном сосуде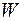 
| см3 | ||||||||||
| 2 | Время наполнения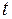 
| с | ||||||||||
| 3 | Расход воды 
| см3/с | ||||||||||
| 4 | Внутренний диаметр трубы 
| см | ||||||||||
| 5 | Площадь попереч. сечения трубы 
| см2 | ||||||||||
| 6 | Средняя скорость потока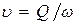 
| см/с | ||||||||||
| 7 | Логарифм средней скорости 
| - | ||||||||||
| 8 | Отметка уровня воды в пьезометре 1 
| см | ||||||||||
| 9 | Отметка уровня воды в пъезометре | см | ||||||||||
| 10 | Потеря напора по длине
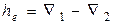
| см | ||||||||||
| 11 | Логарифм потерь напора по длине 
| - | ||||||||||
| 12 | Температура воды | 
| ||||||||||
| 13 | Кинематический коэффициент вязкости воды (по справочнику)
| см2/с | ||||||||||
10. Выполнить все вычисления, предусмотренные таблицами 3.1 и 3.2.
11. Построить в масштабе по данным таблицы 1.5 график 
(рисунок 3.1) и определить с его помощью критическую скорость 
, а через неё и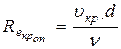 
, а также показатели степени 
и 
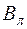и коэффициенты пропорциональности 
и 
.
12. Дать заключение по результатам работы.
3.4 Контрольные вопросы
1. Назовите режимы движения жидкости и укажите их характерные особенности.
2. Поясните, что такое критерий Рейнольдса, и назовите факторы, от которых он зависит.
3. Поясните, что такое критическое число Рейнольдса?
4. Поясните, каким образом при гидравлических расчётах определяют режим движения жидкости и с какой целью?
5. Поясните, что такое критическая скорость, от каких факторов она зависит и как её определяют?
6. Напишите и поясните аналитические зависимости потерь напора по длине от средней скорости потока при ламинарном и турбулентном режимах движения жидкости.
7. Объясните понятия верхней и нижней критической скоростей.
8. Что называется «вязкостью жидкости»?
9. Как связаны динамическая и кинематическая вязкости, каковы их размерности?
10. Напишите уравнения гипотезы Ньютона и поясните значения его членов.
11. Что такое «неньютоновская жидкость»? Приведите примеры таких жидкостей, используемых в строительстве.
12. Напишите формулу Бингама – Шведова и поясните значение её членов.
13. Нарисуйте эпюры скоростей ламинарного и турбулентного течений, а также эпюру напряжения трения при ламинарном движении в трубе.
14. От каких факторов зависит вязкость жидкостей? Расположите их в порядке важности.
15. Как меняется динамическая вязкость жидкости при нагреве?
16. Как меняется кинематическая вязкость жидкости при нагреве?
17. Как меняется кинематическая газа жидкости при нагреве?
18. Как изменится критическая скорость жидкости в трубе при увеличении диаметра трубы вдвое?
19. Как изменится критическое число Рейнольдса жидкости, текущей по трубе, при увеличении диаметра трубы вдвое?
20. Каков физический смысл критерия Рейнольдса?
21. Какова связь средней и максимальной скоростей частиц при ламинарном движении?
22. Что такое «ядро потока»?
23. Что такое «пограничный слой»?
24. Какова структура пограничного слоя и от чего зависит его толщина?
25. Как определить число Рейнольдса для каналов некруглого сечения?
26. В какой из жидкостей разной вязкости, текущих по трубам одного диаметра будет больше критическая скорость?
27. Чему равны силы трения между отдельными слоями жидкости во вращающемся вокруг вертикальной оси сосуде с жидкостью?
28. Сформулируйте гипотезу Ньютона о силе внутреннего трения в жидкости.
29. Как соотносятся между собой критические скорости при движении воды в трубах одинакового диаметра при равных числах Рейнольдса, но при различной температуре?
30. Как влияет внешнее давление на вязкость жидкости?
31. От чего зависит вязкость капельных жидкостей?
32. От чего зависит вязкость газов?
33. Почему при ламинарном режиме движения коэффициент Кориолиса достигает значения двух единиц, а при турбулентном режиме движения - чуть больше единицы?
И МЕСТНЫХ СОПРОТИВЛЕНИЙ
Цель работы:
1. Определить по опытным данным, воспользовавшись формулами (4.2) и (4.3), значение коэффициента гидравлического трения 
и величины коэффициента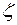 
для трех видов местных сопротивлений.
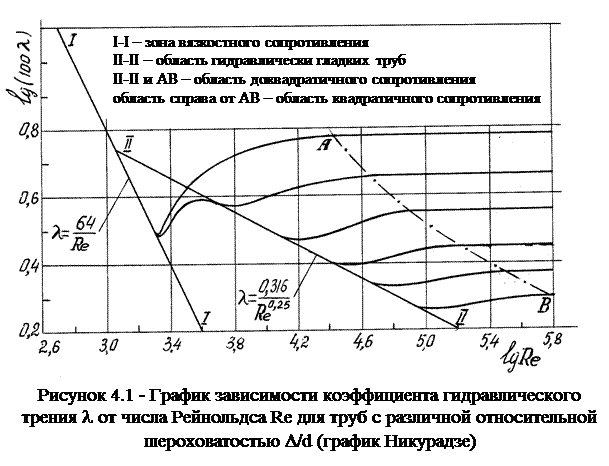
2. Установить, воспользовавшись соотношениями А.Н. Альтшуля или же графиком Никурадзе (рисунок 4.1), области гидравлического сопротивления, в которых работали участки напорного трубопровода.
3. Вычислить значения коэффициентов гидравлического трения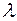 
по соответствующим эмпирическим формулам.
4. Найти справочные значения коэффициентов местных сопротивлений ( 
- по таблице, 
и 
- по формулам (4.4), (4.6)).
5. Оценить сходимость и 
с их расчетными справочными значениями.
Общие сведения
Экспериментальными исследованиями установлено, что при движении жидкости часть полного напора (энергии) затрачивается на преодоление работы вязкостных и инерциональных сил, т.е. возникают потери напора.
При равномерном движении жидкости гидравлическое сопротивление, проявляющееся равномерно по всей длине потока, называют сопротивлением по длине, а вызываемые им потери напора - потерями напора по длине ( hℓ ). Эти потери в круглых трубопроводах, работающих полным сечением, вычисляют по формуле Дарси-Вейсбаха:
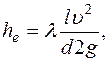(4.1)
где l - безразмерный коэффициент, называемый коэффициентом гидравлического трения ( коэффициентом Дарси ). Величина коэффициента l характеризует гидравлическое сопротивление трубопровода и зависит в общем случае от числа Рейнольдса Re и относительной шероховатости Dэ/d трубопровода, т.е. l=f(Re, Dэ/d);
l, d – длина и внутренний диаметр трубопровода;
– средняя скорость движения потока жидкости.
Величину коэффициента l при гидравлических экспериментах вычисляют по опытным данным из формулы (4.1). При гидравлических же расчетах – по эмпирическим и полуэмпирическим формулам, например, при ламинарном режиме lп=64/Rе, а при турбулентном режиме движения и работе трубопровода в области доквадратичного сопротивления – по формуле А.Д. Альтшуля:
. (4.2)
Величину абсолютной эквивалентной шероховатости Dэ при расчетах берут из справочной литературы в зависимости от материала трубопровода и состояния его внутренней поверхности. Например, для труб из органического стекла Dэ=0, 006 мм, а для стальных водопроводных умеренно заржавленных труб Dэ=0, 20…0, 50 мм.
Область гидравлического сопротивления при расчетах определяют или непосредственно по графикам l=f(Re, Dэ/d), полученным опытным путем для труб из различных материалов и приведенным в справочной литературе, например, по графику Никурадзе (рисунке 4.1), или же с помощью соотношений 
и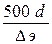 
, предложенных А. Д. Альтшулем на основе использования упомянутых графиков. В последнем случае поступают следующим образом.
Вычисляют соотношения 10d/Dэ и 500d/Dэ и сравнивают их с числом Рейнольдса Re = Vd/n. При этом, если 
, трубопровод работает в области гидравлически гладких труб. Если 
, трубопровод работает в области квадратичного сопротивления. Если же 10d/Dэ ≤ Re ≤ 500dэ/Dэ, трубопровод работает в области доквадратичного сопротивления.
Следует иметь в виду, что для каждой области гидравлического сопротивления предложены и используются при гидравлических расчетах свои формулы для вычисления коэффициента l.
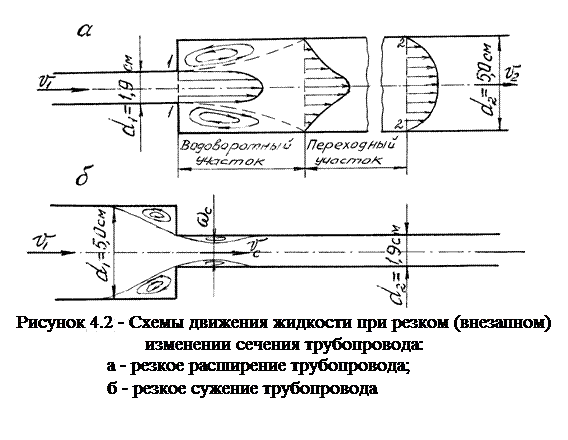
Другой вид гидравлических сопротивлений, возникающих в местах резкого изменения конфигурации потока, называют местными сопротивлениями, а вызываемые ими потери напора - местными потерями напора (hм).
При прохождении через любое местное сопротивление поток жидкости деформируется (рисунок 4.2 а, б, в), вследствие чего движение становится неравномерным резко изменяющимся, для которого характерны:
а) значительное искривление линий потока и кривых сечений потока;
б) отрывы транзитной струи от стенок трубопровода (ввиду действия закона инерции) и возникновения в местах отрыва устойчивых водовязатов;
в) повышенная (по сравнению с равномерным движением) пульсация скоростей и давлений;
г) изменение формы (переформирование) эпюр скоростей.
Местные потери напора при гидравлических расчетах вычисляют по формуле Вейсбаха:
, (4.3)
где 
- безразмерный коэффициент, называемый коэффициентом местного сопротивления;
- средняя скорость потока в сечении за местным сопротивлением, т.е. ниже по течению (если скорость , как исключение, принимается перед местным сопротивлением, это обязательно оговаривается).
Величина коэффициента 
зависит в общем случае от числа Рейнольдса 
и от конфигурации, т.е. формы проточной части местного сопротивления. В частном случае, когда трубопровод, на котором расположено местное сопротивление, работает в области квадратичного сопротивления, величина коэффициента 
от 
не зависит.
Величину 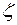для каждого вида местного сопротивления определяют по данным гидравлических экспериментов, пользуясь формулой (4.3), полученные таким образом значения коэффициентов 
для различных видов местных сопротивлений (обычно при квадратичной области сопротивления) приводятся в справочной и специальной литературе, откуда и берутся при гидравлических расчётах. Исключением является резкое расширение и резкое сужение трубопровода (рисунок 4.2 а, б), для которых численные значения коэффициента 
определяются по формулам, полученным теоретически. Так, при резком расширении трубопровода, когда средняя скорость в формуле (4.3) взята перед местным сопротивлением, т.е.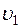 
,
, (4.4)
если же скорость берется за местным сопротивлением, т.е. 
,
(4.5)
Коэффициент сопротивления при резком сужении трубопровода ( 
) принято относить к скорости после сужения. При этом
, (4.6)
где 
- коэффициент сжатия струи.
Описание установки
Установка (рисунок 4.3) представляет собой систему напорных трубопроводов с последовательно расположенными на нем гидравлическими сопротивлениями (по длине и местными). К каждому гидравлическому сопротивлению подключено по два пьезометра (перед и за ним). Все пьезометры для удобства работы выведены на щит 4. Для регулирования расхода воды 
в системе служит вентиль 2. Величина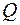 
измеряется с помощью мерного бака 1 и секундомера. 3. Подача воды в систему осуществляется из питающего резервуара. Постоянный уровень воды в резервуаре (для обеспечения установившегося движения в системе) поддерживается переливным устройством.
Рисунок 4.3 – Схема установки:
1 – мерный бак;
2 – вентиль для регулирования расхода воды;
3 – секундомер;
4 – пьезометры;
5 – напорный питающий бак;
D1 и D2 – диаметры трубопроводов
Участок прямой трубы 2
Внезап.
Сужение
Потока
Внезап.
Расшир.
Потока
Участок прямой трубы 3
10
11
12
10
11
12
13
13
4.4 Контрольные вопросы
1. Какова природа гидравлических потерь по длине трубопровода?
2. От каких параметров зависит коэффициент гидравлических сопротивлений по длине?
3. Какова размерность коэффициента гидравлических потерь по длине?
4. Назовите характерные области гидравлических сопротивлений, в которых коэффициент 
имеет свою закономерность?
5. В какой степени от скорости 
зависят гидравлические потери по длине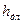 
в характерных областях гидросопротивлений?
6. Почему в настоящей работе гидравлические потери по длине определяют по разности показаний пьезометров, установленных на начальном и конечном участках трубопровода?
7. Зачем при проектировании водопровода рассчитывают его гидравлическое сопротивление?
8. Есть ли разница в понятиях «потери по длине» и «потери на трение»?
9. Какие факторы влияют на потери по длине?
10. Напишите формулу Дарси-Вейсбаха и поясните значение её членов.
11. Что такое «абсолютная», «равномерная», «неравномерная», «эквивалентная» и «относительная» шероховатости стенок канала?
12. Что такое «относительная гладкость стенок канала»?
13. Какая стенка называется «гидравлически гладкой»?
14. Какая стенка называется «вполне шероховатой»?
15. От каких факторов зависит коэффициент Дарси в различных областях сопротивления?
16. Как определить границы зон сопротивления?
17. Как увязать потери напора в потоке с законом сохранения энергии?
18. Как изменятся потери напора при ламинарном течении и постоянном расходе, если диаметр трубы увеличится вдвое?
19. Как определяется коэффициент Дарси в различных областях сопротивления?
20. В каких областях сопротивления коэффициент Дарси наиболее сильно зависит от числа Рейнольдса и относительной шероховатости?
21. Во сколько раз увеличатся потери напора на трение при ламинарном режиме, если расход увеличится в два раза?
22. Во сколько раз увеличатся потери напора на трение во вполне шероховатых трубах, если абсолютная шероховатость стенок возрастет в 4 раза?
23. В какой области гидравлических сопротивлений коэффициент Дарси в большей степени зависит от числа Рейнольдса?
24. Нарисуйте графики Никурадзе и укажите основные зоны гидравлических сопротивлений.
25. В какой области гидравлического сопротивления при постоянном расходе и постоянной шероховатости гидравлические потери более всего зависят от диаметра трубы?
26. Что такое «гидравлически гладкие трубы»?
27. Может ли одна и та же труба быть «гидравлически гладкой» и «вполне шероховатой»? При каких условиях?
28. Как изменится коэффициент Дарси при ламинарном режиме движения и постоянном расходе жидкости, если диаметр трубы увеличить в два раза?
29. Что такое «зона квадратичного сопротивления»?
32. От каких факторов зависят потери напора в переходной зоне сопротивления?
33. Почему линии графика полных напоров не могут подниматься вверх, а линии графика пьезометрических напоров на трубе переменного сечения поднимаются вверх?
34. Почему на некоторых участках графика полных напоров линии практически горизонтальны?
35. В каком случае гидравлические потери можно определить по разности пьезометрических напоров?
36. Что такое «гидравлический» и «пьезометрический» уклоны?
37. Совместным решением каких уравнений получена формула Борда-Карно?
38. Что означает ступенька на графике полных напоров?
39. Оказывают ли влияние на общую величину гидравлических потерь энергии близко расположенные местные сопротивления?
40. Если на внезапном расширении больший диаметр в два раза больше диаметра трубы меньшего сечения, то во сколько раз отличаются скоростные напоры до внезапного расширения и после него?
Журнал для лабораторных работ по гидравлике
( специальность ЗТ и МАЭС)
Студент:
Группа
Последнее изменение этой страницы: 2019-04-09; Просмотров: 899; Нарушение авторского права страницы
.
.
. 
. 
движения жидкости): 
, равным силе на единице длины контура свободной поверхности. Значения 
и 
р, . 103 
,
.
в шкале термометра и измерить расстояние 
, где г - радиус капилляра термометра.
и сравнить его со справочным значением β T (табл. 1.1). Значения используемых величин занести в таблицу 1.2.
,
см
см
см 
. (3.1)
- гидростатический напор; 
- полный напор в рассматриваемом сечении струйки; 
- потеря полного напора, т.е. часть полного напора, затраченная на преодоление гидравлических сопротивлений на пути между сечениями I-I и II-II.
- полная удельная энергия; 
- удельная потенциальная энергия; 
. 
, (3.2)
- скоростной напор, отвечающий средней скорости 
потока жидкости в рассматриваемом живом сечении (здесь Q, - расход потока жидкости, w - площадь живого сечения потока); 