Электрический пробой газа

- процесс перехода несамостоятельного газового разряда в самостоятельный.

Самостоятельный газовый разряд бывает 4-х типов:

1. тлеющий - при низких давлениях(до нескольких мм рт.ст.) -наблюдается в газосветных трубках и газовых лазерах.
2. искровой - при нормальном давлении и высокой напряженности электрического поля (молния - сила тока до сотен тысяч ампер).
3. коронный - при нормальном давлении в неоднородном электрическом поле ( на острие ).
4. дуговой - большая плотность тока, малое напряжение между электродами ( температура газа в канале дуги -5000-6000 градусов Цельсия); наблюдается в прожекторах, проекционной киноаппаратуре.

Эти разряды наблюдаются:

тлеющий - в лампах дневного света;
искровой - в молниях;
коронный - в электрофильтрах, при утечке энергии;
дуговой - при сварке, в ртутных лампах.

37

Плазма

- это четвертое агрегатное состояние вещества с высокой степенью ионизации за счет столкновения молекул на большой скорости при высокой температуре; встречается в природе: ионосфера - слабо ионизированная плазма, Солнце - полностью ионизированная плазма; искусственная плазма - в газоразрядных лампах.

Плазма бывает:

Низкотемпературная - при температурах меньше 100 000К;
высокотемпературная - при температурах больше 100 000К.

Основные свойства плазмы:

- высокая электропроводность
- сильное взаимодействие с внешними электрическими и магнитными полями.

При температуре

любое вещество находится в состоянии плазмы.

 

Понятие о плазме

В газовом разряде возникает большое количество положительных ионов вследствие высокой эффективности ударной ионизации, причем концентрация ионов и электронов одинакова. Такая система из электронов и положительных ионов, распределенных с одинаковой концентрацией, называется плазмой. Термин «плазма» был введен в 1929 г. американскими физиками И. Ленгмюром и Л. Тонксом.

Плазма, возникающая в газовом разряде, носит название газоразрядной; к ней относятся положительный столб тлеющего разряда, канал искрового и дугового разрядов.

Положительный столб представляет собой так называемую неизотермическую плазму. В такой плазме средние кинетические энергии электронов, ионов и нейтральных молекул (атомов) различны.

Вспомним связь между средней кинетической энергией молекул идеального газа (давление газа в тлеющем разряде невелико, поэтому его можно считать идеальным) и температурой

Можно утверждать, что температуры компонентов плазмы различны. Так, электронная температура в тлеющем разряде в неоне при давлении 3 мм. рт. ст., порядка 4∙10 ⁴ К, а температура ионов и атомов 400 К, причем температура ионов несколько выше атомной температуры.

Плазма, в которой выполняется равенство: (где индексы «э», «и», «а» относятся к электронам, ионам, атомам) называется изотермической. Такая плазма имеет место при ионизации с помощью высокой температуры (дуга, горящая при атмосферном и выше давлении, искровой канал); например, в дуге сверхвысокого давления (до 1000 атм.) температура плазмы достигает 10000 К, температура плазмы при термоядерном взрыве – порядка нескольких десятков миллионов градусов, в установке «ТОКАМАК» для исследования термоядерных реакций – порядка 7∙10⁶ K.

Плазма может возникнуть не только при прохождении тока через газ. Газ можно перевести в плазменное состояние и путем его нагревания до высоких температур. Внутренние области звезд (в том числе и солнце) находятся в плазменном состоянии, температуры которых достигают 10 ⁸ К

Кулоновское дальнодействующее взаимодействие заряженных частиц в плазме приводит к качественному своеобразию плазмы, позволяющему считать ее особым, четвертым агрегатным состоянием вещества.

Важнейшие свойства плазмы:

• сильное взаимодействие с внешними магнитными и электрическими полями, связанное с ее высокой электропроводностью;
• специфическое коллективное взаимодействие частиц плазмы, осуществляющееся через усредненные электрические и магнитные поля, которые создают сами эти частицы;
• благодаря коллективным взаимодействиям плазма ведет себя как своеобразная упругая среда, в которой легко возбуждаются и распространяются различного рода колебания и волны (например, ленгмюровские колебания плазмы);
• во внешнем магнитном поле плазма ведет себя как диамагнитная среда;
• удельная электрическая проводимость σ полностью ионизованной плазмы не зависит от плотности плазмы и увеличивается с ростом термодинамической температуры, пропорционально . При Т ≥ 10⁷ К, σ столь велика, что плазму можно приближенно считать идеальным проводником ( ).

Плазма – наиболее распространенное состояние вещества во Вселенной. Солнце и другие звезды состоят из полностью ионизованной высокотемпературной плазмы. Основной источник энергии излучения звезд – термодинамические реакции синтеза, протекающие в недрах звезд при огромных температурах. Холодные туманности и межзвездная среда также находятся в плазменном состоянии. Они представляют собой низкотемпературную плазму, ионизация которой происходит, главным образом, путем фотоионизации под действием ультрафиолетового излучения звезд. В околоземном пространстве слабоионизованная плазма находится в радиационных поясах и ионосфере Земли. С процессами, происходящими в этой плазме, связаны такие явления, как магнитные бури, нарушения дальней радиосвязи и полярные сияния.

Низкотемпературная газоразрядная плазма, образующаяся при тлеющем, искровом и дуговом разрядах в газах, широко используется в различных источниках света, в газовых лазерах, для сварки, резки, плавки и других видов обработки металлов.

Основной практический интерес к физике плазмы связан с решением проблемы управляемого термоядерного синтеза – процесс слияния легких атомных ядер при высоких температурах в управляемых условиях. Энергетический выход реактора составляет 10⁵ кВт/м³ в реакции

)

при плотности плазмы 10⁵ см^-3 и температуре 10⁸ К.

38

Свободные гармонические колебания в колебательном контуре

Среди исследований различных электрических явлений особое место занимают исследования электромагнитных колебаний. При колебательном процессе электрические физические величины (заряды, токи) периодически изменяются и процесс сопровождается взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний применяется колебательный контур — цепь, которая состоит из последовательно включенных резистора сопротивлением R, катушки индуктивностью L, и конденсатора емкостью С. Исследуем последовательные стадии колебательного процесса в идеализированном контуре, у которого сопротивление пренебрежимо мало (R≈0). Для возбуждения колебаний в контуре конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Следовательно, в начальный момент времени t=0 (рис. 1а) между обкладками конденсатора появится электрическое поле, энергия которого равна Q2/(2C) . Если конденсатор замкнуть на катушку индуктивности, то он начнет разряжаться, и в контуре начнет течь возрастающий со временем ток I. В результате энергия электрического поля будет падать, а энергия магнитного поля катушки (она равна (1/2)LI2 ) - увеличиваться. Так как R≈0, то, используя закон сохранения энергии, полная энергия поскольку полная энергия на нагревание не тратится. Поэтому в момент t=(1/4)T, когда конденсатор полностью разрядится, энергия электрического поля станет равной нулю, а энергия магнитного поля (а следовательно, и ток) достигает максимального значения (рис. 1б). Далее, начиная с этого момента ток в контуре будет уменьшаться; значит, начнет уменьшаться магнитное поле катушки, и в ней индуцируется ток, который течет (по правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Далее, начнет перезаряжаться конденсатор, появится электрическое поле, которое будет стремиться ослабить ток, который в конце концов станет равным нулю, а заряд на обкладках конденсатора станет максимальным (рис. 1в). Далее те же процессы будут протекать в обратном направлении (рис. 1г) и к моменту времени t=Т система придет в первоначальное состояние (рис. 1а). После этого рассмотренный цикл разрядки и зарядки конденсатора будет повторяться. Если бы в контуре потерь энергии не было, то совершались бы периодические незатухающие колебания, т.е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, сила тока I, текущего через катушку индуктивности и напряжение U на конденсаторе . Значит, в контуре появляются электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей. С электрическими колебаниями в колебательном контуре можно провести аналогию с механическими колебаниями маятника (рис. 1 внизу), которые сопровождаются взаимными превращениями кинетической и потенциальной энергий маятника (на рисунке Е - кинетическая энергия, П - потенцияльная). В данном случае энергия электрического поля конденсатора Q2/(2C) аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ2/2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L аналогична массе m, а сопротивление контура — силе трения, которая действуюет на маятник. По закону Ома, для контура, который содержит резистор сопротивлением R, катушку индуктивностью L, и конденсатор емкостью С где IR—напряжение на резисторе, UC = Q/C - напряжение на конденсаторе, ξs = -L(dI/dt) – э.д.с. самоиндукции, которая возникает в катушке при протекании в ней переменного тока (ξs – единственная э.д.с. в контуре). Значит, 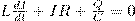(1) Разделив формулу (1) на L и подставив и получим дифференциальное уравнение колебаний заряда Q в контуре: (2) В рассматриваемом колебательном контуре внешние э.д.с. отсутствуют, значит колебания в контуре представляют собой свободныеколебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре будут гармоническими. Тогда из (2) найдем дифференциальное уравнение свободных гармонических колебаний заряда в контуре: Из формулы (1) следует, что заряд Q гармонически колеблеься по закону 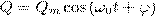(3) где Qm — амплитуда колебаний заряда конденсатора с циклической частотой ω0, которая называется собственной частотой контура, т. е. (4) и периодом 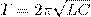(5) Выражение (5) впервые было получено У. Томсоном и называется формулой Томсона. Сила тока в колебательном контуре (6) где Im = ω0Qm — амплитуда силы тока. Напряжение на конденсаторе равно (7) где Um=Qm/C - амплитуда напряжения. Из формул (3) и (6) вытекает, что колебания тока I опережают по фазе колебания заряда Q на π/2, т.е., когда ток равен максимальному значению, заряд (а также и напряжение (7)) обращается в нуль, и наоборот.

39

Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания

Рассмотрим свободные затухающие колебания – колебания, у которых амплитуды из-за потерь энергии колебательной системой с течением времени убывают. Простейшим механизмом убывания энергии колебаний есть ее превращение в теплоту вследствие трения в механических колебательных системах, а также потерь, связанных с выделением теплоты, и излучения электромагнитной энергии в электрических колебательных системах. Вид закономерностей затухания колебаний задается свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, параметры которых, определяющие физические свойства системы, в ходе процесса остаются неизменными. Например, линейными системами являются пружинный маятник при малых растяжениях пружины (когда выполняется закон Гука), колебательный контур, у которого сопротивление, индуктивность и емкость не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются аналогичными линейными дифференциальными уравнениями, что дает основания подходить к изучению колебаний различной физической природы с единой точки зрения, а также моделировать их, в том числе и на ЭВМ. Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как (1) где s – колеблющаяся величина, которая описывает тот или иной физический процесс, δ = const — коэффициент затухания, ω0 - циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения (1) запишем в виде (2) где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем (3) Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положителньного коэффициента: (4) (если (ω02 - σ2)>0, то такое обозначение мы вправе сделать). Тогда получим выражение , у которого решение будет функция 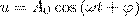. Значит, решение уравнения (1) в случае малых затуханий (ω02 >> σ2 ) (5) где (6) — амплитуда затухающих колебаний, а А0 — начальная амплитуда. Выражение (5) представлено графики рис. 1 сплошной линией, а (6) — штриховыми линиями. Промежуток времени τ = 1/σ, в течение которого амплитуда затухающих колебаний становится мешьше в е раз, называется временем релаксации.   Рис.1 Затухание не дает колебаниям быть периодичными и, строго говоря, к ним нельзя применять понятие периода или частоты. Но если затухание мало, то можно условно использовать понятие периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис. 1). В этом случае период затухающих колебаний с учетом выражения (4) будет равен Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, которые отличаются на период, то отношение называется декрементом затухания, а его логарифм (7) — логарифмическим декрементом затухания; Ne — число колебаний, которые совершаются за время уменьшения амплитуды в е раз. Логарифмический декремент затухания является постоянной величиной для данной колебательной системы. Для характеристики колебательной системы также применяют понятие добротности Q, которая при малых значениях логарифмического декремента будет равна (8) (так как затухание мало (ω02 >> σ2 ), то T принято равным Т0). Из формулы (8) вытекает, что добротность пропорциональна числу колебаний Ne, которые система совершает за время релаксации. Выводы и уравнения, полученные для свободных затухающих колебаний линейных систем, можно использовать для колебаний различной физической природы — механических (в качестве примера возьмем пружинный маятник) и электромагнитных (в качестве примера возьмем электрический колебательный контур). 1. Свободные затухающие колебания пружинного маятника. Для пружинного маятника массой m, который совершает малые колебания под действием упругой силы F= -kx, сила трения прямо пропорциональна скорости, т. е. где r — коэффициент сопротивления; знак минус говорит о том, что сила трения и скорость противоположно направлены. При этих условиях закон движения маятника (9) Используя формулу и считая, что коэффициент затухания равен (10) получим полностью идентичное уравнению (1) дифференциальное уравнение затухающих колебаний маятника: Из выражений (1) и (5) следует, что колебания маятника удовлетворяют уравнению где частота (см. (4)). Добротность пружинного маятника, используя (8) и (10), . 2. Свободные затухающие колебания в электрическом колебательном контуре. Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R≠0) , как известно Учитывая формулу собственной частоты колебательного контура и принимая коэффициент затухания равным (11) дифференциальное уравнение колебаний заряда Q (см. раздел "Свободные гармонические колебания в колебательном контуре") можно записать в аналогичном уравнению (1) виде Из зависимостей (1) и (5) следует, что колебания заряда подчиняются закону (12) с частотой, используя (4), равной (13) меньшей собственной частоты контура ω0 . При R=0 формула (13) становится формулой (4). Логарифмческий декремент затухания задается формулой (7), а добротность колебательного контура (8) (14) Отметим в заключение, что при увеличении коэффициента затухания δ период затухающих колебании увеличивается и при δ=ω0равен бесконечности, т. е. движение перестает быть периодическим. В этом случае колеблющаяся величина асимптотически стремится к нулю, когда t→∞. Данный процесс не будет колебательным. Он называется апериодическим. Значительный интерес для техники представляет возможность сохранять колебания незатухающими. Для этого необходимо восполнять каким-либо образом потери энергии реальной колебательной системы. Особенно важны и широко используются так называемыеавтоколебания — незатухающие колебания, которые поддерживаются в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний задаются самой системой. Автоколебания принципиально отличаются от свободных незатухающих колебаний, которые происходят без действия сил, а также от вынужденных колебаний (см. следующий раздел), которые происходят под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями). Примером автоколебательной системы являются часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, которая передавается при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также появляются вследствие автоколебаний, поддерживаемых воздушной струёй. Автоколебательными системами являются также паровые турбины, двигатели внутреннего сгорания, ламповый генератор и т. д.

39

⇐ Предыдущая123456Следующая ⇒

Поделиться: