
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Досяжність і зв’язність. Компоненти зв’язності.
Означення. Граф G називається зв'язним, якщо будь-яка пара його вершин з'єднана маршрутом. Теорема (про число маршрутів, які з’єднують будь-яку пару вершин графа). Нехай - матриця суміжності графа - матриця суміжності графа  і і  . Тоді . Тоді  є число маршрутів довжини є число маршрутів довжини  від від 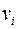 до до  .Наслідок 1. Маршрут від вершини .Наслідок 1. Маршрут від вершини 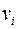 до вершини до вершини  ( (  ) в графі ) в графі  існує тоді і тільки тоді, коли ( існує тоді і тільки тоді, коли ( 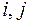 )-й елемент матриці )-й елемент матриці  не дорівнює нулю.Наслідок 2. Маршрут від вершини не дорівнює нулю.Наслідок 2. Маршрут від вершини 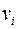 до вершини до вершини  в графі в графі  існує тоді і тільки тоді, коли ( існує тоді і тільки тоді, коли ( 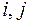 )-й елемент матриці )-й елемент матриці  не дорівнює нулю.Означення. Нехай не дорівнює нулю.Означення. Нехай  – деяка матриця. Булевим відображенням для матриці – деяка матриця. Булевим відображенням для матриці  називається відображення називається відображення 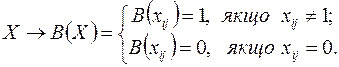 Означення. Матрицею досяжності графа Означення. Матрицею досяжності графа  називається матриця називається матриця  де де  – число вершин, – число вершин,  – одинична матриця, – одинична матриця,  – булево відображення.Маршрут від вершини – булево відображення.Маршрут від вершини 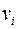 до вершини до вершини  існує в графі існує в графі  тоді й тільки тоді, коли тоді й тільки тоді, коли  дорівнює 1.Граф дорівнює 1.Граф  є зв’язним тоді й тільки тоді, коли для всіх є зв’язним тоді й тільки тоді, коли для всіх  (матриця досяжності заповнена одиницями). (матриця досяжності заповнена одиницями). Властивість зв'язности можна розглянути як бінарне відношення, яке: а) рефлексивне: вершина б) симетричне: якщо вершина в) транзитивне: якщо вершина Відношення зв’язності є відношенням еквівалентності, тобто воно розбиває множину вершин графа на класи, які попарно не перерізаються. Оскільки кожна множина  - розбиття графа - розбиття графа  , обумовлене відношенням зв’язності. Число , обумовлене відношенням зв’язності. Число  називається числом зв’язності графа називається числом зв’язності графа 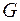 .Означення. Компонентами зв’язності графа .Означення. Компонентами зв’язності графа  називаються підграфи називаються підграфи  графа, породжені класами еквівалентності. графа, породжені класами еквівалентності. Компоненти графа  визначається аналогично графам. Але відзначимо, що для орграфів відношення зв’язності не є відношенням еквівалентності на множині вершин визначається аналогично графам. Але відзначимо, що для орграфів відношення зв’язності не є відношенням еквівалентності на множині вершин  і, отже, не здійснює розбиття множини і, отже, не здійснює розбиття множини  .Для орграфів поняття зв’язності є більше змістовним, чим для неорієнтованих графів. Розрізняють три важливих типи зв’язності орграфа:а) орграф .Для орграфів поняття зв’язності є більше змістовним, чим для неорієнтованих графів. Розрізняють три важливих типи зв’язності орграфа:а) орграф  сильно зв'язний, якщо для кожної пари різних вершин сильно зв'язний, якщо для кожної пари різних вершин  , ,  з з  існує шлях (орієнтований ланцюг) з існує шлях (орієнтований ланцюг) з 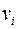 в в  і з і з  в в 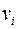 .б) орграф .б) орграф 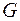 односторонньо зв'язний, якщо для кожної пари різних вершин односторонньо зв'язний, якщо для кожної пари різних вершин  , ,  з з  існує шлях з існує шлях з 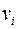 в в  або з або з  в в 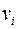 .в) орграф .в) орграф 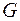 слабкозв'язний, якщо граф, отриманий з слабкозв'язний, якщо граф, отриманий з  скасуванням орієнтації є зв’язним.Очевидно, що справедливі наслідки:G сильно зв'язний скасуванням орієнтації є зв’язним.Очевидно, що справедливі наслідки:G сильно зв'язний  G односторонньо зв'язний G односторонньо зв'язний  G слабко зв'язний.Приклад. G слабко зв'язний.Приклад. 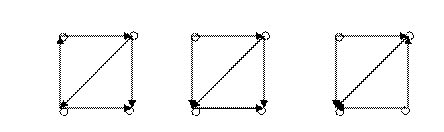 Сильна, одностороння і слаба зв'язність.У термінах матриці зв’язності Сильна, одностороння і слаба зв'язність.У термінах матриці зв’язності  орграф G сильно зв'язний тоді і тільки тоді, коли орграф G сильно зв'язний тоді і тільки тоді, коли  для всіх для всіх  ; G односторонньо зв'язний тоді й тільки тоді, коли ; G односторонньо зв'язний тоді й тільки тоді, коли  або або  для всіх для всіх  .Твердження. Орграф є сильно зв'язний тоді й тільки тоді, коли в ньому є остовний циклічний маршрут.Означення. Компонентами сильної зв’язності орграфа .Твердження. Орграф є сильно зв'язний тоді й тільки тоді, коли в ньому є остовний циклічний маршрут.Означення. Компонентами сильної зв’язності орграфа  називаються його максимальні сильно зв'язні підграфи.Кожна вершина орграфа належить тільки одній компоненті сильної зв’язності. Якщо вершина не зв’язана з іншими, то вважають, що вона сама утворює компоненту сильної зв’язності.Означення. Конденсацією називаються його максимальні сильно зв'язні підграфи.Кожна вершина орграфа належить тільки одній компоненті сильної зв’язності. Якщо вершина не зв’язана з іншими, то вважають, що вона сама утворює компоненту сильної зв’язності.Означення. Конденсацією  орграфа орграфа 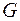 (або фактор-графом) називається орграф, який отриманий стягуванням в одну вершину кожної компоненти сильної зв’язності орграфа (або фактор-графом) називається орграф, який отриманий стягуванням в одну вершину кожної компоненти сильної зв’язності орграфа  .Приклад орграфа ті його конденсації: .Приклад орграфа ті його конденсації: 
Операції над графами За допомогою різних операцій можна будувати графи з більш простих, переходити від одного графа до іншого, більш простого, розбивати граф на більш прості, у заданому класі графів переходити від одного графа до іншого і т.д. Найбільш вживаними одномісними операціями є: 1. Операція вилучення вершини з графа 2. Операція вилучення ребра з графа 3. Операція додавання вершини до графа 4. Операція додавання ребра до графа Вилучаючи ребро і додаючи нову вершину, що з'єднується ребром з кожною вершиною вилученого ребра, робимо операцію підрозділу ребра графа Приклад.
G1=(V1, E1)
V2=V1 V {V6} E2=(E1\{(V1,V5)})U{(V1,V6);
G2 Означення.Граф G2 називається підрозділом графа G1, якщо він може бути отриманий з G1 шляхом застосування кінцевого числа операцій підрозділу ребер. Найбільш уживаними 2-місними операціями над графами є об'єднання і декартовий добуток. Означення. Нехай G1=(V1,E1); G2=(V2,E2) – два графи таких, що V1∩V2=Ø, E1∩E2=Ø. Об'єднанням графів Приклад.
Нехай задані графи Означення.Декартовим добутком графів Приклад.
Види графів |
||||||||||||||||||||||||||||||||||||||||||||
Последнее изменение этой страницы: 2019-04-10; Просмотров: 404; Нарушение авторского права страницы