Описание интегральной математической модели.
Основная система дифференциальных уравнений интегральной математической модели пожара в помещении, описывающих процесс изменения состояния среды, заполняющей помещение, имеет вид;
 , (1.5)
, (1.5)
 (1.6)
(1.6)
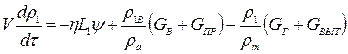 ; (1.7)
; (1.7)
 ; (1.8)
; (1.8)
 (1.9)
(1.9)
 , (1.10)
, (1.10)
где  - объем первого помещения, м3;
- объем первого помещения, м3;
 - среднеобъемная плотность газовой среды в первом помещении, кг/м3;
- среднеобъемная плотность газовой среды в первом помещении, кг/м3;
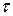 - время, с;
- время, с;
 - скорость выгорания (скорость газификации) горючего материала в рассматриваемый момент времени, в первом помещении, кг/с;
- скорость выгорания (скорость газификации) горючего материала в рассматриваемый момент времени, в первом помещении, кг/с;
 - массовый расход поступающего воздуха из окружающей атмосферы в помещение, который имеет место в рассматриваемый момент времени процесса развития пожара, кг/с;
- массовый расход поступающего воздуха из окружающей атмосферы в помещение, который имеет место в рассматриваемый момент времени процесса развития пожара, кг/с;
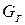 - массовый расход газов, покидающих помещение через проемы в рассматриваемый момент времени, кг/с;
- массовый расход газов, покидающих помещение через проемы в рассматриваемый момент времени, кг/с;
 и
и  - массовые расходы, создаваемые приточно-вытяжной вентиляцией, кг/с;
- массовые расходы, создаваемые приточно-вытяжной вентиляцией, кг/с;
 - массовый расход огнетушащего вещества, кг/с;
- массовый расход огнетушащего вещества, кг/с;
 - среднеобъемное давление, Н/м2
- среднеобъемное давление, Н/м2
 - отношение изобарной и изохорной теплоемкостей идеального газа (показатель адиабаты);
- отношение изобарной и изохорной теплоемкостей идеального газа (показатель адиабаты);
 - коэффициент полноты сгорания (
- коэффициент полноты сгорания ( 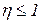 );
);
 - низшая теплота сгорания, Дж/кг;
- низшая теплота сгорания, Дж/кг;
 - энтальпия продуктов газификации горючего материала, Дж/кг;
- энтальпия продуктов газификации горючего материала, Дж/кг;
 ,
, 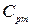 ,
,  - изобарные теплоемкости воздуха, газов в помещении и огнетушащего вещества (инертного газа) соответственно, Дж/(кг К);
- изобарные теплоемкости воздуха, газов в помещении и огнетушащего вещества (инертного газа) соответственно, Дж/(кг К);
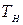 ,
,  ,
,  - температура воздуха (
- температура воздуха (  ), газовой среды в первом и огнетушащего вещества соответственно, К;
), газовой среды в первом и огнетушащего вещества соответственно, К;
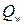 - тепловой поток, поглощаемый ограждающими конструкциями, Вт;
- тепловой поток, поглощаемый ограждающими конструкциями, Вт;
 - тепловой поток излучаемый через проемы, Вт;
- тепловой поток излучаемый через проемы, Вт;
 - тепловой поток, поступающий от системы отопления, Вт;
- тепловой поток, поступающий от системы отопления, Вт;
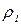 - среднеобъемная парциальная плотность кислорода, кг/м3;
- среднеобъемная парциальная плотность кислорода, кг/м3;
 - стехиометрический коэффициент для кислорода (количество кислорода, необходимое для сгорания единицы массы горючего материала), кг/кг;
- стехиометрический коэффициент для кислорода (количество кислорода, необходимое для сгорания единицы массы горючего материала), кг/кг;
 - парциальная плотность кислорода в поступающем воздухе, кг/м3;
- парциальная плотность кислорода в поступающем воздухе, кг/м3;
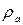 - плотность атмосферы (воздуха) (
- плотность атмосферы (воздуха) (  ), кг/м3;
), кг/м3;
 - среднеобъемная парциальная плотность токсичного продукта горения, кг/м3;
- среднеобъемная парциальная плотность токсичного продукта горения, кг/м3;
 - стехиометрический коэффициент для продукта горения (количество продукта горения, образующегося при сгорании единицы массы горючего материала), кг/кг;
- стехиометрический коэффициент для продукта горения (количество продукта горения, образующегося при сгорании единицы массы горючего материала), кг/кг;
 - среднеобъемная оптическая плотность дыма, Нп/м.
- среднеобъемная оптическая плотность дыма, Нп/м.
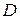 - дымообразующая способность Нп-м2/кг;
- дымообразующая способность Нп-м2/кг;
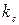 - коэффициент седиментации (оседание) частиц дыма на поверхностях ограждающих конструкций, Нп/м;
- коэффициент седиментации (оседание) частиц дыма на поверхностях ограждающих конструкций, Нп/м;
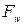 - площадь поверхности ограждений (потолка, пола, стен), м2.
- площадь поверхности ограждений (потолка, пола, стен), м2.
Анализ исходных данных показывает, что в уравнениях (1.5) –(1.10) можно положить
 =0,
=0,  =0,
=0,  =0,
=0,  =0. (1.11)
=0. (1.11)
С учётом условий (1.11), задачи определения парциальных плотностей токсичных газов: диоксида углерода, оксида углерода уравнения пожара запишутся в следующем виде
 , (1.13)
, (1.13)
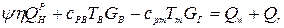 (1.14)
(1.14)
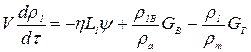 ; (1.15)
; (1.15)
 ; (1.16)
; (1.16)
 ; (1.17)
; (1.17)
 . (1.18)
. (1.18)
 , (1.19)
, (1.19)
Начальные условия для дифференциальных уравнений записываются следующим образом:
при  .
.
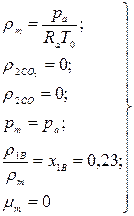 (1.20)
(1.20)
где  - начальная температура в помещении (
- начальная температура в помещении ( 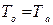 по условию), К;
по условию), К;
 - газовая постоянная воздуха, Дж/(кг К);
- газовая постоянная воздуха, Дж/(кг К);
 - атмосферное давление на уровне половины высоты помещения, Па.
- атмосферное давление на уровне половины высоты помещения, Па.
В общем случае система обыкновенных дифференциальных уравнений пожара является жёсткой и решается численными методами с использованием ЭВМ. Для интегрирования системы уравнений пожара с заданными начальными условиями используется процедура Рунге-Кутта.
Прогнозирование опасных факторов пожара в помещении проводится с использованием программы INTMODEL, разработанной на кафедре «Инженерной теплофизики и гидравлики» Академии ГПС МЧС России. В программе использован метод Рунге-Кутта-Фельберга 4-5 порядка точности с переменным шагом.

