Построение математической модели ЗЛП

 

P

 

 

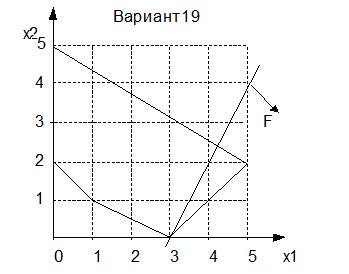
Восстанавливаем ограничения по графику:

 

AB (0,2) (0,5) x1 = 0

 

BC (0,5) (5,2)

 

              -3x1 = 5x2 -25

 

Для определения знака неравенства, возьмем точку внутри области (2;2).

Получим, -6  -15 следовательно: -3x1 - 5x2 + 25  0

 

CD (5,2) (3,0)       

 

                    -2x1 + 10 = -2x2 + 4

 

Для определения знака неравенства, возьмем точку внутри области (2;2).

Получим, 6  0 следовательно: -2x1 + 2x2 + 6  0

 

DE (3,0) (1,1)

 

                    x1 – 3 = - 2x2

Для определения знака неравенства, возьмем точку внутри области (2;2).

Получим, - 1  - 4 следовательно: x1 + 2x2 – 3  0

 

EA (1,1) (0,2)

 

                    x1 – 1 = - x2 +1

 

Для определения знака неравенства, возьмем точку внутри области (2;2).

Получим, 1  - 1 следовательно: x1 + x2 – 2  0

 

Получим уравнение целевой функции:

ЦФ (4,2)(3,0)

-2x1 + 8 = - x2 + 2

F = - 2x1 + x2 = - 6

Делаем вывод, что целевая функция принадлежит к семейству прямых, которые описываются уравнением: F = - 2x1 + x2

Для определения того, что надо искать минимум или максимум строим градиент функции (то есть берем частные производные по х₁, х₂):

Так как направление градиента противоположено с направлением, указанным стрелкой, то это значит, что мы должны двигаться в сторону, противоположную градиента функции,  а значит, мы должны искать минимум функции, то есть

Запишем ограничения в виде системы неравенств:

F = - 2x1 + x2 à min

-3x1 - 5x2 + 25  0

-2x1 + 2x2 + 6  0

x1 + 2x2 – 3  0

x1 + x2 – 2  0

 

F = - 2x1 + x2 à min

 

1.2. Решение ЗЛП графическим методом:

F(A) = 2            F(D) = -6

F(B) = 5 à max                 F(E) = -1

F(C) = -8

 

Находим оптимальное решение графически: двигаемся по направлению градиента, пока не выйдем из области, ограниченной неравенствами (симплекса). Оптимальное решение: (5;2),  F (5,2) = -2 * 5 + 2 = - 8

Значение целевой функции: - 8.
1.3. Решение ЗЛП алгебраическим методом:

Ограничения – неравенства                         Ограничения – равенства

-3x1 - 5x2 + 25  0                             - 3x1 – 5x2 + 25 =  x3

-2x1 + 2x2 + 6  0                                        - 2x1 + 2x2 + 6 = x4

x1 + 2x2 – 3  0                                        x1 + 2x2 –  3 = x5                        x1 + x2 – 2  0                                 x1 +  x2 –   2  = x6

xi  0

F = - 2x1 + x2 à min                                         Свободные х₁, х₂

    < 0, 0, 25, 6,- 3, - 2 >                                          

         

 Недопустимое решение, так как не выполнятся условие   неотрицательности для х5 (не может быть   выбрано в качестве опорного).

F = - 2x1 + x2 à min                                             

Для приведения данного решения к допустимому выведем переменную x5 из базиса и заменим её на x1.

Заменим x1 на x3

x1 = x5 -2x2 +3

Свободные х₂ ,х₅

x3 = -3x5 + 6x2 – 5x2 - 9 + 25

x4= -2(x5 – 2x2 + 3) + x2 + 6

x1 = x5 – 2x2 + 3

x6 =  x5 – 2x2 + 3 + x2 – 2

x3 = -3x5 + x2 +16  à 16/3

x4= - 2x5 + 6x2    à 0

x1 = x5 – 2x2 + 3   à ∞   (1)

x6 = x5 – x2 + 1 à ∞

 

F = -2(x5 – 2x2 + 3) + x2 = - 2x5 + 4x2 – 6 + x2 = - 2x5 + 5x2 – 6

< 3, 0, 16, 0, 0, 1 >

Допустимое (1) , может быть опорным

 

F = - 2x5 + 5x2 – 6 à min

Решение не является оптимальным, так как коэффициент при х₅ отрицателен. Переведём переменную х₅ в свободные. Заменим х₅ на х₄

x5 =1/2  x4 + 3x2

Свободные х₄ ,х₂

x3 = -3(-1/2 x4 + 3x2) + x2 + 16

x5= - 1/2  x4 + 3x2

x1 = - 1/2  x4 + 3x2 – 2x2 + 3

x6 =  - 1/2  x4 + 3x2 – x2 + 1

x3 = 3/2 x4 – 8x2 + 16      à2

x5= - 1/2 x4 + 3x2     à ∞

x1 = - 1/2 x4 + x2 + 3     à ∞

x6 =  - 1/2  x4 + 2x2 + 1       à ∞

 

F = -2(- 1/2 x4 + 3x2) + 5x2 - 6= x4 – x2 – 6

< 3, 0, 16, 0, 0, 1 >

Решение не является оптимальным, так как коэффициент при х₂ отрицателен. Переведём переменную х₂ в свободные. Заменим х₂ на х₃

x2 = 3/16 x4 – 1/8 x3 + 2

Свободные х₄ ,х₂

x2 = 3/16 x4 – 1/8 x3 + 2

x5= - 1/2  x4 + 3(3/16 x4 – 1/8 x3 + 2)

x1 = - 1/2 x4 + 3/16 x4 – 1/8 x3 + 2 + 3

x6 =  - 1/2  x4 + 2(3/16 x4 – 1/8 x3 + 2) + 1

x2 =  3/16 x4 – 1/8 x3 + 2     

x5= - 1/16 x4 – 1/8 x3 + 6  

x1 = - 5/16  x4 – 1/8 x3 + 5 

x6 = - 1/2 x4 – 1/4  x2 + 5

 

F = x4 – 3/16 x4 + 1/8 x3 – 2 – 6 = 13/16 x4 + 1/8 x3 – 8

< 5, 2, 0, 0, 6, 5 >

F =13/16 x4 + 1/8 x3 – 8 – все коэффициенты положительны, решение оптимальное в точке (5;2), значение исходной целевой функции  - 8.

1.4. Решение ЗЛП симплекс – методом:

Для решения симплекс методом воспользуемся опорным решением (1), полученным ранее.

x3 = -3x5 + x2 +16      

x4= - 2x5 + 6x2    

x1 = x5 – 2x2 + 3       (1)

x6 = x5 – x2 + 1      

 

F = - 2x5 + 5x2 – 6 à min

Преобразуем систему для решения симплекс – методом

x3 = 16 - (3x5 - x2)      

x4= 0  - (2x5 - 6x2)  

x1 = 3  - (-x5 + 2x2)       (1)

x6 = 1  - (-x5 + x2)   

 

F = - 6 – ( 2x5 – 5x2) à min

Таблица 1. Симплекс – таблица

 

Б\Св	β		x5		x2
x3	16	0	3	-3/2	-1	9
x4	0	0	2	1/2	-6	-3
x1	3	0	-1	1/2	2	-3
x6	1	0	-1	1/2	1	-3
F	-6	0	2	-1	-5	6

 

 

Так как коэффициент в целевой функции при х₅ положителен, то выбираем в качестве генерального столбца столбец х₅. В качестве генеральной строки выбираем ту строку, в которой отношение постоянной величины  к соответствующему элементу генерального столбца будет минимальным и неотрицательным.

16/3 –допустимое значение, но не минимальное

0 – допустимое, минимальное  

 -3 – недопустимое значение (отрицательное)

- 1 – недопустимое значение (отрицательное)

Минимальным из допустимых значений является значение, соответствующее 0 поэтому генеральным элементом является элемент а₂₂ (соответствует сроке х₄), тогда соответственно λ = 1/ а₂₂ = 1/2. На основании этого производим вычисления.

После вычисление получаем:

Таблица2.

Б\Св	β		x4		x2
x3	16	2	-3/2	-3/16	8	1/8
x5	0	6	1/2	-9/16	-3	3/8
x1	3	2	1/2	-3/16	-1	1/8
x6	1	4	1/2	-3/8	-2	1/4
F	-6	-2	-1	3/16	1	-1/8

 

Так как коэффициент в целевой функции при х₂ положителен, то выбираем в качестве генерального столбца столбец х₂. В качестве генеральной строки выбираем ту строку, в которой отношение постоянной величины  к соответствующему элементу генерального столбца будет минимальным и неотрицательным.

2– допустимое, минимальное  

0 – допустимое, но коэффициент x5  - отрицательный    

 -3 – недопустимое значение (отрицательное)

-1 – недопустимое значение (отрицательное)

Минимальным из допустимых значений является значение, соответствующее 2 поэтому генеральным элементом является элемент а₂₃ (соответствует сроке х₅), тогда соответственно λ = 1/ а₁₃ = 1/8. На основании этого производим вычисления.

После вычисление получаем:

Таблица3.

Б\Св	β	x4	x3
x2	2	-3/16	1/8
x5	6	1/16	3/8
x1	5	5/16	1/8
x6	5	1/2	1/4
F	-8	-13/16	-1/8

 

Так как все коэффициенты целевой функции  отрицательны, то решение оптимальное и в точке (5;2). Значение целевой функции – 8 .

< 5, 2, 0, 0, 6, 5>

В результате получили решение, аналогичное решению, получен­ному при использовании алгебраического метода, из чего делаем вывод о правильности полученного решения.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться: