Алгоритм расчета функции синуса
В данной работе используется арифметика c фиксированной запятой, следовательно, требуется, чтобы все числа были представлены по абсолютному значению меньше единицы.
Для преставления функции синуса воспользуемся формулами приведения и двойного угла:
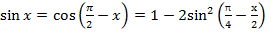(1)
для случая, когда аргумент лежит в интервале 
и
(2)
для случая, когда аргумент лежит в интервале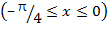 
.
Рассмотрение двух случаев обусловлено тем, что невозможно использовать лишь одно соотношение (1), так как при расчетах будут возникать числа большие единицы.
В итоговых формулах расчета функции синуса (1) и (2) присутствует умножение на 2, которое будет заменено на сложение величины самой с собой.
Таким образом, число, поступающее на вход нашей машины, не будет превышать единицы по модулю, так как максимально возможный аргумент равен 
, либо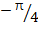 
.
Для представления формул (1) и (2) в виде общего ряда используем стандартный ряд Тейлора для синуса в диапазоне 
≤ x ≤ 
:
Для аргумента синуса равного 
разложение в ряд Тейлора будет иметь следующий вид:
Далее, общий ряд для вычисления функции sin(x) по формуле (1):
(3)
Разложение в ряд Тейлора для аргумента синуса, равного 
, будет иметь следующий вид:
И общий ряд для вычисления sin(x) по формуле (2):
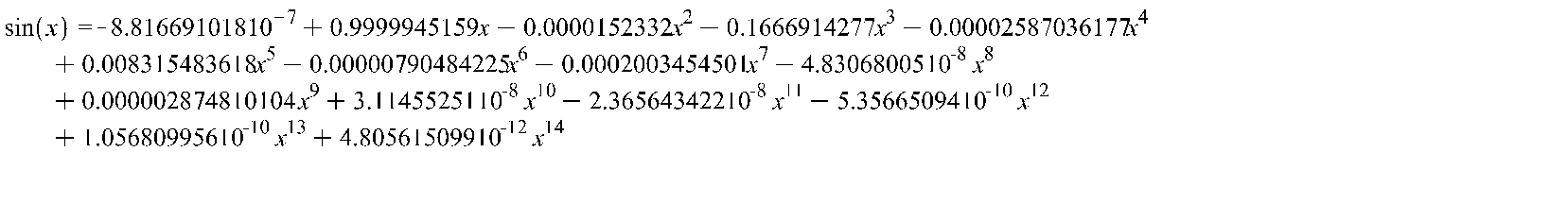
(4)
Будем рассматривать два случая:
1. В вычислительной машине реализована функция умножения. Алгоритм вычисления показан на Схеме 2.
2. В вычислительной машине не реализована функция умножения. При этом алгоритм процедуры умножения реализован отдельно и показан на Схеме 1. Алгоритм вычисления показан на Схеме 3.
| Сдвиг res на 1 разряд вправо
|
| Сдвиг res на 1 разряд вправо
|
| Схема 1. Блок-схема процедуры умножения
|
| Схема 2. Функция умножения в вычислительной машине реализована
|
| Схема 2. Функция умножения в вычислительной машине реализована
|
| Схема 3. Функция умножения в вычислительной машине не реализована
|
Оценка погрешностей
