
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Правильний знак суми визначається автоматично в процесі додавання цифр знакових розрядів операндів (і одиниці перенесення з цифрової частини, якщо вона має місце).
Характерною особливістю оберненого кода є наявність циклічного перенесення (якщо він виникає) із знакового розряду в молодший розряд цифрової частини, завдяки чому виконується корекція результату на Загальні правила додавання двійкових операндів, представлених у формі з фіксованою комою (правильні дроби), в оберненому коді можна розглянути на підставі застосування доповнення до двох і доповнення до одиниці (див. розділ 3). Розгляд будемо вести для двох основних варіантів: а) Обчислимо цей вираз із застосуванням доповнень. Як відомо, для правильних двійкових дробів
Тоді,
де Розглянемо такі три випадки: 1) Якщо Це означає, що не виникає перенесення до знакового розряду, а, також, із знакового розряду в молодший розряд результату (циклічного перенесення). Результат операції є від'ємний і записується в оберненому коді так:
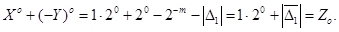 4. 4.
2) Якщо Це означає, що виникає перенесення до знакового розряду, а, також, із знакового розряду в молодший розряд результату. Додаючи перенесення із знакового розряду до отриманого результату з вагою
3) Якщо
б) Обчислимо в оберненому коді:
Вираз
де Це означає, що виникає перенесення до знакового розряду, а, також, із знакового розряду. Додаючи перенесення із знакового розряду до отриманого результату з вагою
Отримані результати дають право зформулювати таке правило додавання двох чисел в оберненому коді: Сума двох чисел в оберненому коді дорівнює сумі їх обернених кодів з урахуванням знакових розрядів. У випадку виникнення перенесення із
Наступні приклади ілюструють чотири основні варіанти додавання чисел у оберненому коді при виконанні умови 1) Приклад 1.
У звязку з тим, що обернений код додатніх чисел співпадє з записом самих чисел, оприманий результат співпадає з результатом додавання цих чисел у прямому коді. 2)
Виникає перенесення в знаковий розряд і із знакового розряду. Необхідно провести корекцію результату. 3) Приклад 3.

Сума від'ємна. Перенесення до знакового розряду немає. Корекція не потрібна. 4) Приклад 4.
Сума від'ємна. Виникає перенесення в знаковий розряд і із знакового розряду. Необхідно провести корекцію результату. Очевидно, що у всіх розглянутих випадках додавання операнди можна поміняти місцями, і при цьому результат не зміниться. Таким чином, обернений код досить зручний для виконання операцій алгебраїчного додавання, якщо врахувати простоту переведення від'ємних чисел із прямого кода в обернений і навпаки[4].
|
Последнее изменение этой страницы: 2019-06-08; Просмотров: 202; Нарушение авторского права страницы