
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Расчёт нагрузок корпусов выпарной установки по методу проф. И.А. Тищенко
Теплоёмкость дрожжевой суспензии в зависимости от концентрации а.с.в. [1] в узком интервале концентраций изменяется практически линейно. С учётом этого из уравнения теплового баланса получаем
выпаренной за счёт 1 кг первичного пара;
воды, выпаренной за счёт тепла самоиспарения раствора;
в окружающую среду. В общем методе расчёта, предложенном проф. А.И. Тищенко, принимается В соответствии с приведённым выше уравнением (12) для первого корпуса получим:
Для второго корпуса –
Суммируя уравнения (13) и (14) получим
откуда находим расход греющего пара на первый корпус установки
Теплосодержание потоков пара и жидкости определяем по паровым таблицам в зависимости от давления (таблица 1).
Таблица 1- Теплосодержание паров и конденсата по корпусам, кДж/кг
Теплоёмкость дрожжевой суспензии определяем графически в зависимости от концентрации а.с.в.
Тепловой баланс установки
По левой части уравнения (4*) определяем приход тепла
По правой части того же уравнения определяем расход тепла
Так как
Расчёт коэффициентов теплоотдачи и теплопередачи
В выпарном аппарате тепло передаётся от теплоносителя через стенку к кипящей жидкости. Передача тепла подчиняется общеизвестному уравнению
где Q – количество переданного тепла, Вт; F – поверхность теплообмена, м2; К – коэффициент теплопередачи, Вт/(м2*оС);
Коэффициент теплопередачи К рассчитывается по следующей формуле:
где
Коэффициенты теплоотдачи рассчитываются по критериальным уравнениям, в которые входят следующие критерии подобия:
перехода тепла на границе поток – стенка;
теплоносителя;
инерции и трения в потоке;
тяжести и трения;
при свободной конвекции;
агрегатного состояния теплоносителя. Критерии подобия включают величины, которые входят в условия однозначности и имеют следующие параметры:
с - удельная теплоемкость, кДж/(кг*оС); g – ускорение свободного падения, м2/с; w – скорость потока, м/с2; l – определяющий геометрический размер, м;
критерии конденсации и
Теплоотдача от конденсирующегося пара осуществляется, как правило в условиях плёночной конденсации [3, 11]. Коэффициент теплоотдачи
Скрытая теплота конденсации определяется при
Таблица 2 - Физические параметры конденсата Параметр | 1-й корпус | 2-й корпус | |||||||||||||||
| tконд, оС | 109, 5 | 109, 5 | |||||||||||||||
| tпл, оС | 106, 4 | 102, 4 | |||||||||||||||
| Скрытая теплота конденсации r, кДж/кг | 2249, 4 | 2248 | |||||||||||||||
| Динамическая вязкость, 106Па*с | 265, 4 | 275, 8 | |||||||||||||||
| Кинематическая вязкость, 106*м2/с | 0, 278 | 0, 288 | |||||||||||||||
| Теплоёмкость, кДж/(кг*оС) | 4, 23 | 4, 23 | |||||||||||||||
| Плотность, кг/м3 | 953, 5 | 956, 3 | |||||||||||||||
| Коэффициент теплопроводности среды, 102*Вт/(м*оС) | 68, 43 | 68, 35 |
Рассчитываем критерии подобия и коэффициенты теплоотдачи от пара к стенке по корпусам:
- для первого корпуса


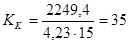
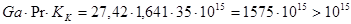 ,
,
следовательно, критерий Нуссельта рассчитываем по уравнению
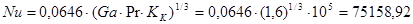
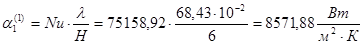 (19)
(19)
- для второго корпуса

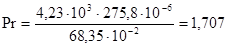
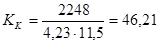
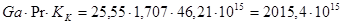
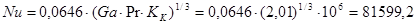
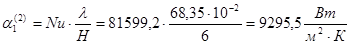
Уравнение для расчёта коэффициента теплоотдачи от стенки к суспензии выбирают в зависимости от режима движения суспензии. Для этого случая рекомендовано следующее расчётное уравнение [6, 11]:
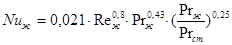 (20)
(20)
Скорость движения суспензии в трубах принимаем равной w=2, 5м/с [8].
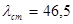 Вт/(м2* оС).
Вт/(м2* оС).
Таблица 3 - Физические параметры суспензии по корпусам
Параметр
1-й корпус
2-й корпус
Температура, оС
97
83
Теплоёмкость, кДж/(кг*оС)
3, 55
3, 47
Динамическая вязкость, Па*с
2, 3*10-3
2, 2*10-3
Коэффициент теплопроводности среды, 102*Вт/(м*оС)
64, 3
62, 0
Определяющим геометрическим размером при определении Re и Nu является внутренний диаметр кипятильных труб d = 0, 034 м [1].
Рассчитываем критерии подобия и коэффициенты 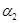 по корпусам:
по корпусам:
- для первого корпуса
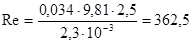
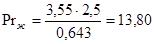

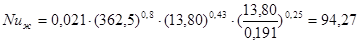
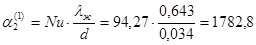
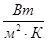
- для второго корпуса
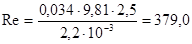
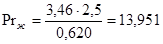
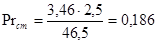
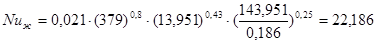
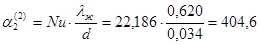
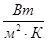
Значения 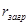 определяем по [8, с. 531]:
определяем по [8, с. 531]:
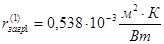
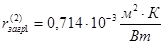
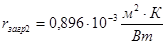 (как для сырых нефтепродуктов).
(как для сырых нефтепродуктов).
Отсюда находим коэффициенты теплопередачи Кi по корпусам:
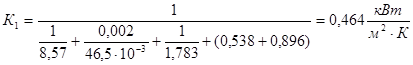
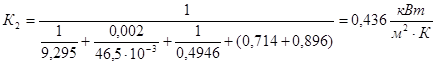
Последнее изменение этой страницы: 2020-02-16; Просмотров: 122; Нарушение авторского права страницы