
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МОДЕЛИ ⇐ ПредыдущаяСтр 2 из 2
Построим граф модели СПО:
S 1 – СМО моделирует П-ОП S 2 - СМО моделирует НМД S3 - СМО моделирует СК К параметрам модели относятся следующие величины: Число N систем массового обслуживания. Из приведенной выше схемы модели СПО следует, что N=3. Число каналов, входящих в каждую СМО. В нашей модели все СМО являются одноканальными, следовательно:
3. Матрица вероятностей передач P =| где
Подсчитаем вероятности переходов системы. Очевидно, что: Чтобы найти вероятности остальных передач, найдем суммарное число обращений к файлам Q: Тогда:
Так как:
То: 4. Число М заявок, циркулирующих в замкнутой сети: M=1, 3, 5. 5. Средние длительности обслуживания заявок Для расчета некоторых
где: n – число файлов;  - число обращений к файлу - число обращений к файлу 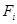 ; ;  - средняя длина записи файла - средняя длина записи файла 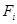 ; ;  -быстродействие устройства, в нашем случае -быстродействие устройства, в нашем случае  = = 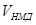 . .
РАСЧЕТ ХАРАКТЕРИСТИК МОДЕЛИ Расчет характеристик для М=1. 1. Определим значения коэффициентов передач
Коэффициент передачи
Как видим, значение
Теперь можно определить время обслуживания заявки в процессоре. Оно определяется как среднее арифметическое от времени обслуживания заявки в каждой из СМО с учетом коэффициентов передач: 2. Определение вероятности состояний Вероятности состояний замкнутой сети определяются следующим выражением:
где:
Здесь Ki – число каналов (приборов) в i-й системе. Символ
Перечислим эти состояния: (1, 0, 0), (0, 1, 0), (0, 0, 1).
Для вычисления вероятностей возможных состояний нам в дальнейшем потребуются значения произведений
Теперь отдельно вычислим знаменатель выражения (1):
Тогда:
3. Определение коэффициентов загрузки Для М=1 имеем, что
4. Определение интенсивности Интенсивность входного потока – это число заявок, поступающих в единицу времени на вход соответствующей СМО. Общая формула для расчета: Найдем Остальные
Определение времени цикла замкнутой сети. Время цикла относительно i – ого узла – это среднее время от момента входа (выхода) одной и той же заявки в этот i – ый узел. Общая формула:
Определим время цикла для нулевой системы:
6. Определение среднего числа заявок mi в каждой СМО. Общая формула для расчета:
Расчет характеристик для М=3. 1. Определение вероятности состояний
Число заявок в системе M=3, число СМО N=3, тогда число возможных состояний найдем как: Перечислим эти состояния: (3, 0, 0), (2, 1, 0), (2, 0, 1), (1, 2, 0), (1, 1, 1), (1, 0, 2), (0, 3, 0), (0, 2, 1), (0, 1, 2), (0, 0, 3).
Теперь отдельно вычислим знаменатель выражения (1):
Вероятности всех состояний представим в виде таблицы, опустив множество формул их определения:
2. Определение коэффициентов загрузки Коэффициент загрузки здесь удобнее определять через коэффициент простоя. Коэффициент простоя hi для каждой из одноканальных систем сети вычисляется суммированием по всем разложениям М вероятностей (1), для которых mi =0, т.е. суммированием всех вероятностей простоя i-й системы:
Тогда по формуле:
3. Определение интенсивности Общая формула для расчета: Найдем Остальные
|
Последнее изменение этой страницы: 2020-02-16; Просмотров: 117; Нарушение авторского права страницы