Закон распределения Стьюдента.

Закон назван псевдонимом В.С. Госсета. Закон применяется при обработке небольшого числа (от 2 до 20) многократных измерений, погрешности которых подчинены нормальному закону распределения.

Закон распределения Стьюдента описывает распределение плотности вероятности 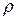 значений случайной величины  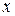как функцию относительного аргумента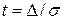

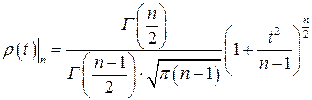,                 (1.16)

где 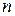- число повторных измерений.

Распределение Стьюднта приближается к нормированному нормальному распределению с увеличением числа повторных измерений.

Для определения вероятности 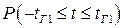 при законе распределения Стьюдента необходимо вычислить интеграл

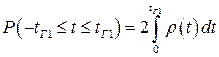.                         (1.17)

Предел интегрирования 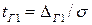 называется коэффициентом Стьюдента. При расчете коэффициента Стьюдента задаются доверительной вероятностью  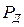и числом повторных наблюдений n, поэтому коэффициент Стьюдента обозначают  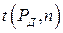или просто t. Значения коэффициентов Стьюдента приведены в таблице 1.2

 

Таблица 1.2. Значения коэффициентов Стьюдента

 

n -1
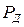
	0.90	0.95	0.98	0.99	0.999
1	6.31	12.7	31.8	63.7	636.
2	2.92	4.30	6.96	9.92	31.6
3	2.35	3.18	4.54	5.84	12.9
4	2.13	2.78	3.75	4.60	8.61
5	2.02	2.57	3.36	4.03	6.87
6	1.94	2.45	3.14	3.71	5.96
7	1.90	2.36	3.00	3.50	5.41
8	1.86	2.31	2.90	3.36	5.04
9	1.83	2.26	2.82	3.25	4.78
10	1.81	2.23	2.76	3.17	4.59
12	1.78	2.18	2.68	3.05	4.32
14	1.76	2.14	2.62	2.99	4.14
16	1.74	2.12	2.58	2.95	4.02
18	1.73	2.10	2.55	2.88	3.92
20	1.72	2.09	2.53	2.85	3.85

 

На основе распределения Стьюдента разработан критерий отбора ошибочных результатов измерений. Согласно критерия Стьюдента считаются ошибочными измерения, удовлетворяющие условию

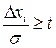,                                            (1.18)

где 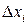 погрешность i – го измерения; t – коэффициент Стьюдента при заданной вероятности P и числе повторных измерений n. Критерий Стьюдента отсеивает с надежностью P такие результаты измерений, которые не попадают в доверительный интервал 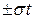, при этом надежность P определяется вероятностью P получения точного результата и зависит от погрешности измерительного прибора.

 

  1. 2.4. Обработка результатов прямых измерений

 

Целью обработки результатов прямых измерений является определение среднего арифметического значения 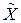 измеряемой физической величины как наиболее близкого к истинному значению, отклонение  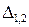среднего арифметического от истинного значения с вероятностью 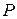, а также выявление конкретного вида закона распределения плотности вероятностей  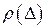случайной погрешности .

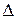Для определения среднего арифметического значения 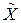 измеряемой физической величины необходимо выполнить  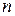равноточных измерений физической величины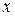

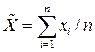.                               (1.19)

Среднее арифметическое значение 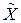 фактически является оценкой измеряемой физической величины 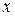. Затем вычисляется абсолютная погрешность каждого из  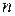измерений.

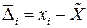.                                 (1.20)

Далее по известной в теории вероятностей формуле находится оценка среднеквадратического отклонения 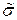 измерений, характеризующая точность метода измерений

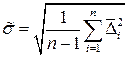.                                  (1.21)

Т.к. среднее арифметическое само обладает случайной погрешностью, то вводится понятие оценки среднеквадратического отклонения среднего арифметического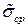

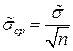.                                      (1.22)

Видно, что с увеличением числа измерений одной и той же физической величины точность оценки среднего арифметического увеличивается.

Оценка среднеквадратического отклонения среднего арифметического 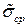 указывает на границы интервала, в котором может находиться истинное значение физической величины. В зависимости от класса точности измерительного прибора определяется доверительная вероятность 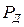. Затем в зависимости от числа n измерений физической величины задается значение интеграла вероятностей  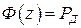(при ) или вероятность 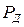 в законе распределения Стьюдента (при 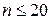). По таблицам 2.1 или 2.2, определяется  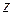или 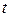, а затем вычисляется доверительный интервал  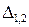отклонения от истинной оценки среднего арифметического значения измеряемой величины  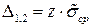или 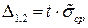 с вероятностью .

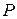Таким образом, истинное значение измеряемой физической величины 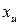 находится между нижней  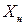и верхней  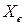границами

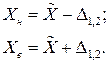                                       (1.23)

Результат измерений записывается в виде

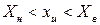 с вероятностью 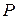.                  (1.24)

Обработка результатов прямых измерений ставит своей целью выявление конкретного вида закона распределения плотности вероятностей случайной погрешности. Для этого производятся многократные измерения одной и той же физической величины 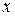. Полученные значения 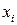, где , содержат погрешности 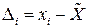. Полученный массив погрешностей используется для построения экспериментальной зависимости 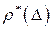. 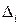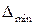Для ее построения весь диапазон значений погрешности  от  до 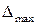 делится на одинаковые интервалы, число которых N  находится по правилу Старджесса

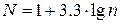.                                    (1.25)

Ширина каждого интервала 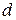 вычисляется в соответствии с выражением

.                                    (1.26)

Затем находится число значений 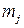, где 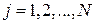, случайной погрешности 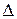, приходящихся на каждый j – й интервал, причем

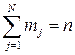.                                   (1.27)

Вероятность попадания погрешности 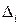 в j – й интервал определяется как доля значений  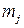в общем числе значений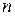

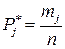.                                     (1.28)

Распределение плотности вероятностей случайной погрешности 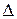 в пределах каждого  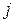- го интервала постоянна и равна

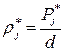.                                       (1.29)

Строится гистограмма – ступенчатая характеристика с уровнями 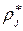 на каждом интервале d, отвечающая условию

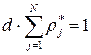.                                (1.30)

Пример гистограммы приведен на рисунке 1.6

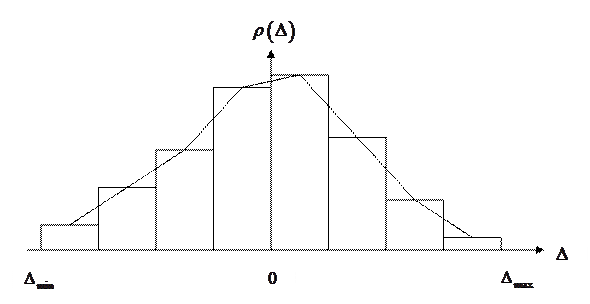
Рис. 1.6. Гистограмма

 

На основе гистограммы строится практическая зависимость распределения плотности вероятностей 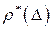, которая называется полигоном. Для ее построения соединяют отрезками прямых середины верхних сторон всех прямоугольников гистограммы.

Теоретическая зависимость 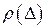, наилучшим образом описывающая практическую зависимость распределения плотности вероятностей  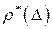ищется подбором некоторой аналитической функции 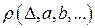, где 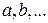- постоянные коэффициенты, определяемые в соответствии с методом моментов. Суть метода моментов заключается в том, чтобы основные характеристики теоретического и практического законов распределения плотности вероятностей совпадали. Вместе с тем теоретическая зависимость должна удовлетворять основным свойствам законов распределения

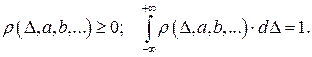                 (1.31)

Если в качестве теоретической зависимости выбран нормальный закон распределения плотности вероятностей, то центр распределения должен быть равен 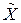 и среднеквадратическое отклонение  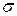погрешности  должно быть равно оценке 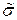 среднеквадратического отклонения измерений. Таким образом, выражение для теоретического закона распределения плотности вероятностей примет вид

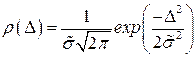.                              (1.32)

Однако теоретический закон распределения от практического может существенно отличаться. Для оценки степени соответствия этих законов применяют критерий согласия Пирсона (χ ² - «хи-квадрат»). С этой целью вычисляют

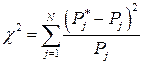,                          (1.33)

где 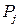 - вероятность попадания погрешности  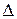в 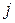-й интервал в теоретическом законе распределения.

Вероятность 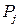 можно вычислить по формуле

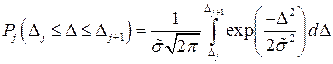             (1.34)

где 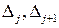- границы  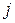-го интервала, или приближенно по формуле

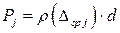,                                     (1.35)

    где 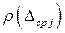 - значение теоретического закона распределения, вычисляемое по формуле (1.32), в точке 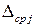, причем

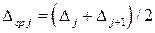.                                    (1.36)

Чем меньше χ ², тем ближе теоретический закон распределения к практическому. Граничные значения 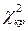, по которым можно судить о соответствии теоретического закона распределения практическому, приведены в таблице 1.3.

Граничное значение 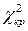 как функцию параметров  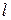и 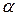 выбирают из приведенной таблицы 1.3, где  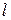- число степеней свободы, определяемое из выражения 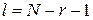;  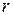- количество числовых параметров теоретического закона, оцененных по результатам измерений;  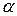- уровень значимости, численно равный вероятности признания практического закона распределения не соответствующего теоретическому.

 

 

Таблица 1.3. Таблица критических значений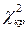

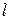
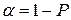
	0.01	0.05	0.10	0.50
2	0.020	0.103	0.211	1.386
3	0.115	0.352	0.584	2.366
4	0.297	0.711	1.064	3.357
5	0.554	1.145	1.610	4.351
6	0.872	1.635	2.204	5.348
7	1.239	2.167	2.833	6.346

 

Для нормального закона распределения принимают: 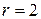;  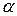- минимальное. Расчетное значение χ ² сравнивают с граничным 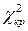. Если выполняется условие

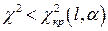,                         (1.37)

то гипотезу о соответствии практического закона распределения теоретическому принимают за истину. В противном случае считают гипотезу не соответствующей действительности и строят новую, которая также проверяется.

 

 1. 2. 5. Обработка результатов косвенных измерений

При косвенных измерениях искомая величина 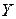 является функцией ряда других величин - аргументов .

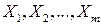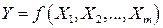.                                    (1.38)

Результат косвенных измерений оценивается погрешностью 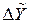, которая определяется погрешностями аргументов 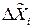, где 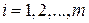, и наличием статистической связи (корреляции) между аргументами.

Представим погрешности аргументов 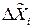 в виде систематической  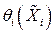и случайной  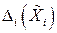составляющих

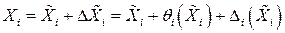.                     (1.39)

Тогда результат косвенных измерений можно представить через погрешности аргументов

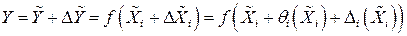.      (1.40)

Разложим функцию 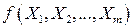 в ряд Тейлора, отбросим отклонения выше первого порядка и выразим результат через среднеарифметические значения и погрешности аргументов

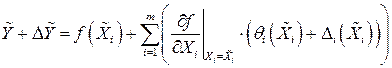,         (1.41)

где 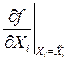- коэффициент влияния i – го аргумента;

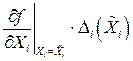   - частная погрешность i – го аргумента.

Из формулы (1.41) получаем выражение для оценки результата косвенного измерения

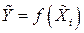,                                                    (1.42)

а также выражения для оценки систематической 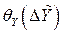 и случайной  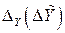погрешностей результата косвенного измерения

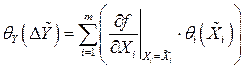;                   (1.43)

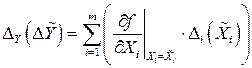.                   (1.44)

 

Из выражения (1.44) можно найти приближенное выражение для оценки среднеквадратического отклонения 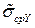 случайной погрешности результата косвенного измерения в зависимости от оценок среднеквадратических отклонений  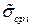случайных погрешностей аргументов

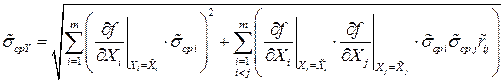,   (1.45)

где 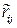 - оценка коэффициента корреляции, определяющая меру статистической связи случайных величин  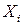и .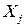

Все возможные оценки коэффициента корреляции  лежат в интервале от -1 до +1. Установить значение 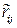 обычно затруднено, поэтому рассматривают два случая:  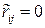(отсутствие статистической связи) и  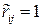(полная статистическая связь).

При 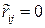 формула (2.45) преобразуется к виду

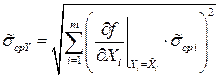,                     (1.46)

т.е. оценки среднеквадратических отклонений 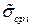 случайных погрешностей аргументов суммируются геометрически как независимые случайные.

При 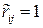 формула (2.45) преобразуется к виду

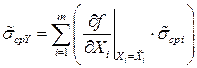,                              (1.47)

т.е. оценки среднеквадратических отклонений 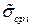 случайных погрешностей аргументов суммируются алгебраически с учетом знаков.

    Результат косвенных измерений записывается в соответствии с выражением (1.24), т.е. также как и при прямых измерениях, но доверительный интервал 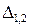  вычисляется с учетом оценок среднеквадратических отклонений  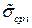случайных погрешностей аргументов и оценок коэффициентов корреляции  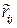между ними.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться: