
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Расчет числовых характеристик распределения случайных величин ⇐ ПредыдущаяСтр 8 из 8
Более полное, а главное, обобщенное представление о результатах эксперимента дают не абсолютные, а относительные (удельные) значения полученных данных. Так, вместо абсолютных значений числа экспериментальных данных ni, целесообразно подсчитать долю рассматриваемых событий в интервале, приходящихся на одно изделие (деталь, узел, агрегат или автомобиль) из числа находящихся под наблюдением, т.е. на единицу выборки. Эта характеристика экспериментального распределения называется относительной частотой (частостью) mi появления данного события (значений признака Xi):
Относительная частота mi при этом, в соответствии с законом больших чисел, является приближенной экспериментальной оценкой вероятности появления события Значения экспериментальных точек интегральной функции распределения
и т.д., т.е.
Таким образом, значение Другим удельным показателем экспериментального распределения является дифференциальная функция
и характеризующая долю рассматриваемых событий в интервале, приходящуюся на одно испытываемое изделие и на величину ширины интервала. Функция Полученные результаты расчета сводим в статистическую таблицу. Таблица 2 Результаты интервальной обработки экспериментальных данных.
Анализ физических закономерностей формирования распределения случайных величин по значениям исследуемого показателя
Распределение Вейбулла. Данное распределение проявляется в модели “слабого звена”, т.е. если система состоит, из которых приводит к отказу всей системы. Распределение времени до отказа, наработки до отказа хорошо описывается распределением Вейбулла. Многие изделия (агрегаты, узлы, системы автомобиля) при анализе модели отказа могут быть рассмотрены как состояния из нескольких элементов (участков), разрушение которых происходит при разной наработке, однако ресурс изделия в целом определяется наиболее слабым его участком. Распределение Вейбулла - очень гибкий закон для оценки показателей надежности автомобилей. В решении задач ТЭА Vx=0.35…0.8. Закон Вейбулла хорошо описывает процессы, где на отказ действуют причины износа и усталости. Математическая модель распределения Вейбулла задается двумя параметрами, что обуславливает широкий диапазон его применения на практике. Дифференциальная функция имеет вид:
где
Интегральная функция имеет вид:
Расчет параметров математических моделей Распределение Вейбулла Распределение Вейбулла - очень гибкий закон для оценки показателей надежности автомобилей. В решении задач ТЭА Vx=0.35…0.8. Закон Вейбулла хорошо описывает процессы, где на отказ действуют причины износа и усталости. Математическая модель распределения Вейбулла задается двумя параметрами, что обуславливает широкий диапазон его применения на практике. Дифференциальная функция имеет вид:
где
Интегральная функция имеет вид:
Заготавливаем статистическую таблицу Таблица 2.4
Номер интервала | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.Границы интервалов | 15 | 30 | 45 | 60 | 75 | 90 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | 45 | 60 | 75 | 90 | 105 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.Середины интервалов | 22, 5 | 37, 5 | 52, 5 | 67, 5 | 82, 5 | 97, 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.Опытные числа попаданий в интервалы m | 6 | 2 | 6 | 2 | 1 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4.Опытные частоты попаданий в интервалы | 0, 333 | 0, 111 | 0, 333 | 0, 111 | 0, 056 | 0, 056 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. Вход в статистическую таблицу | 0, 4 | 0, 7 | 1 | 1, 3 | 1, 6 | 1, 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. Табличные значения функции α =f(xi) | 0, 6685 | 0, 8595 | 0, 7485 | 0, 484 | 0, 244 | 0, 0955 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. Теоретические вероятности попадания в интервалы Pi | 0, 191 | 0, 245 | 0, 213 | 0, 138 | 0, 07 | 0, 027 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. Теоретические числа попаданий в интервалы m* | 3, 438 | 4, 41 | 3, 834 | 2, 484 | 1, 26 | 0, 486 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. Слагаемые критерия Пирсона | 1, 9092 | 1, 317 | 1, 224 | 0, 094 | 0, 054 | 0, 544 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. Вероятности исправной работы | 0, 855 | 0, 615 | 0, 37 | 0, 176 | 0, 067 | 0, 027 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. Теоретическая функция распределения F(xi) | 0, 191 | 0, 436 | 0, 649 | 0, 787 | 0, 857 | 0, 884 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.Экспериментальные значения интегральной функции F(xi)э | 0, 333 | 0, 444 | 0, 777 | 0, 888 | 0, 944 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вычисляем статистическое математическое ожидание (генеральное среднее)
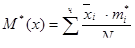
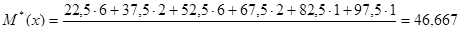

Вычисляем статистическую дисперсию
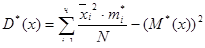
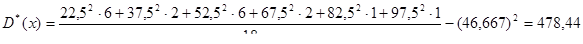
Находим несмещенное значение дисперсии
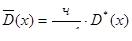
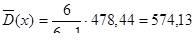
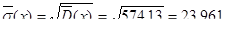
Находим коэффициент вариации
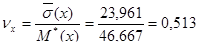
По таблицам для найденного коэффициента вариации находим значение первого параметра закона- параметра формы, равного 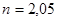
Находим второй параметр закона - параметр масштаба:
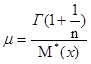
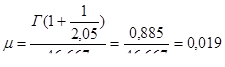
при этом значение, обратное параметру масштаба, составляет
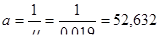
Вычисляем теоретические вероятности попаданий в интервал.
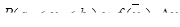
Составляем входы в статистические таблицы и определяем 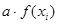
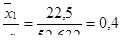
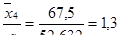
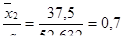
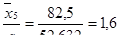
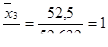
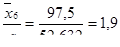
Заносим полученные входы в строку 5 табл. 2.4
С помощью полученных входов для 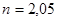 , находим (путем интерполяции) значения функции
, находим (путем интерполяции) значения функции 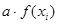
Указанные значения составляют:
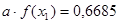
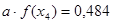
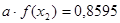
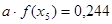
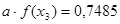
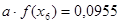
Находим дифференциальную функцию распределения:
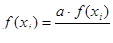
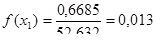
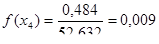
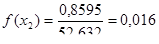
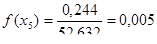
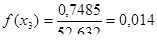
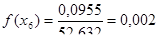
Находим теоретические вероятности попадания случайной величины в интервалы:
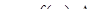
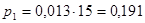
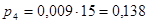
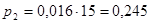



Таким образом заполняем строку 7 табл. 2.4
Вычисляем теоретические числа попадания в интервал:

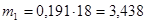
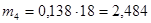
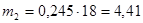
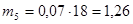


Заполняем строку 8 табл. 2.4
Вычисляем слагаемые критерия Пирсона:
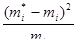
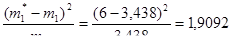
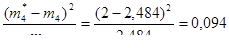
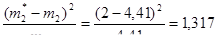
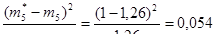
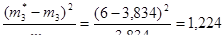
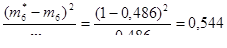
Заполняем строку 9 табл. 2.4
Суммируя слагаемые критерия Пирсона по интервалам, получаем
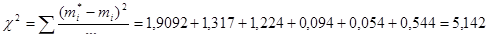
Проверяем правдоподобность принятия гипотезы о принадлежности опытных данных к закону Вейбулла.
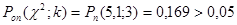
Следовательно, по критерию Пирсона при уровне значимости α =0, 05 гипотеза о принадлежности опытных данных к закону Вейбулла не отвергается.
Проверим правдоподобность по критерию Романовского:
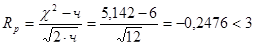 - гипотеза не отвергается.
- гипотеза не отвергается.
Расчет критерия Колмогорова.
В каждом из интервалов определяем модуль разности между экспериментальными значениями интегральной функции F(xi)э и теоретическими F(xi), т.е.
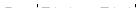
и выбираем максимальное значение Dmax. Вычисляем расчетное значение критерия:
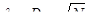
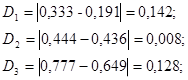
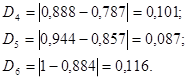
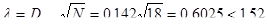
Таким образом, по критерию Колмогорова гипотеза не отвергается.
Заключение
При выполнении данной курсовой работы были просчитаны законы распределения: Вейбулла, экспоненциальный и 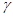 - распределение. Эти законы распределения отвергаются по всем критериям и однозначно не подходят к данному вариационному ряду.
- распределение. Эти законы распределения отвергаются по всем критериям и однозначно не подходят к данному вариационному ряду.
Выводы: В результате проделанных расчетов мы можем сделать вывод, что в нашем случае больше всего подходит нормальное распределение времени проверки состояния и крепления рулевых тяг автомобилей BMW. Мы это заключение сделали на основании рассчитанных критериев о принадлежности той или иной гипотезы. Выбранное распределение не отвергается не по одному из критериев и имеет наименьшее их значение:
- критерий Романовского: 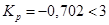
- критерий Пирсона: 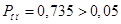
- критерий Колмогорова: 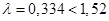
Последнее изменение этой страницы: 2020-02-17; Просмотров: 142; Нарушение авторского права страницы