
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Магнитное поле в центре кругового тока I радиусом RСтр 1 из 2Следующая ⇒
Магнитное поле Магнитное поле – это силовое поле в пространстве, окружающее токи и постоянные магниты. Таким образом, магнитное поле создается движущимися зарядами или электрическим током. Характеристикой магнитного поля является магнитная индукция. Для движущегося заряда она определяется как μ 0 = 4π ∙ 10 -7 Гн/м – магнитная постоянная; r – радиус вектор, проведенный от заряда к точке наблюдения.
Модуль магнитной индукции Вектор магнитной индукции В определяет силы, действующие на токи или движущиеся заряды в магнитном поле (характеризует магнитное поле, создаваемое всеми макро- и микротоками). Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор В направлен по касательной. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции
Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Направление линии вектора магнитной индукции также связано с направлением тока правилом правого винта (правилом буравчика): направление вращения рукоятки буравчика совпадает с направлением вектора В если при вращении буравчик перемещается в направлении тока. Магнитное поле прямолинейного проводника с током.
Закон Био-Савара-Лапласа
где Величина магнитной индукции
где a - угол между направлением тока и радиусом-вектором r. С помощью закона Био-Савара-Лапласа можно получить формулы для расчета магнитной индукции поля токов, текущих по проводникам разной конфигурации. Магнитное поле в центре кругового тока I радиусом R

Индукция магнитного поля, создаваемого частью окружности n:
где r - кратчайшее расстояние от проводника до точки, в которой определяется магнитная индукция, a1 и a2 - углы между элементами тока на концах проводника и радиус-векторами, проведенными от элементов к точке наблюдения. Магнитное поле бесконечно длинного прямого проводника с током
Принцип суперпозиции полей Если поле создано системой проводников с токами I1, I2, I3, ..., каждый из которых создает поле с индукцией В1, В2, В3, ..., то индукция результирующего поля равна векторной сумме индукций полей, создаваемых отдельными проводниками:
Наряду с В вводится векторная величина Н – напряженность, которая характеризует магнитное поле макротоков. Формула связи: В = µμ 0 Н, где µ - магнитная проницаемость среды, безразмерная величина, показывающая во сколько раз магнитное поле макротоков усиливается за счет поля микротоков среды. (Микротоки обусловлены движением электронов в атомах и молекулах. Эти микроскопические молекулярные токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле). Для воздуха или вакуума µ = 1.
Сила Лоренца Сила, действующая на движущийся заряд в магнитном поле - сила Лоренца, определяется выражением
Модуль силы Лоренца равен:
Сила Лоренца направлена перпендикулярна векторам v и B.
Движение заряженных частиц в магнитном поле
Пусть точечный заряд q влетает в магнитное поле с индукцией В. На движущийся заряд магнитное поле действует с силой Лоренца, 1. Частица влетает вдоль линий магнитной индукции
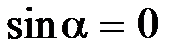 , поэтому F = 0, магнитное поле на заряд не действует. , поэтому F = 0, магнитное поле на заряд не действует.
Следовательно, заряд продолжает равномерное движение вдоль силовых линий поля со скоростью v ç ç . 2. Частица влетает поперек линий магнитной индукции Обозначим скорость, направленную перпендикулярно линиям вектора В через v ^. Угол между векторами В и v ç ç .
Поскольку тангенциальное ускорение равно нулю, величина скорости не изменяется, заряд совершает равномерное вращение. Определим период вращательного движения:
3. Частица влетает под углом к линиям магнитной индукции
Модули составляющих вектора можно выразить через угол a как Данное движение можно рассматривать как наложение двух уже описанных видов движения - равномерное перемещение вдоль линий магнитной индукции со скоростью v ç ç и равномерное вращение вокруг линий магнитной индукции со скоростью v ^. В результате заряд движется по винтовой линии.
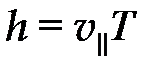 , ,
Сила Ампера Суммарная сила, действующая на все движущиеся заряды, находящиеся в участке проводника, называется силой Ампера или это сила, действующая на проводник с током. В случае прямолинейного проводника длиной l, находящемся в однородном магнитном поле, модуль силы Ампера равен
Для определения направления FА используют правило левой руки: если левую руку расположить так, чтобы силовые линии входили в ладонь, а четыре пальца указывали направление тока в проводнике, то отведенный под углом 90° большой палец определит направление силы Ампера.
Магнитный поток
где a - угол между вектором магнитной индукции В и вектором нормали n к поверхности. Поскольку проекция вектора напряженности на направление нормали равна
Если поле неоднородное или поверхность имеет произвольную форму, то поверхность, через которую требуется рассчитать поток вектора напряженности, следует разбить на бесконечно малые элементы dS. В пределах каждого элемента магнитная индукция не изменяется ни по величине, ни по направлению, т.е. поле можно считать однородным, а саму площадку – плоской.
т.е. потоком вектора магнитной индукции через поверхность S называется интеграл по поверхности от проекции вектора индукции на направление нормали. Магнитное поле Магнитное поле – это силовое поле в пространстве, окружающее токи и постоянные магниты. Таким образом, магнитное поле создается движущимися зарядами или электрическим током. Характеристикой магнитного поля является магнитная индукция. Для движущегося заряда она определяется как μ 0 = 4π ∙ 10 -7 Гн/м – магнитная постоянная; r – радиус вектор, проведенный от заряда к точке наблюдения.
Модуль магнитной индукции Вектор магнитной индукции В определяет силы, действующие на токи или движущиеся заряды в магнитном поле (характеризует магнитное поле, создаваемое всеми макро- и микротоками). Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор В направлен по касательной. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции
Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Направление линии вектора магнитной индукции также связано с направлением тока правилом правого винта (правилом буравчика): направление вращения рукоятки буравчика совпадает с направлением вектора В если при вращении буравчик перемещается в направлении тока. Магнитное поле прямолинейного проводника с током.
Закон Био-Савара-Лапласа
где Величина магнитной индукции
где a - угол между направлением тока и радиусом-вектором r. С помощью закона Био-Савара-Лапласа можно получить формулы для расчета магнитной индукции поля токов, текущих по проводникам разной конфигурации. Магнитное поле в центре кругового тока I радиусом R

Индукция магнитного поля, создаваемого частью окружности n:
где r - кратчайшее расстояние от проводника до точки, в которой определяется магнитная индукция, a1 и a2 - углы между элементами тока на концах проводника и радиус-векторами, проведенными от элементов к точке наблюдения. |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 1400; Нарушение авторского права страницы