Понятие о дифференциальных уравнениях.
Уравнения 1-го порядка с разделяющимися переменными.
5.1.Выяснить, является ли функция у=  решением дифференциального уравнения
решением дифференциального уравнения  .
.
5.2.Выяснить, является ли функция  решением дифференциального уравнения
решением дифференциального уравнения 
5.3.Является ли функция  решением дифференциального уравнения
решением дифференциального уравнения 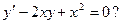
5.4.Является ли функция  решением дифференциального уравнения
решением дифференциального уравнения 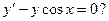
Найти общий интеграл дифференциального уравнения:

Найти частный интеграл дифференциального уравнения, удовлетворяющий указанным начальным условиям:

5.2. Линейные дифференциальные уравнения 1-го порядка.
Найти общее решение дифференциального уравнения:
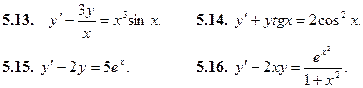
Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям:

5.3. Линейные дифференциальные уравнения 2-го порядка
с постоянными коэффициентами.
Найти общее решение дифференциального уравнения:
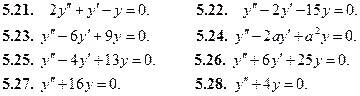
Найти общее решение дифференциального уравнения:
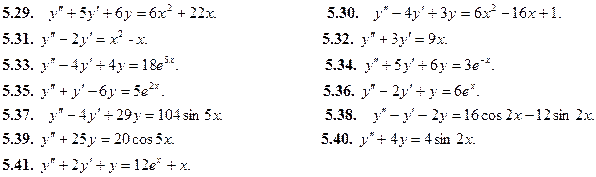
Тема 6. Ряды.
6.1.Понятие числового ряда. Необходимое условие сходимости ряда.
Ряды с неотрицательными членами. Признаки сходимости.
Вычислить первые четыре члена ряда:




Найти формулу для общего члена ряда:
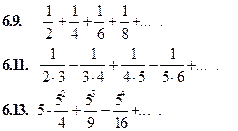
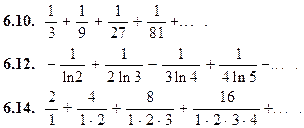
Проверить, выполнено ли необходимое условие сходимости ряда:





6.24. Выяснить вопрос о сходимости и для сходящихся рядов найти их суммы:

Сравнением с рядом  a> 0 или
a> 0 или  исследовать сходимость ряда:
исследовать сходимость ряда:







C помощью признака Даламбера исследовать, сходятся или расходятся ряды:





C помощью интегрального признака исследовать, сходятся или расходятся ряды:



6.2. Знакопеременные ряды. Абсолютная и условная сходимость ряда.
Исследовать на абсолютную и условную сходимость следующие ряды:
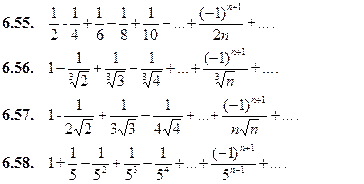

6.3. Степенные ряды. Разложение функций в степенной ряд.
Найти радиус и область сходимости ряда:


Разложить функцию в ряд Маклорена и найти интервал сходимости полученного ряда.
6.97. f(x)=  . 6.98. f(x)= ax, a> 0, a
. 6.98. f(x)= ax, a> 0, a  1.
1.
6.99. f(x)= sin 3x. 6.100. f(x)= e-5x.
6.101. f(x)= cos x2. 6.102. f(x)= 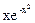 .
.
6.103. f(x)= x3 e5x. 6.104. f(x)= x2cos2x.
6.105. f(x)= sin2 x. 6.106. f(x)= cos2x.
6.107. f(x)= ln(1-x3 ). 6.108. f(x)= ln(1+3x2).
6.109. f(x)= ln(2+3x). 6.110. f(x)= ln(10-x).
6.111. f(x)= ln  . 6.112. f(x)= ln
. 6.112. f(x)= ln 
6.113. f(x)= ln(x2 +3x +2). 6.114. f(x)= ln(x2 -4x+3).
6.115. f(x)=  . 6.116. f(x)=
. 6.116. f(x)=  .
.
6.117. f(x)= 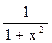 . 6.118. f(x)=
. 6.118. f(x)=  .
.
6.119. f(x)=  . 6.120. f(x)=
. 6.120. f(x)=  .
.
6.121. Пользуясь разложением функции f(x)= 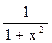 , полученным в задаче 6.117, найти разложение в ряд Маклорена для функции f(x)=arctg x.
, полученным в задаче 6.117, найти разложение в ряд Маклорена для функции f(x)=arctg x.
6.122. Пользуясь разложением функции  , при
, при  < 1, найти разложение в ряд Маклорена для функции
< 1, найти разложение в ряд Маклорена для функции
f(x)=arcsin x.
6.123.Определить в виде рядов по степеням х интегралы:

6.124. Разложить функцию:
1) f(x)=x4+x2 в ряд по степеням (х-2);
2) f(x)=x3-4x2+2x+1 в ряд по степеням (х+2);
3) f(x)=  в ряд по степеням (х-4);
в ряд по степеням (х-4);
4) f(x)=  в ряд по степеням (х-9);
в ряд по степеням (х-9);
5) f(x)=sin x в ряд по степеням (х-  ).
).
В каждом случае найти радиус сходимости ряда.
6.125. Пользуясь разложением в ряд Маклорена для функции  , полученным в задаче 6.115, вычислить:
, полученным в задаче 6.115, вычислить: 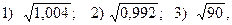 ограничившись двумя членами ряда. Оценить погрешность.
ограничившись двумя членами ряда. Оценить погрешность.
6.126.Пользуясь разложением в ряд Маклорена для функции ln  , полученным в задаче 6.111, и ограничившись тремя членами этого разложения, вычислить: 1)ln 2; 2) ln 3.
, полученным в задаче 6.111, и ограничившись тремя членами этого разложения, вычислить: 1)ln 2; 2) ln 3.
6.127. Определить в виде ряда функцию
Ф(х)=  и вычислить Ф(
и вычислить Ф(  ) с точностью до 0, 001.
) с точностью до 0, 001.
Ответы.
Тема 1.


1.81.1) непрерывна; 2) разрывна в точке х=6; 3) разрывна в точке х=0.
1.82. 1) разрывна в точке х=0; 2) разрывна в точках х=0;  ; 3) непрерывна; 4) разрывна в точке х=0; 5) разрывна в точке х=10; 6) непрерывна; 7) разрывна в точке х=-10; 8) непрерывна. 1.83. х=2 - точка разрыва II рода. 1.84. х=2 и х=3 - точки разрыва II рода. 1.85. х=1 - точка разрыва II рода.
; 3) непрерывна; 4) разрывна в точке х=0; 5) разрывна в точке х=10; 6) непрерывна; 7) разрывна в точке х=-10; 8) непрерывна. 1.83. х=2 - точка разрыва II рода. 1.84. х=2 и х=3 - точки разрыва II рода. 1.85. х=1 - точка разрыва II рода.
1.86.х=1 - точка разрыва II рода. 1.87. х=0 - точка разрыва I рода. 1.88. х=0 - точка разрыва II рода. 1.89. х=0 - точка разрыва I рода.
Тема 2.
2.1.y=2. 2.2. y=-5. 2.3. y=x. 2.4. y=2x+2. 2.5. y=  2.6. y=
2.6. y= 
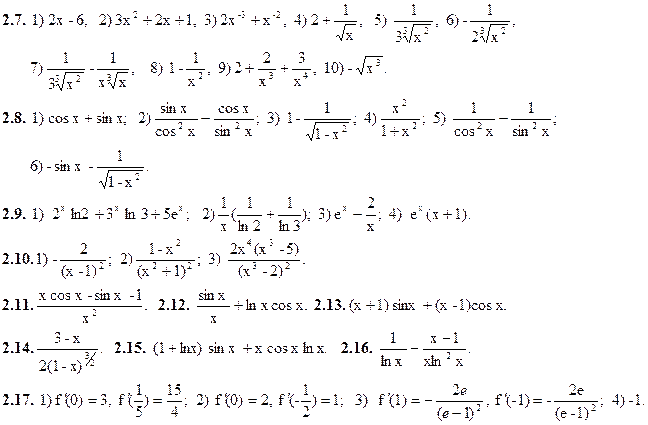


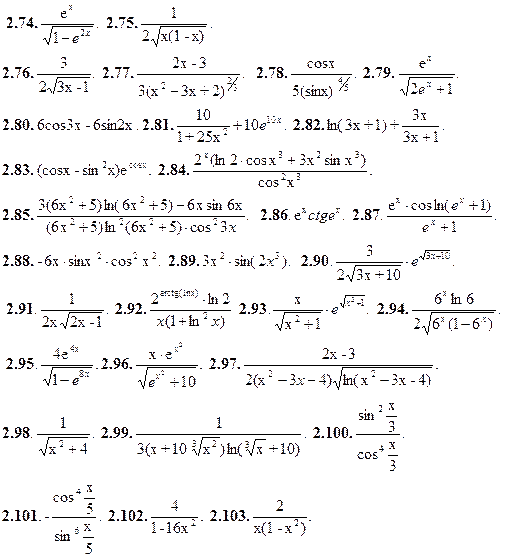


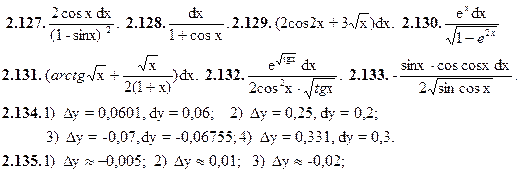

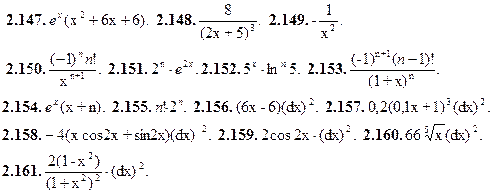
2.162. 1) Нет; 2) нет; 3) нет. 2.163. Нет.
2.164.  5) условия теоремы Ролля не выполнены; 6) условия теоремы Ролля не выполнены.
5) условия теоремы Ролля не выполнены; 6) условия теоремы Ролля не выполнены.
2.166. 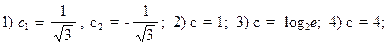 5) теорема Лагранжа неприменима. 2.167.
5) теорема Лагранжа неприменима. 2.167.  2.168. M(1; 1).
2.168. M(1; 1).
 2.172. Нет. Не выполнено условие
2.172. Нет. Не выполнено условие 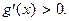 2.173. 1. 2.174. 2, 5. 2.175. 2. 2.176. 1. 2.177. 0. 2.178. 0. 2.179. 1. 2.180. 1. 2.181. 0. 2.182.
2.173. 1. 2.174. 2, 5. 2.175. 2. 2.176. 1. 2.177. 0. 2.178. 0. 2.179. 1. 2.180. 1. 2.181. 0. 2.182.  . 2.183. 0. 2.184.
. 2.183. 0. 2.184.  2.185. 3.
2.185. 3.

2.203. 1) При х=-1 - максимум, f(-1)=10; при х=3 - минимум, f(3)=-22; на (-  ; -1) и на (3; +
; -1) и на (3; +  ) функция возрастает, на (-1; 3) функция убывает; 2) при х=1 - максимум, f(1)=-4; при х=5 - минимум, f(5)=4; на
) функция возрастает, на (-1; 3) функция убывает; 2) при х=1 - максимум, f(1)=-4; при х=5 - минимум, f(5)=4; на  и на
и на  функция возрастает; на (1; 3) и на (3; 5) функция убывает; 3) при х=
функция возрастает; на (1; 3) и на (3; 5) функция убывает; 3) при х=  - минимум, f(
- минимум, f(  )=-
)=-  ; на (0;
; на (0;  ) функция убывает, на(
) функция убывает, на(  ; +
; +  ) функция возрастает; 4) при х=-
) функция возрастает; 4) при х=-  - максимум,
- максимум,
f(-  )=
)=  при х=
при х=  - минимум, f(
- минимум, f(  )=
)= 
 на
на  и на
и на  функция возрастает, на (-
функция возрастает, на (-  ;
;  ) функция убывает; 5) при х=0 - минимум,
) функция убывает; 5) при х=0 - минимум,
f(0)=0; при х=2 - максимум, f(2)=4e-2; на (-  ; 0) и на (2; +
; 0) и на (2; +  ) функция убывает; на (0; 2) функция возрастает. 2.204. 1) при х=4 - точка перегиба; на (-
) функция убывает; на (0; 2) функция возрастает. 2.204. 1) при х=4 - точка перегиба; на (-  ; 4) - выпуклость вверх, на (4; +
; 4) - выпуклость вверх, на (4; +  ) - вниз; 2) при
) - вниз; 2) при 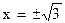 и при х=0 - точки перегиба; на (-
и при х=0 - точки перегиба; на (-  , -
, -  ) и на (0,
) и на (0,  ) - выпуклость вверх, на (-
) - выпуклость вверх, на (-  , 0) и на (
, 0) и на (  , +
, +  ) - выпуклость вниз; 3) при
) - выпуклость вниз; 3) при  - точка перегиба; на (0,
- точка перегиба; на (0,  ) - выпуклость вверх, на (
) - выпуклость вверх, на (  , +
, +  ) - вниз; 4) точек перегиба нет; на (-
) - вниз; 4) точек перегиба нет; на (-  , +
, +  ) выпуклость вниз.
) выпуклость вниз.
2.205.При х=0 - максимум, у(0)=1; при х=  - точки перегиба; у=0 - горизонтальная асимптота; функция положительна.2.206. При х=2 - максимум, у(2)=16; при х=-2 - минимум, у=-16; при х=0 - точка перегиба. 2.207. При х=-1 - максимум, у(-1)=0; х=0, х=-2 - вертикальные асимптоты, у=1 - горизонтальная асимптота. 2.208. Экстремальных точек нет. х=
- точки перегиба; у=0 - горизонтальная асимптота; функция положительна.2.206. При х=2 - максимум, у(2)=16; при х=-2 - минимум, у=-16; при х=0 - точка перегиба. 2.207. При х=-1 - максимум, у(-1)=0; х=0, х=-2 - вертикальные асимптоты, у=1 - горизонтальная асимптота. 2.208. Экстремальных точек нет. х=  - вертикальные асимптоты, у=0 - горизонтальная асимптота. 2.209. При х=2 - максимум, у(2)=
- вертикальные асимптоты, у=0 - горизонтальная асимптота. 2.209. При х=2 - максимум, у(2)=  при х = 2+
при х = 2+  - точка перегиба; у=0 - горизонтальная асимптота при х
- точка перегиба; у=0 - горизонтальная асимптота при х  . 2.210. При х=1 - минимум, у(1)=е; точек перегиба нет; х=0 - вертикальная асимптота; у=0 - горизонтальная асимптота при х
. 2.210. При х=1 - минимум, у(1)=е; точек перегиба нет; х=0 - вертикальная асимптота; у=0 - горизонтальная асимптота при х  . 2.211. При х=1 - минимум, у(1)=0; при х=
. 2.211. При х=1 - минимум, у(1)=0; при х=  - максимум, у(е-2)=4е-2;
- максимум, у(е-2)=4е-2; 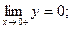 функция неотрицательна. 2.212. При х=1 - минимум, у(1)=1; точек перегиба нет; х=0 - вертикальная асимптота; функция неотрицательна. 2.213. При х=2 - минимум, у(2)=2; при х=-2 - максимум, у(-2)=-2; х=0 - вертикальная асимптота, у=
функция неотрицательна. 2.212. При х=1 - минимум, у(1)=1; точек перегиба нет; х=0 - вертикальная асимптота; функция неотрицательна. 2.213. При х=2 - минимум, у(2)=2; при х=-2 - максимум, у(-2)=-2; х=0 - вертикальная асимптота, у=  - наклонная асимптота.2.214. При х=0 - максимум, у(0)=0; при х=2 - минимум, у(2)=4; х=1 - вертикальная асимптота, у=х+1 - наклонная асимптота. 2.215. Экстремальных точек нет. При х=0 - точка перегиба; у=х+
- наклонная асимптота.2.214. При х=0 - максимум, у(0)=0; при х=2 - минимум, у(2)=4; х=1 - вертикальная асимптота, у=х+1 - наклонная асимптота. 2.215. Экстремальных точек нет. При х=0 - точка перегиба; у=х+  - наклонная асимптота при х
- наклонная асимптота при х  , у=х-
, у=х-  - наклонная асимптота при х
- наклонная асимптота при х  . 2.216. При х=-
. 2.216. При х=-  -максимум,
-максимум,
у(-  )=
)=  ; при х=
; при х=  - минимум, у(
- минимум, у(  )=
)= 
 ; у=х
; у=х  - наклонная асимптота при х
- наклонная асимптота при х  ; у=х
; у=х  - наклонная асимптота при х
- наклонная асимптота при х  . 2.217. При х=1 - максимум, у(1)=1; при х=
. 2.217. При х=1 - максимум, у(1)=1; при х=  - точка перегиба; х=0 - вертикальная асимптота при х
- точка перегиба; х=0 - вертикальная асимптота при х 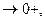 у=0 - горизонтальная асимптота при х
у=0 - горизонтальная асимптота при х  . 2.218. При х=
. 2.218. При х=  - минимум, у(
- минимум, у( 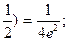 точек перегиба нет; х=0 - вертикальная асимптота при х
точек перегиба нет; х=0 - вертикальная асимптота при х 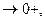
 2.219.
2.219. 
 причем
причем  . 2.222. 50 м и 100м. 2.223. 2. 2.224. 50
. 2.222. 50 м и 100м. 2.223. 2. 2.224. 50  км/час
км/час  км/час. 2.225. 20 строк; 5200 у.е. 2.226. 1475 кг. 2.227. При х
км/час. 2.225. 20 строк; 5200 у.е. 2.226. 1475 кг. 2.227. При х  (0; 100) финансовые накопления возрастают, при х
(0; 100) финансовые накопления возрастают, при х  (100, +
(100, +  ) - убывают. 2.228. С увеличением объема выпуска продукции издержки увеличиваются. 2.229. В точке (1, 5; 3, 375); у=6, 75х - 6, 75. 2.230. а=
) - убывают. 2.228. С увеличением объема выпуска продукции издержки увеличиваются. 2.229. В точке (1, 5; 3, 375); у=6, 75х - 6, 75. 2.230. а=  2.231. При р> 2
2.231. При р> 2  спрос эластичен, при 0 < p < 2
спрос эластичен, при 0 < p < 2  - неэластичен, при р=2
- неэластичен, при р=2  - нейтрален. 2.232. Если
- нейтрален. 2.232. Если  то спрос при любых р
то спрос при любых р  эластичен; если 0 <
эластичен; если 0 <  < 1, то спрос неэластичен; если
< 1, то спрос неэластичен; если  , то спрос нейтрален. 2.233. 1) При х
, то спрос нейтрален. 2.233. 1) При х  торговля прибыльная, при х
торговля прибыльная, при х  и при х
и при х  - торговля убыточная; х*=10, р*=125, Vmax=75; 2)При х
- торговля убыточная; х*=10, р*=125, Vmax=75; 2)При х  торговля прибыльная, при х
торговля прибыльная, при х  и при х
и при х  - торговля убыточная; х*=10, р*=80, Vmax=125; 3) При х
- торговля убыточная; х*=10, р*=80, Vmax=125; 3) При х  торговля прибыльная, при х
торговля прибыльная, при х  и при х
и при х  - торговля убыточная; х*=25, р*=2, Vmax=4; 4) При х
- торговля убыточная; х*=25, р*=2, Vmax=4; 4) При х  - торговля прибыльная, при х
- торговля прибыльная, при х  и при х
и при х  - торговля убыточная; х*=2, 5(
- торговля убыточная; х*=2, 5(  , р*
, р*  Vmax
Vmax  2.234. 1)При х
2.234. 1)При х 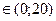 торговля убыточная, при х
торговля убыточная, при х  - торговля прибыльная; так как V(х) - возрастающая функция при всех х, то точек максимума у нее нет; 2) при х
- торговля прибыльная; так как V(х) - возрастающая функция при всех х, то точек максимума у нее нет; 2) при х  торговля прибыльная, при х
торговля прибыльная, при х 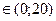 и при х
и при х  торговля убыточная; х*=32, 5, Vmax=1562, 5; 3) при х
торговля убыточная; х*=32, 5, Vmax=1562, 5; 3) при х  (30; 40) торговля прибыльная, при х
(30; 40) торговля прибыльная, при х  (0; 30) и при х
(0; 30) и при х  (40; +
(40; +  ) торговля убыточная; х*=35, Vmax=200. 2.235. 1) При р0
) торговля убыточная; х*=35, Vmax=200. 2.235. 1) При р0  ; 2) при р0
; 2) при р0  ; 3) при р0
; 3) при р0  ; 4) при р0
; 4) при р0  2.236.1)При р0
2.236.1)При р0  5; 2)при р0
5; 2)при р0  2.237. 1) При любых b0
2.237. 1) При любых b0  2) при b0
2) при b0  3) при b0
3) при b0  2.238. 1) При b1
2.238. 1) При b1  ; 2) при b1
; 2) при b1  3) при b1
3) при b1  4) при b1
4) при b1 
Тема 3.
3.1. 1) если а 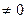 , то F(a, 0)=
, то F(a, 0)= 
3.2. 1) Вся плоскость, кроме точки (0, 0); 2) вся плоскость, кроме точек прямой у=-х; 3) круг х2+у2  радиуса 1 с центром в начале координат; 4) I и III квадранты, исключая точки, лежащие на осях координат; 5) вся плоскость, кроме точек прямых у=х и у=-х; 6) полуплоскость, лежащая ниже прямой у=х, включая эту прямую; 7) круг х2+у2
радиуса 1 с центром в начале координат; 4) I и III квадранты, исключая точки, лежащие на осях координат; 5) вся плоскость, кроме точек прямых у=х и у=-х; 6) полуплоскость, лежащая ниже прямой у=х, включая эту прямую; 7) круг х2+у2  радиуса 1 с центром в начале координат.
радиуса 1 с центром в начале координат.
3.6. 2х 
3.7. 



3.36. Координаты вектора  таковы: 1) (-2, -4); 2) (2, -1); 3) (2, 1);
таковы: 1) (-2, -4); 2) (2, -1); 3) (2, 1);
4) (-2, 1).
 3.40.zmin=6 при х=-1, у=2. 3.41. zmax=22 при х=2, у=1. 3.42. Экстремума нет.
3.40.zmin=6 при х=-1, у=2. 3.41. zmax=22 при х=2, у=1. 3.42. Экстремума нет.
3.43. zmin=0 при х=1, у=  3.44. zmin=0 при х=у=0. 3.45. zmax=12 при х=у=4.
3.44. zmin=0 при х=у=0. 3.45. zmax=12 при х=у=4.
3.46.zmin=  при х=0, у=-1. 3.47. zнаим. =-16 при х=3, у=2; zнаиб.=-4 при х=2, у=0. 3.48. zнаим. =5 при х=у=0 и при х=1, у=2; zнаиб.=7 при х=0, у=2 и при х=1, у=0. 3.49. zнаим. =1 при х=у=1; zнаиб.=13 при х=3, у=-1. 3.50. zнаим. =0 при х=у=0; zнаиб.=1, 5
при х=0, у=-1. 3.47. zнаим. =-16 при х=3, у=2; zнаиб.=-4 при х=2, у=0. 3.48. zнаим. =5 при х=у=0 и при х=1, у=2; zнаиб.=7 при х=0, у=2 и при х=1, у=0. 3.49. zнаим. =1 при х=у=1; zнаиб.=13 при х=3, у=-1. 3.50. zнаим. =0 при х=у=0; zнаиб.=1, 5  при х=у=
при х=у=  . 3.51. zmin=2 при х=у=1. 3.52. zmin=-4 при х=у=-2; zmax=4 при х=у=2. 3.53.zmax=1 при х=у=
. 3.51. zmin=2 при х=у=1. 3.52. zmin=-4 при х=у=-2; zmax=4 при х=у=2. 3.53.zmax=1 при х=у=  1; zmin=-1 при х=-у=
1; zmin=-1 при х=-у=  .
.
Тема 4.








4.171. 1) интеграл расходится; 2) интеграл расходится; 3)1; 4) при 0< а 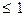 интеграл расходится, при а> 1 интеграл равен
интеграл расходится, при а> 1 интеграл равен  . 4.172. 1) расходится; 2) 1.
. 4.172. 1) расходится; 2) 1.
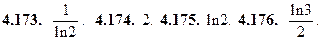 4.177. Расходится.
4.177. Расходится.
 Расходится. 4.182. Расходится.
Расходится. 4.182. Расходится.
4.183. -1. 4.184. 1. 4.185. 1) 2; 2) расходится; 3) расходится;
4) при 0< a< 1 интеграл равен 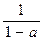 , при а
, при а  интеграл расходится.
интеграл расходится.
4.186. Расходится. 4.187.  4.189. Расходится.
4.189. Расходится.
 4.192. Расходится. 4.193.
4.192. Расходится. 4.193. 
Тема 5.
5.1.Да. 5.2.Да. 5.3.Нет. 5.4.При С=0 - является, при С  0 - нет.
0 - нет.
5.5.  5.6.
5.6.  5.7.
5.7. 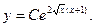
5.8.  5.9.
5.9.  5.10.
5.10. 

Тема 6.

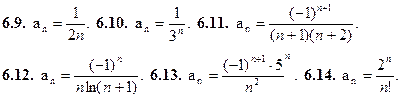
6.15.Нет. 6.16.Нет. 6.17.Да. 6.18.Да. 6.19.Да. 6.20.Да.
6.21.Нет. 6.22.Да. 6.23.Да. 6.24.Да. 6.25.Расходится. 6.26.Расходится.
6.27.Сходится. 6.28.Сходится. 6.29.Расходится, так как 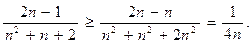 6.30.Сходится. 6.31.Сходится.
6.30.Сходится. 6.31.Сходится.
6.32.Сходится.
6.33.Сходится. 6.34.Сходится. 6.35.Сходится. 6.36.Расходится.
6.37.Сходится.
6.38.Сходится. 6.39.Сходится. 6.40.Сходится. 6.41.Сходится.
6.42.Расходится.
6.43.Расходится. 6.44.Сходится. 6.45. Сходится. 6.46. Сходится.
6.47. Сходится. 6.48.Расходится. 6.49.При 0< a 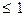 ряд расходится, при а> 1 ряд сходится. 6.50. Сходится. 6.51.Сходится. 6.52.Расходится. 6.53.Расходится. 6.54.Сходится.
ряд расходится, при а> 1 ряд сходится. 6.50. Сходится. 6.51.Сходится. 6.52.Расходится. 6.53.Расходится. 6.54.Сходится.
6.55.Условно сходится. 6.56.Условно сходится. 6.57.Абсолютно сходится.
6.58.Абсолютно сходится. 6.59.Абсолютно сходится. 6.60.Абсолютно сходится.
6.61.Абсолютно сходится. 6.62.Абсолютно сходится. 6.63.Расходится.
6.64.Расходится. 6.65.Условно сходится. 6.66.Условно сходится.
6.67.Абсолютно сходится. 6.68.Абсолютно сходится. 6.69.Условно сходится.
6.70.Условно сходится. 6.71.Расходится. 6.72.Расходится. 6.73.Абсолютно сходится.
6.74.Абсолютно сходится. 6.75.Условно сходится. 6.76.Условно сходится.
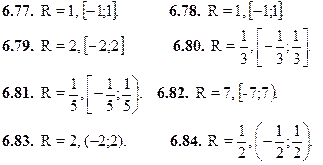
6.85. R=  . Ряд сходится абсолютно на всей числовой прямой.
. Ряд сходится абсолютно на всей числовой прямой.
6.86. R=  . Ряд сходится абсолютно на всей числовой прямой.
. Ряд сходится абсолютно на всей числовой прямой.
6.87. R=0. Ряд расходится на всей числовой прямой, кроме точки х=0.
6.88. R=0. Ряд расходится на всей числовой прямой, кроме точки х=0.
6.89.R=3, (-3; 3).6.90.R=1, (-1; 1).6.91.R=1, (-1; 1).6.92. R=1, [-1; 1].
6.93. R=6, (-6; 6]. 6.94. R=1, [-1; 1]. 6.95. R=  . 6.96.
. 6.96. 


Указание: разложите квадратный трехчлен на множители.


