Численное решение нелинейного уравнения. Этапы решения.
f(x)=0, где f(x) – произвольная функция, наиболее распространенная в инж. Практике задача по отысканию корней.
Выбор метода решения зависит от вида f(x). Для численного решения нелинейных уравнений применяются только итерационные методы.
Задача нахождения корней состоит из 2 этапов:
1. Отделение корней – определение числа корней и их примерного расположения на числовой оси.
Наиболее применим графический способ отделения корней, т. е. отыскание точек пересечения ф. f(x) с осью абсцисс:
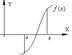 [a; b] – интервал изоляции корня. Для каждого корня уравнения определяется интервал его изоляции [a; b]. На отрезке [a; b] должен находиться 1 корень.
[a; b] – интервал изоляции корня. Для каждого корня уравнения определяется интервал его изоляции [a; b]. На отрезке [a; b] должен находиться 1 корень.
2. Уточнение корней – вычисление каждого корня с заданной степенью точности.
Классификация методов уточнения корней:
1) Метод половинного деления отрезка(дихотомии).
 Отрезок [a; b], содержащий единственный корень, делят пополам, отбрасывают ту половину, где нет корня. Процесс повторяется до тех пор, пока длина отрезка не станет меньше заданной погр. E.
Отрезок [a; b], содержащий единственный корень, делят пополам, отбрасывают ту половину, где нет корня. Процесс повторяется до тех пор, пока длина отрезка не станет меньше заданной погр. E.
Достоинства: прост и надежен, всегда сводится к решению независимо от вида ф. f(x). Недостаток: самый медленный из всех известных методов уточн. Корня.
2) Метод хорд.
 Построение последовательных хорд, в качестве приближений к корню принимаются значения их пересечения с осью абсцисс.
Построение последовательных хорд, в качестве приближений к корню принимаются значения их пересечения с осью абсцисс.
Достоинство: простота. Недостаток: быстрота сходимости к решению сильно зависит от вида ф. f(x).
 3) Метод касательных( метод Ньютона)
3) Метод касательных( метод Ньютона)
В качестве приближения к корню ищется точка пересечения касательной с осью абсцисс.
Достоинство: высокая скорость. Недостатки: ограничения на вид ф. (должна быть дифференцируема, f’(x) и f’’(x) не должны менять знак на интервале уточнения корня).
4) Комбинированный метод – объединение методов хорд и касательных.
 Приближение к корню на каждой итерации происходит одновременно с 2 сторон интервала [a; b]. Одной стороны строится хорда, а с другой касательная.
Приближение к корню на каждой итерации происходит одновременно с 2 сторон интервала [a; b]. Одной стороны строится хорда, а с другой касательная.
Достоинство: работает быстрее, чем методы хорд и касательных. Недостатки: f(x) должна быть дифференцируема; f’(x) иf’’(x) не должны менять знак на интервале уточнения корня; трудности с дифф-ем f(x).
5) Метод простой итерации.
Исходное нелинейное уравнения заменяется равносильным уравнением x=g(x)и с помощью сходящегося итерационного процесса происходит приближение к корню, пока не достигнет предела заданной погрешности Е.
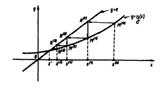
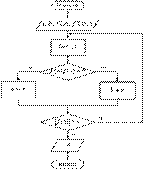
45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм.
Требуется вычислить корень уравнения f(x)=0 на [a; b] с заданной погрешностью Е.
Отрезок [a; b], содержащий единственный корень, делят на 2 половины, отбрасывают ту из них, где нет корня. Процесс продолжается до тех пор, пока длина отрезка не станет меньше заданной погрешности Е.
 Алгоритм метода:
Алгоритм метода:
|
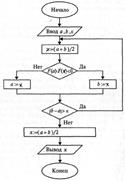
 46)Уточнение корня нелинейного уравнения методом хорд. Схема алгоритма. Требуется вычислить корень уравнения f(x)=0 на [a, b] с заданной погрешностью е. Геометр-ки метод основан на построении последовательности хорд. Ур-е хорды
46)Уточнение корня нелинейного уравнения методом хорд. Схема алгоритма. Требуется вычислить корень уравнения f(x)=0 на [a, b] с заданной погрешностью е. Геометр-ки метод основан на построении последовательности хорд. Ур-е хорды  . В данном методе процесс итерации состоит в том, что в качестве приближений к корню уравнение f(x)=0 принимаются значения х1, х2… хi точек пересечения хорды АВ с осью абсцисс. Если f(a)> 0, то левая граница a неподвижна, х0=b и из урав. хорды получим:
. В данном методе процесс итерации состоит в том, что в качестве приближений к корню уравнение f(x)=0 принимаются значения х1, х2… хi точек пересечения хорды АВ с осью абсцисс. Если f(a)> 0, то левая граница a неподвижна, х0=b и из урав. хорды получим:  Если f(a)< 0, то правая граница b неподвижна, x0=a.
Если f(a)< 0, то правая граница b неподвижна, x0=a. 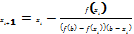 .
.
Алгоритм:
 где Det_x
где Det_x 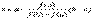
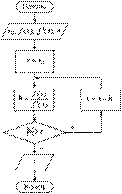
47) Уточнение корня нелинейного уравнения методом касательных. Схема алгоритма.
 Отличие от м.хорд – вместо хорды на каждом шаге проводится касательная к кривой y=f(x) и в качестве приближения к корню ищется точка пересечения касательной с осью абсцисс. Уравн-е касательной проведенной в т. х0:
Отличие от м.хорд – вместо хорды на каждом шаге проводится касательная к кривой y=f(x) и в качестве приближения к корню ищется точка пересечения касательной с осью абсцисс. Уравн-е касательной проведенной в т. х0: 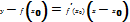 . Правило: В качестве исходной точки х0 выбирается тот конец интервала [a, b], где знак ф-и совпадает со знаком 2й производной f’’(x). Из уравнения касательной найдем след.приближение корня х1, как абсциссу точки пересечения касательной с осью ох:
. Правило: В качестве исходной точки х0 выбирается тот конец интервала [a, b], где знак ф-и совпадает со знаком 2й производной f’’(x). Из уравнения касательной найдем след.приближение корня х1, как абсциссу точки пересечения касательной с осью ох: 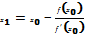 . Аналогично м. б. найдены и последующие приближенно. Ф-ла для i+1 приближения имеет вид:
. Аналогично м. б. найдены и последующие приближенно. Ф-ла для i+1 приближения имеет вид: 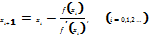 Для окончания можно использовать условия |f(xi)|< e или |xi+1-xi|< e.
Для окончания можно использовать условия |f(xi)|< e или |xi+1-xi|< e.
Алгоритм:
 48) Уточнение корня нелинейного уравнения комбинированным методом. Схема алгоритма. Геометрически такое объединение сводится к тому, что приближение к истинному значению корня уравнения f(x)=0 на каждой итерации происходит одновременно с 2х сторон интервала [a, b]. При это, для приближения к корню с одной стороны строится хорда, а с др.- касательная. Пусть для определенности f’(x)> 0 и f’’(x)> 0 при a≤ x≤ b. Тогда для приближения к корню со стороны границы а используем построение хорды, а со стороны границы b – касательная. На 1й итерации строим хорду А0В0 и проводим касательную в точку В0. Левую границу а переносим в а1, правую – b1. На каждой итерации для вычисления новых границ интервала используют ф-лы хорд и касательных:
48) Уточнение корня нелинейного уравнения комбинированным методом. Схема алгоритма. Геометрически такое объединение сводится к тому, что приближение к истинному значению корня уравнения f(x)=0 на каждой итерации происходит одновременно с 2х сторон интервала [a, b]. При это, для приближения к корню с одной стороны строится хорда, а с др.- касательная. Пусть для определенности f’(x)> 0 и f’’(x)> 0 при a≤ x≤ b. Тогда для приближения к корню со стороны границы а используем построение хорды, а со стороны границы b – касательная. На 1й итерации строим хорду А0В0 и проводим касательную в точку В0. Левую границу а переносим в а1, правую – b1. На каждой итерации для вычисления новых границ интервала используют ф-лы хорд и касательных:  ,
, 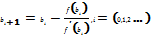 . Сужение интервала проводим до тех пор пока он не станет < зад.погрешности |bi+1-ai+1|< e. За значение корня можно взять среднее арифметическое полученных границ интервала.
. Сужение интервала проводим до тех пор пока он не станет < зад.погрешности |bi+1-ai+1|< e. За значение корня можно взять среднее арифметическое полученных границ интервала.
Алгоритм:


