| Вопрос
| Ответы
|
| 1. Указать соответствие, заданное уравнением, которое не является функцией
| 1)  ; 2) ; 2)  ; 3)* ; 3)*  ;
4) ;
4)  ; 5) ; 5) 
|
2. Областью определения функции 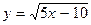 является промежуток: является промежуток:
| 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  ; 5)* ; 5)* 
|
3. Областью определения функции 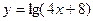 является промежуток: является промежуток:
| 1) 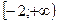 ; 2)* ; 2)*  ; 3) ; 3)  ; 4) ; 4)  ; 5) ; 5) 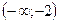
|
4. Областью определения функции 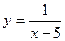 является промежуток: является промежуток:
| 1) 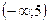 ; 2) ; 2) 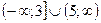 ; 3)* ; 3)*  ;
4) ;
4)  ; 5) ; 5) 
|
5. Областью значений функции  является промежуток: является промежуток:
| 1) 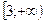 ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 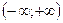 ; 5)* ; 5)* 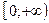
|
6. Областью значений функции 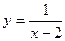 является промежуток: является промежуток:
| 1)  ; 2)* ; 2)*  ; 3) ; 3) 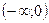 ; 4) ; 4) 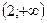 ;
5) ;
5) 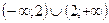
|
7. Областью значений функции  является промежуток: является промежуток:
| 1) 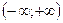 ; 2) ; 2) 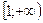 ; 3) ; 3) 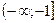 ; 4)* ; 4)*  ; 5) ; 5) 
|
| 8. Указать функцию, которая не является сложной:
| 1)  ; 2) ; 2) 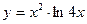 ; 3) ; 3)  ;
4)* ;
4)* 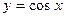 ; 5) ; 5) 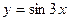
|
| 9. Указать функцию, которая является сложной:
| 1) 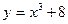 ; 2) ; 2) 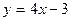 ; 3) ; 3)  ;
4) ;
4)  ; 5)* ; 5)* 
|
10. Предел  равен: равен:
| 1) 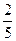 ; 2) 0; 3) 1; 4) ; 2) 0; 3) 1; 4)  ; 5)* ; 5)* 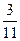
|
11. Предел  равен: равен:
| 1)*  ; 2) ; 2)  ; 3) 1; 4) – 2; 5) ; 3) 1; 4) – 2; 5) 
|
12. Предел 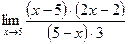 равен: равен:
| 1) 1; 2)  ; 3) ; 3)  ; 4)* ; 4)*  ; 5) ; 5) 
|
13. Используя свойства пределов функций, найти предел 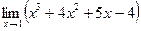 . .
| 1) 2; 2) 3; 3) 21; 4)*6; 5) 5
|
14. Используя свойства пределов функций, найти предел 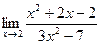 . .
| 1)  ; 2)* ; 2)*  ; 3) ; 3) 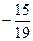 ; 4) ; 4)  ; 5) ; 5) 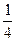
|
| 15. Указать первый замечательный предел.
| 1)  ; 2) ; 2)  ; 3) ; 3) 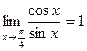 ;
4) ;
4)  ; 5)* ; 5)* 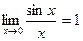
|
16. Предел 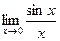 равен: равен:
| 1) 0; 2) 2; 3) 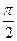 ; 4)* 1; 5) ; 4)* 1; 5) 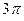
|
| 17. Указать второй замечательный предел.
| 1) 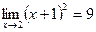 ; 2) ; 2)  ; 3)* ; 3)*  ;
4) ;
4)  ; 5) ; 5) 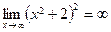
|
18. Предел 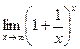 равен: равен:
| 1)  ; 2) 0; 3)* ; 2) 0; 3)* 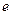 ; 4) 2; 5) 3 ; 4) 2; 5) 3
|
19. Указать множество точек плоскости  , которое не является графиком функции , которое не является графиком функции 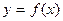 . .
| 1)*

| 2)
|
3)

| 4)

|
5)

|
|
20. Предел  равен: равен:
| 1) – 2; 2) – 4; 3) 1; 4)* 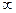 ; 5) 0 ; 5) 0
|
21. Предел 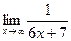 равен: равен:
| 1) 3; 2) 2; 3)*0; 4) 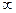 ; 5) – 1 ; 5) – 1
|
22. Предел 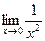 равен: равен:
| 1) 3; 2)* 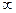 ; 3) 2; 4) 0; 5) – 1 ; 3) 2; 4) 0; 5) – 1
|
23. Функция 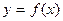 , определенная на интервале , определенная на интервале 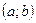 , называется непрерывной в точке , называется непрерывной в точке 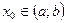 , если: , если:
| 1)*  ; 2) ; 2)  ; 3) ; 3)  ;
4) ;
4)  ; 5) ; 5) 
|
24. Графиком функции 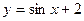 является кривая: является кривая:
| 1)

| 2)
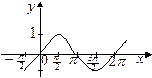
|
3)*

| 4)

|
5)
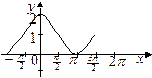
|
|
25. Предел функции 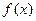 в точке в точке 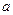 существует и равен существует и равен 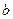  , если: , если:
| 1) существует предел справа 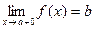 ;
2) существует предел слева ;
2) существует предел слева  ;
3) существуют левосторонний и правосторонний пределы
4)* существуют односторонние пределы, равные между собой, т.е. ;
3) существуют левосторонний и правосторонний пределы
4)* существуют односторонние пределы, равные между собой, т.е. 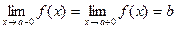 ;
5) функция ;
5) функция 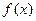 — постоянная — постоянная
|
26. Точкой разрыва функции 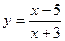 является точка: является точка:
| 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4)* ; 4)*  ; 5) ; 5) 
|
27. Если функция 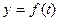 — функция, непрерывная на отрезке — функция, непрерывная на отрезке  , причем ее значения принадлежат отрезку , причем ее значения принадлежат отрезку  ; ;  — функция, непрерывная на отрезке — функция, непрерывная на отрезке  , то сложная функция , то сложная функция 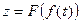 непрерывна в промежутке: непрерывна в промежутке:
| 1)*  ;
2) ;
2)  ;
3) ;
3)  ;
4) ;
4)  ;
5) ;
5) 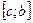
|
28. Графиком функции 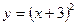 является кривая: является кривая:
| 1)

| 2)*
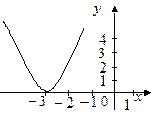
|
3)

| 4)

|
5)

|
|
29. Областью непрерывности функции 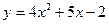 является множество: является множество:
| 1)  ; 2) ; 2) 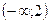 ; 3) ; 3)  ; 4) ; 4)  ; 5)* ; 5)* 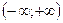
|
30. Непрерывной на множестве 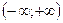 является функция: является функция:
| 1)*  ; 2) ; 2) 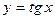 ; 3) ; 3)  ; 4) ; 4) 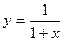 ; 5) ; 5) 
|
31. Графиком функции 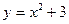 является кривая: является кривая:
| 1)
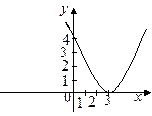
| 2)*
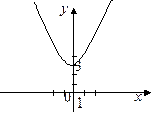
|
3)

| 4)

|
5)

|
|
| | | | |
| Вопрос
| Ответы
|
1. Предел отношения (если он существует) приращения 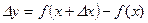 функции функции 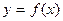 в точке в точке 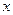 к приращению к приращению 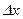 аргумента, при условии, что приращение аргумента аргумента, при условии, что приращение аргумента 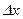 стремится к нулю, т.е. стремится к нулю, т.е.  , называется: , называется:
| 1) непрерывностью 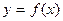 в точке в точке 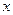 ;
2) приращением аргумента ;
2) приращением аргумента 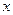 ;
3) приращением функции ;
3) приращением функции 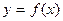 в точке в точке 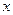 ;
4) *производной функции ;
4) *производной функции 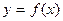 в точке в точке 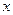 ;
5) пределом функции ;
5) пределом функции 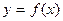 в точке в точке 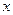
|
2. Если в некоторой точке 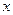 функции функции 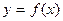 и и 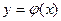 имеют производные, то производная от суммы этих функций имеют производные, то производная от суммы этих функций 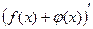 равна: равна:
| 1) 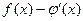 ; 2) ; 2) 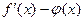 ; 3) ; 3)  ;
4) ;
4) 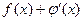 ; 5)* ; 5)* 
|
3. Если в точке 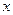 функции функции 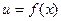 и и 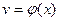 имеют производные, то в точке имеют производные, то в точке 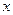 произведение этих функций имеет производную, которая равна: произведение этих функций имеет производную, которая равна:
| 1) 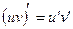 ; 2) ; 2) 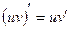 ; 3)* ; 3)* 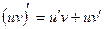 ;
4) ;
4) 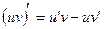 ; 5) ; 5) 
|
4. Производная функции  равна: равна:
| 1) 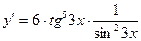 ; 2) ; 2)  ;
3) ;
3) 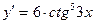 ; 4) ; 4)  ; 5)* ; 5)* 
|
5. Угловой коэффициент касательной к графику функции  в точке в точке  равен: равен:
| 1) 4; 2)* 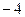 ; 3) ; 3)  ; 4) –2; 5) 5 ; 4) –2; 5) 5
|
6. Если в точке 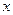 функции функции 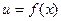 и и 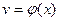 имеют производные, причем в этой точке функция имеют производные, причем в этой точке функция  отлична от нуля, то частное этих функций имеет в точке отлична от нуля, то частное этих функций имеет в точке 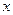 производную, которая вычисляется по формуле: производную, которая вычисляется по формуле:
| 1) 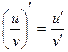 ; 2)* ; 2)* 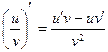 ; 3) ; 3)  ;
4) ;
4) 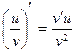 ; 5) ; 5) 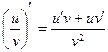
|
7. Для нахождения производной функции 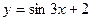 в точке в точке  необходимо найти значение выражения: необходимо найти значение выражения:
| 1)  ; 2) ; 2)  ;
3) ;
3) 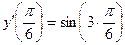 ; 4) ; 4) 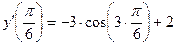 ;
5)* ;
5)* 
|
8. Производная функции  равна: равна:
| 1)  ; 2)* ; 2)* 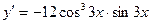 ; 3) ; 3) 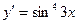 ;
4) ;
4) 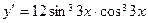 ; 5) ; 5) 
|
9. Производная функции  равна: равна:
| 1) 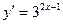 ; 2) ; 2) 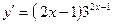 ; 3)* ; 3)* 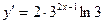 ;
4) ;
4) 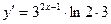 ; 5) ; 5) 
|
10. Производная функции 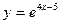 равна: равна:
| 1)* 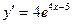 ; 2) ; 2)  ; 3) ; 3)  ;
4) ;
4) 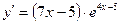 ; 5) ; 5) 
|
11. Найти дифференциал функции 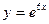 . .
| 1)  ; 2) ; 2)  ; 3) ; 3) 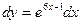 ;
4)* ;
4)* 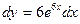 ; 5) ; 5) 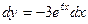
|
12. Эластичность функции 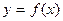 определяется формулой: определяется формулой:
| 1)  ; 2) ; 2) 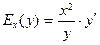 ; 3) ; 3)  ;
4) ;
4) 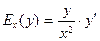 ; 5)* ; 5)* 
|
| Вопрос
| Ответы
|
1. Пусть функция 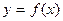 определена на определена на  и во внутренней точке и во внутренней точке 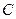 промежутка принимает наибольшее или наименьшее значение. Если существует конечная производная промежутка принимает наибольшее или наименьшее значение. Если существует конечная производная  , то необходимо, чтобы: , то необходимо, чтобы:
| 1)  ; 2) ; 2) 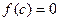 ; 3) ; 3)  ; 4) ; 4) 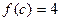 ; 5)* ; 5)* 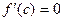
|
2. Если 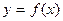 и и 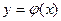 — дифференцируемые бесконечно малые или бесконечно большие функции при — дифференцируемые бесконечно малые или бесконечно большие функции при  , то имеет место равенство (правило Лопиталя): , то имеет место равенство (правило Лопиталя):
| 1)  ; 2) ; 2)  ;
3)* ;
3)*  ; 4) ; 4) 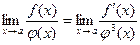 ;
5) ;
5) 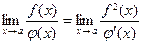
|
3. Пусть функция 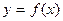 определена на множестве определена на множестве  и внутри его имеет конечную производную и внутри его имеет конечную производную 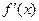 . Для того, чтобы . Для того, чтобы 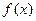 была постоянной на была постоянной на  , необходимо и достаточно, чтобы внутри , необходимо и достаточно, чтобы внутри  выполнялось равенство: выполнялось равенство:
| 1)  ;
2)* ;
2)*  ;
3) ;
3) 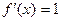 ;
4) ;
4)  ;
5) ;
5) 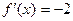
|
4. Точкой экстремума функции  является точка: является точка:
| 1) 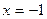 ; 2) ; 2) 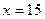 ; 3) ; 3)  ; 4) ; 4)  ; 5)* ; 5)* 
|
5. Если в некотором промежутке производная данной функции 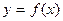 положительна, т.е. положительна, т.е.  , то функция в этом промежутке: , то функция в этом промежутке:
| 1 )* возрастает; 2) имеет максимум; 3) убывает;
4) постоянна; 5) имеет минимум
|
6. Кривая 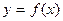 выпукла вверх на интервале выпукла вверх на интервале 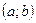 , если во всех точках этого интервала выполняется соотношение: , если во всех точках этого интервала выполняется соотношение:
| 1)  ; 2) ; 2)  ; 3) ; 3) 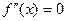 ; 4) ; 4)  ; 5)* ; 5)* 
|
7. Точка с абсциссой 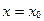 кривой кривой 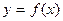 будет точкой перегиба, если будет точкой перегиба, если  или или  не существует и выполняется условие: не существует и выполняется условие:
| 1) 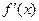 при переходе через точку при переходе через точку 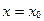 меняет знак;
2) меняет знак;
2)  ;
3) ;
3) 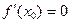 ;
4)* при переходе через точку ;
4)* при переходе через точку 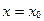 производная производная 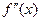 меняет знак;
5) меняет знак;
5) 
|
8. Вертикальной асимптотой графика функции  является прямая: является прямая:
| 1)  ; 2) ; 2)  ; 3) ; 3) 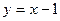 ; 4) ; 4)  ; 5)* ; 5)* 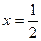
|

