Уравнение политропического процесса, уравнение Пуассона

Политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость С газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.

Для идеального газа уравнение политропы может быть записано в виде: 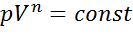или .

где величина 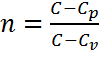называется показателем политропы, где .

В зависимости от процесса можно определить значение n:

1. Изотермический процесс: n = 1, так как PV¹ = const, значит PV = const, значит T = const.

2. Изобарный процесс: n = 0, так как PV⁰ = P = const.

3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона. Здесь γ — показатель адиабаты .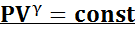

1атомный 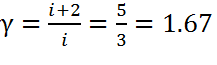2атомный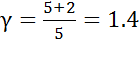

4. Изохорный процесс: 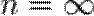, так как , значит P₁ / P₂ = (V₂ / V₁)ⁿ, значит V₂ / V₁ = (P₁ / P₂)^{(1 / n)}, значит, чтобы V₂ / V₁ обратились в 1, n должна быть бесконечность.

 

 

29.Термодинамическое определение энтропии

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение общего кол-ва тепла к величине абсолютной температуры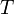

Например, при температуре 0 °C, вода может находиться в жидком состоянии и при незначительном внешнем воздействии начинает быстро превращаться в лед, выделяя при этом некоторое количество теплоты. При этом температура вещества так и остается 0 °C. Изменяется состояние вещества, сопровождающееся выделением тепла, вследствие изменения структуры.

Рудольф Клаузиус дал величине 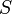имя «энтропия», происходящее от греческого слова τ ρ oπ ή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

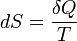где 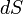— приращение (дифференциал) энтропии некоторой системы, а 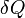— бесконечно малое количество теплоты, полученное этой системой.Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому 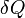считать полным дифференциалом нельзя.Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана

В 1877 году Людвиг Больцман установил связь энтропии с вероятностью данного состояния. Позднее эту связь представил в виде формулы Макс Планк:

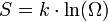где константа 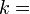1, 38·10− 23 Дж/К названа Планком постоянной Больцмана, а 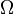— статистический вес состояния, является числом возможных микросостояний (способов) с помощью которых можно перейти в данное макроскопическое состояние. Этот постулат, названный Альбертом Эйнштейном принципом Больцмана, положил начало статистической механике, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы ( 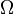) с одним из её термодинамических свойств ( 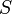).Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются.

 

⇐ Предыдущая123456

Поделиться: