
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Перестановки без повторений.
Перестановки - это комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком расположения этих элементов. Возьмем n различных элементов a1, a2, a3, … an; будем переставлять эти элементы всевозможными способами, оставляя без изменения число элементов и меняя только порядок их расположения. Обозначим общее число полученных таким образом перестановок P(n). P - первая буква французского слова permutation - перестановка. Составив таблицу перестановок для n элементов и применив (n - 1) раз правило произведения, получим число всех возможных перестановок: P(n) = n • (n -1) • (n - 2) • … • 3 • 2 • 1 = n! Такие перестановки называются перестановками без повторений (один и тот же элемент не может повториться в комбинации, все элементы различны). Задача: шесть человек могут в разном порядке сесть за круглый стол, сколько существует способов разместить эти шесть человек за столом? Решение: т.к. все люди различны и их комбинации различаются только порядком следования, то мы имеем перестановки без повторений. Определим их число: Р(6) = 6! = 1 • 2 • 3 • 4 • 5 • 6 = 720. Перестановки с повторениями Рассматривая различные перестановки, мы предполагали, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., nk элементов к-го вида, то имеем перестановки с повторениями, их число:
Задача: сколько различных «слов» можно составить из букв слова ДЕД, МАТЕМАТИКА. Решение: имеем перестановки с повторениями. А) ДЕД n=3, k=2, n1=2, n2=1 P3(2, 1) = 3! /(2! • 1! ) = 6 / 2 = 3; Б) МАТЕМАТИКА n=10, k=6, n1=2, n2=3, n3=2, n4=n5=n6=1 P10(2, 3, 2, 1, 1, 1)=10! /(2! • 3! • 2! )=2•4•5•6•7•9•10 = 134 400. Размещения Размещения без повторений. Размещениями называют комбинации, составленные из n данных элементов по k элементов (k< =n, k> 0), которые отличаются либо составом элементов, либо порядком расположения элементов. Обозначаются размещения Ank. А - первая буква французского слова arrangement, что в переводе означает " размещение", " приведение в порядок". Число всех возможных размещений находится по формуле: Задача: расписание одного дня состоит из двух пар. Определить число вариантов расписания при выборе из пяти дисциплин, если не может быть одинаковых пар. Решение: имеем размещения без повторений из пяти элементов по два, из число: Размещения с повторениями. Пусть существуют n различных элементов. Выберем из них m штук, действуя по следующему принципу: возьмем любой элемент, но не будем устанавливать его в какой-либо ряд, а просто запишем под номером 1 его название, сам же элемент вернем к остальным элементам. Затем опять из всех n элементов выберем один, запишем его название под номером 2 и снова вернем элемент обратно. Будем выполнять эти операции, пока не получим m названий. Размещения с повторениями вычисляются по формуле:
Задача: сколько четырехзначных номеров можно составить из 10 цифр? Решение: имеем размещения с повторениями из 10 элементов по 4, их число: Сочетания Сочетания без повторений. Сочетаниями называют комбинации, составленные из n различных элементов по k (k =< n) элементов, которые отличаются хотя бы одним элементом. Сочетания обозначаются: Cnk C - первая буква французского слова combinasion - сочетание. Составим из n элементов всевозможные сочетания по k элементов в каждом. Их будет Cnk. Внутри каждого сочетания, состоящего из k элементов, образуем всевозможные комбинации, учитывающие порядок следования в них элементов. Таких комбинаций будет Pk, т.к. мы в нашем сочетании образовываем перестановки. Всего различных комбинаций из n элементов по k в каждой, отличающихся друг от друга либо составом (элементами), либо порядком их следования, будет Cnk • Pk. Но такие комбинации называются размещениями. Таким образом, Ank = Cnk • Pk, тогда:
Задача: в шахматном турнире участвует 7 человек; сколько партий будет сыграно, если между любыми двумя участниками должна быть сыграна партия? Решение: имеем сочетания без повторений из 7 элементов по 2; их число: Сочетания с повторениями. Если в сочетаниях некоторые элементы (или все) могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями. Их число определяется по формуле: Задача: сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных? Решение: имеем сочетания с повторениями из четырех по 7 по, их число: 3. Графы.. 2 3.1. Основные понятия. 2 3.1.1. История теории графов. 2 3.1.2. Определения. 3 3.1.3. Смежности и инцидентность. 4 3.1.4. Изоморфизм графов. 5 3.2. Представление графов в ЭВМ.. 6 3.2.1. Требования к представлению графов. 6 3.2.2. Матрица смежности. 7 3.2.3. Матрица инциденций. 7 3.3. Геометрическая реализация графов. 8 3.4. Маршруты, цепи, циклы.. 8 3.4.1. Определения. 8 3.4.2. Эйлеровы графы.. 9 3.4.3. Гамильтоновы графы.. 10 3.5. Заключение. 12
Графы Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании. Дело в том, что теория графов предоставляет очень удобный язык для описания программных (да и многих других) моделей. Этот тезис можно пояснить следующей аналогией. Понятие отношения также можно полностью выразить через понятие множества. Однако независимое определение понятия отношения удобнее - введение специальных терминов и обозначений упрощает изложение теории и делает ее более понятной. То же относится и к теории графов. Стройная система специальных терминов и обозначений теории графов позволяют просто и доступно описывать сложные и тонкие вещи. Особенно важно наличие наглядной графической интерпретации понятия графа. Само название «граф» подразумевает наличие графической интерпретации. Картинки позволяют сразу «усмотреть» суть дела на интуитивном уровне, дополняя и украшая утомительные рациональные текстовые доказательства и сложные формулы. Основные понятия История теории графов Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач. 1 . Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку (рис. 3.1). Эта задача была решена Эйлером в 1736 году.
Рис. 3.1. Иллюстрация к задаче о Кенигсбергских мостах 2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 3.2). Эта задача была решена Куратовским в 1930 году.
Рис. 3.2. Иллюстрация к задаче о трех домах и трех колодцах Предметом первых задач теории графов были различные конфигурации, состоящие из точек и соединяющих их линий. При этом несущественно: являются ли эти линии прямыми или кривыми, длинными или короткими, тонкими или толстыми; важно только то, какие точки они соединяют. Т.о. граф – это абстрактное математическое понятие. Определения Графом G(V, E) называется совокупность двух множеств - непустого множества V ( множества вершин ) и множества Е неупорядоченных пар различных элементов множества V ( Е - множество ребер ). G(V, E): Число вершин графа G обозначим р, а число ребер – q. р(G) = |V| q(G) = |E|. Часто рассматриваются следующие родственные графам объекты. 1. Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным (или орграфом ). В этом случае элементы множества V называются узлами, а элементы множества 2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом). 3. Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом. Далее выражение: граф G(V, E) означает неориентированный граф без петель и кратных ребер. Обычно граф изображают диаграммой: вершины - точками (или кружками), ребра - линиями. Примеры. 1.
Т.о. это неориентированный граф с петлей и кратными ребрами. Рис. 3.3. Неориентированный граф с петлей и кратными ребрами. 2. Т.о. это ориентированный граф с петлей и кратными ребрами.
Рис. 3.4. Ориентированный граф с петлей и кратными ребрами.
3. 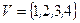 . .  , т.о. , т.о. 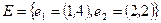
Рис. 3.5. Неориентированный граф с петлей.
Смежность и инцидентность Пусть v1, v2 - вершины, е = (v1, v2) - соединяющее их ребро. Тогда вершина v1 и ребро е инцидентны, вершина v2 и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. Степенью вершины v графа G(V, E) называется число ребер, инцидентных данной вершине. Обозначение: Вершина, имеющая степень 0 называется изолированной, имеющая степень 1 – висячей. Пример. Для графа, изображенного на рис. 3.5: вершина 3 – изолированная, вершины 1 и 4 - висячие. Пример. Для графа, изображенного на рис. 3.3. Ребро e1 инцидентно вершинам v1 и v2. Вершина v1 инцидентна ребрам e1 и e2. Ребра e1 и e2 – смежны. Вершины v1 и v2 – смежны.
Т.о. можно заметить, что Теорема Эйлера: Доказательство данной теоремы вытекает из того, что каждое ребро дает двойной вклад в сумму степеней вершин. Изоморфизм графов Говорят, что два графа G1(V1, E1) и G2(V2, E2) изоморфны (обозначается G1~ G2), если существует биекция h: V1 Графы рассматриваются с точностью до изоморфизма. Пример Три внешне различные диаграммы, приведенные на рис. 3.6, являются диаграммами одного и того же графа К3, 3.
Рис. 3.6. Диаграммы изоморфных графов Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, p(G) и q(G) - инварианты графа G. Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.
Рис. 3.8. Диаграммы неизоморфных графов с совпадающими инвариантами Представление графов в ЭВМ Следует подчеркнуть, что конструирование структур данных для представления в программе объектов математической модели - это основа искусства практического программирования. Мы приводим два различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Но все они, так или иначе, основаны на тех базовых идеях, которые описаны в этом разделе. Требования к представлению графов Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены два из наиболее часто используемых представления. Указанные представления пригодны для графов и орграфов, а после некоторой модификации также и для псевдографов, мультиграфов. Представления иллюстрируются на конкретных примерах графа G и орграфа D, диаграммы которых представлены на рис. 7.10.
Рис. 3.9. Диаграммы графа (слева) и орграфа (справа), используемых в качестве примеров Матрица смежности Представление графа с помощью квадратной булевской матрицы
отражающей смежность вершин, называется матрицей смежности, где
Пример
Матрица инциденций Представление графа с помощью матрицы Н: array [l..p, l..q] of 0..1 (для орграфов Н: array [l..p, l..q] of -1..1), отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа:
а для ориентированного графа
Пример
|
Последнее изменение этой страницы: 2017-03-15; Просмотров: 547; Нарушение авторского права страницы