
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Алгоритмы управления технологическим циклом (окончание)
6.1. Схемная реализация комбинационных схем на логических элементах Логическими элементами называют микросхемы малой степени интеграции, реализующие простейшие логические функции 2-4 аргументов. Наиболее распространены логические элементы, реализующие логические функции И (рис. 6.1а), ИЛИ (рис. 6.1б), И-НЕ (рис. 6.1в) и ИЛИ-НЕ (рис. 6.1г). Эти же логические функции реализуются путем применения сходных обозначений при программировании ПЛК на языке FBD (см. §8.3). Поэтому схемы на логических элементах являются удобными исходными алгоритмами при проектировании управляющих программ на языке FBD. К логическим элементам относят также микросхемы, реализующие простейшие последовательностные алгоритмы (например, триггеры), но они будут рассмотрены ниже. Логические элементы И реализуют функцию логического умножения (конъюнкцию). Это означает, что выходной сигнал схемы И равен единице только в том случае, когда все ее входные сигналы равны единице.
Рис.6.1. Схемные обозначения логических элементов
Логические элементы ИЛИ реализуют функцию логического сложения (дизъюнкцию), т.е. сигнал на выходе схемы ИЛИ равен нулю только тогда, когда все входные сигналы равны нулю. Логические элементы И-НЕ реализуют функцию инверсии логического произведения, а элементы ИЛИ-НЕ – функцию инверсии логической суммы. Таким образом, если логическое произведение равно единице, то элемент И-НЕ выдает нулевой сигнал на своем выходе, а если логическая сумма равна единице, то элемент ИЛИ-НЕ также выдает нулевой сигнал. В противном случае на выходах элементов данного типа формируется единичный сигнал. В одном корпусе микросхемы обычно имеется четыре логических схемы на два входа каждая, либо три схемы на три входа каждая, либо две схемы на четыре входа независимо от вида элементарных логических функций, которые данные микросхемы реализуют. Если не все входы логической схемы используются в проектируемом устройстве, то неиспользуемые входы следует объединять с используемыми. Так, для реализации функции инверсии необходимо объединить все входы схемы И-НЕ (см.рис. 6.2а). Тогда получим
Рис. 6.2. Реализация базовых логических функций на элементах И-НЕ
Если две схемы И-НЕ соединить последовательно, как показано на рис. 6.2б, то вторая схема инвертирует инверсию логического произведения, полученного на первой схеме, так что на выходе второй схемы получим само логическое произведение. Если же на вход схемы И-НЕ подать инверсии интересующих нас сигналов (см. рис. 6.2в), полученных предварительно с помощью опять же схемы И-НЕ, то на выходе получим логическую сумму исходных сигналов согласно закону де Моргана. Таким образом, с помощью элементов И-НЕ можно реализовать все базовые функции булевой алгебры, а следовательно – любые логические функции. Так же универсальны и элементы ИЛИ-НЕ. Элементы других типов, которые при наличии элементов И-НЕ или ИЛИ-НЕ не являются обязательными для реализации алгоритмов управления, имеют, как правило, специальное назначение. Так, элементы И (см. рис. 6.1а) обычно являются усилительными элементами. Их допустимый выходной ток достигает 100мА, в то время как обычные логические элементы имеют допустимый выходной ток до 5 мА. Пример 6.1. Реализовать на логических элементах преобразователь кода, логические функции которого отображаются формулами (5.2) – (5.5). Один из возможных вариантов схемы приведен на рис 6.3. Выходные сигналы датчика положения должны быть, прежде всего, инвертированы, чтобы их можно было подать во входные цепи преобразователя как в прямом, так и в инверсном виде. Соответственно, в левой части схемы (рис. 6.3а) показано, как входные сигналы Х1, Х2, Х3 и Х4 инвертируются на логических элементах D1/1, D1/2, D1/2 и D1/4, реализующих функцию И-НЕ в составе микросхемы D1. Схема, производящая непосредственное преобразование кода Грея, в котором работает датчик положения, в прямой арифметической двоичный код, удобный для использования в УВМ, приведена на рис. 6.3б. При построении схемы были учтены возможности использования отдельных ее цепей, реализующих функцию Y4, для реализации остальных заданных функций. Такие возможности видны при сравнении логических формул, реализующих заданные функции. Так, при сравнении выражений (5.5) и (5.6), видно, что у функций Y4 и Y2 имеются общие члены
а у функции Y1, согласно выражению (5.2), можно выделить кроме
Реализация самой функции Y4 значительно упростилась, поскольку было принято во внимание, что если обозначить То окажется, что
Поэтому достаточно реализовать функции а и b по формулам (6.1), а выражения Функция а реализована на элементах И-НЕ D2/1, D2/2 и D3/1. На выходах D2/1 и D2/2 получены соответственно инверсии
Аналогично на выходе D3/4 получено:
На выходах элементов D3/2 и D5/1, на входы которых поступают сигналы b и а, получены, соответственно, сигналы
реализуем функцию Y4 аналогично тому, как ранее реализовали функции а и b Однако на выходе структуры, реализующей Y4, ставим вместо элемента И-НЕ усилительный элемент И (элемента D6). Поэтому на первом выходе D6 получаем Инверсные сигналы на выходах нашей схемы позволяют организовать индикацию посредством сигнальных ламп. Действительно, если имеет место, например, Y4=1, то Функция Y2 легко реализуется подобно функции а, если обратить внимание на то, что выражение (5.6) преобразуется к виду
При реализации функции Y2 инверсию произведения Реализация функции Y1 проводится аналогично, но с учетом того, что выходной сигнал элемента D2/3 – это
а инвертируя его на элементе D4/1, получаем Вход C1 используется для синхронизации работы преобразователя кода с остальной системой управления.
Рис. 6.3. Схема преобразователя кода на логических элементах
6.2. Синтез алгоритмов последовательностных автоматов Последовательностными автоматами называют управляющие устройства, выходные сигналы которых зависят не только от комбинации входных сигналов, имевших место в текущем такте технологического цикла, но и от комбинаций входных сигналов, имевших место в предыдущих тактах и повлиявших на внутреннее состояние автомата. Так, при перемещении рабочего органа станка по линейной траектории и достижении заданной точки рабочей зоны станка, система программного управления переходит к выполнению нового кадра программы, в котором может быть задано опять же перемещение по линейной траектории, но в другом направлении и с другой скоростью. Сигналом к переходу на отработку нового кадра программы является в этом случае совокупность сигналов датчиков положения о достижении заданной точки в пространстве. В простейших последовательностных автоматах, которые далее будем называть просто автоматами, программа работы жестко закладывается в конструкцию автомата и определяет последовательность смены его состояний, или тактов. Каждое состояние автомата характеризуется отличным от соседнего состояния способом реагирования на поступающие входные сигналы. Переход от одного состояния к другому определяется как комбинацией входных сигналов, так и конкретным состоянием, в котором находится автомат. Самым простым способом смены состояний является случай, когда все состояния (или такты) пронумерованы и их смена производится в порядке возрастания (или уменьшения) номеров. Запоминание состояний автомата обычно производится с помощью двоичных элементов памяти, таких как электронный триггер или электромагнитное реле. Число состояний, которые можно запомнить с помощью совокупности из m таких элементов достигает М=2m, так что количество запоминающих элементов m выбирается исходя из неравенства m ≥ log2M, (6.2) где M – количество состояний, которые подлежат запоминанию.
Рис.6.4. Общая структура последовательностного автомата
Если обозначить через Х совокупность сигналов обратной связи (входных сигналов), поступающих от ТО, через Y- совокупность сигналов управления (выходных сигналов), подаваемых на ТО, через Z – совокупность внутренних управляющих сигналов, отображающих текущее состояние автомата, то окажется, что одним и тем же значениям Х соответствуют различные значения Y, если при тех же Х значения Z различны. Общая структура последовательностного автомата приведена на рис. 6.4. Видно, что автомат состоит из двух основных блоков: арифметико-логического устройства (АЛУ) и устройства формирования состояний (УФС). Блок АЛУ является комбинационной частью последовательностного автомата. Он производит заданные арифметические и логические операции над входными сигналами Хt и управляющими сигналами Zt-1, причем у простейших автоматов производятся только логические операции. Устройство формирования состояний автомата (УФС), действуя посредством совокупности управляющих сигналов Zt-1, задает операции которые должно произвести АЛУ над входными сигналами Хt в текущем рабочем такте. Выходные сигналы АЛУ подразделяются на две группы: Yt и Zt, причем индекс t означает момент времени или номер такта, в котором были выработаны данные сигналы. Сигналы Yt – это управляющие сигналы, подаваемые на технологический объект, а сигналы Zt - это внутренние управляющие сигналы, характеризующие внутреннее состояние автомата. Они подаются, совместно с некоторыми сигналами Yt, в УФС и там запоминаются. Далее эти сигналы обрабатываются в соответствии с действиями, предусмотренными очередным кадром управляющей программы УП, и подаются на вход АЛУ после прихода очередного тактового импульса С на вход синхронизации. Синхронизация предотвращает подачу управляющих сигналов Zt-1 до того, как они будут полностью сформированы в УФС. После того, как они сформируются и будут поданы в АЛУ, в УФС смогут поступить новые сигналы Zt и Yt, сигналы следующего такта управления. Следовательно, управляющие сигналы Zt-1 на входе АЛУ относятся к предыдущему такту работы АЛУ, что и отражается индексом t-1. У простейших автоматов внешняя УП после задания режима работы в УФС не поступает. Их поведение в технологическом цикле целиком определяется распределением сигналов Yt и Zt, которые поступают в УФС и там запоминаются. После подачи тактового импульса на вход С совокупность сигналов Z (часть которых может совпадать с выходными сигналами Y) поступает на входы АЛУ, задавая логические операции, которые оно должно совершить в течение нового рабочего такта. У очень простых автоматов, работающих по принципу асинхронного управления, особый генератор тактовых импульсов отсутствует, а гонка импульсов предотвращается тем, что при любых переходах из одного состояния в другое допускается изменение значения только одного сигнала из всей совокупности внутренних управляющих сигналов Z. В этом случае изменение очередного сигнала zi из совокупности Z является как бы синхронизирующим импульсом, задающим функционирование АЛУ в новом такте ti+1 работы автомата. Алгоритм последовательностного автомата удобно составлять исходя из структурной схемы, приведенной на рис. 6.4. На этой схеме АЛУ является комбинационной частью автомата, а УФС включает в себя запоминающие устройства (ЗУ), задающие посредством сигналов Zt-1 режим работы АЛУ в каждом рабочем такте автомата в течение технологического цикла. В простейших автоматах сигналы Zt-1 – это сигналы Zt и, возможно, часть сигналов Yt, сформированные в предыдущем такте автомата и запомненные в УФС. Следовательно, составление алгоритма простого автомата естественным образом разделяется на два этапа. На первом этапе составляется алгоритм функционирования АЛУ в виде Yt = f1(Xt, Zt-1); Zt = f2(Xt, Zt-1) по правилам составления комбинационных схем, а затем на втором этапе уточняется структура ЗУ в составе УФС и порядок формирования синхронизирующих импульсов. Функцию Yt принято называть функцией выходов, а функцию Zt – функцией переходов от состояния к состоянию автомата. В качестве примера синтеза простого автомата рассмотрим составление схемы триггерной ячейки, являющейся основой микропроцессорных запоминающих устройств. Простейшей триггерной ячейкой является асинхронный RS-триггер. Это ячейка с двумя входами, R и S, и с двумя выходами: прямым выходом Q и инверсным выходом Таблица 6.1 Таблица выходов RS-триггера
Функционирование RS-триггера может быть отображено таблицей выходов 6.1. В табл. 6.1 видно, что при R=0 и S=0 RS-триггер сохраняет свое состояние неизменным, т.е. хранит ранее записанную информацию: либо Q=0, либо Q=1. При подаче сигнала St=1 на выходе устанавливается Qt=1, вместо Qt=0 или сохраняется Q=1. Аналогично при подаче Rt=1 на выходе устанавливается Q
Вторые части формул (6.3) и (6.4) позволяют непосредственно по ним получить схему RS-триггера на элементах И-НЕ, приведенную на рис. 6.5. Действительно, на выходе
а на выходе Qt соответственно получим
что соответствует выражению (6.3).
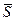
Qt
Рис. 6.5. Схема RS-триггера на элементах И-НЕ
Аналогично проверяется правильность выражения (6.4) относительно выхода
Лекция 7 |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 392; Нарушение авторского права страницы