
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ИССЛЕДОВАНИЕ КОРРЕЛЯЦИОННОЙ ЗАВИСИМОСТИСтр 1 из 5Следующая ⇒
Цель работы - привить навыки по обработке полученных экспериментальным путем статистических данных для определения мер тесноты связи случайных величин, а также определения уравнений регрессии по методу Чебышева. Общие положения 1.1. Общие сведения о корреляции В природе все явления взаимосвязаны. Различают связи функциональную и корреляционную. Функциональной называют такую связь между величинам которой каждому значению одной переменной соответствует условное распределение другой. Статистическое исследование корреляции сводят к установлению факт между случайными величинами, определению ее формы, направленности и ты. Установление факта связи производят на основе физического анализа результатов измерений соответствующих величин. Корреляцию называют простой, если она основана на связи двух случайных величин, и множественной, если имеется взаимосвязь нескольких случайных величин. По форме различают корреляцию линейную, когда зависимость между случайными величинами отражается в виде уравнения прямой, и криволинейную - она отражается в виде уравнения какой-либо кривой. По направлению различают корреляцию прямую, когда с увеличением одной случайной величины увеличивается и другая, и обратную, когда с увеличением одной случайной величины другая в среднем уменьшается. Тесноту корреляционной связи выражают в виде отвлеченных статистических характеристик (показателей) - коэффициента корреляции r и корреляционного отношения Коэффициент корреляции является численной характеристикой линейной корреляции и может быть найден по формуле
где X При обработке на ЭВМ выражение (3.1) удобнее представить в другом виде
Коэффициент корреляции может принимать значение от -1 до +1. При полной прямой корреляции (корреляция переходит в функциональную зависимость) r = +1, при полной обратной (тоже функциональная зависимость) r = -1. При r = 0 прямолинейная корреляционная связь отсутствует (криволинейная связь при этом может быть). Обычно считают при r
а при N Корреляционное отношение является численной характеристикой криволинейной связи. Квадрат корреляционного отношения представляет собой частное от деления двух дисперсий
где В случае функциональной линейной связи Конечной целью статистического корреляционного анализа является установление корреляционного (когда обе случайные величины имеют центрированный нормированный вид) или регрессионного (когда обе случайные величины даны в произвольном исчислении) уравнения. Сделать это можно несколькими способами, из которых наиболее удобен метод Чебышева. Пояснения будем вести на примере выборки большого объема.
1.2. Предварительная группировка данных Пусть при изготовлении некоторой продукции одного типономинала одновременно измеряются два параметра, значения которых представлены в таблице 1.1. Для удобства дальнейшей обработки данных ее необходимо упорядочить и представить в виде таблицы двумерного распределения (таблица 3.1). Для этого по гистограмме лабораторной работы 1 строим таблицу с числом внутренних клеток 9 Таблица двумерного распределения дает дополнительную возможность избавиться от грубых промахов, которые невозможно выявить в одномерных выборках. Для двумерной таблицы грубым промахом считается попадание в клетку, отстоящую от основного массива данных одновременно не менее чем на одну пустую клетку по горизонтали и по вертикали (при достаточно большом общем объеме выборки, например, не менее 100). Воспользовавшись формулами (1.5) и (1.6) для обеих гистограмм величины найдем
Тогда по формуле (3.4) квадрат корреляционного отношения Таблица 3.1 - Таблица двумерного распределения
1.3. Метод Чебышева Метод Чебышева позволяет аппроксимировать искомую зависимость в виде полинома некоторой степени. Исследование связи между случайными величинами начинается с вычисления смешанных моментов различных порядков. Смешанным центральным моментом порядка (hx, h
Полагая h Смешанные основные моменты порядка (
В частности, смешанный основной момент порядка (1/1) В результате вычислений находим
Значимость коэффициента корреляции при объемах выборки N> 50 можно установить при соблюдении неравенства
где В нашем случае В случае, если коэффициент корреляции достаточно велик, правильность вычислений можно установить при подтверждении неравенства П.Л. Чебышев предложил достаточно простой и удобный способ определения уравнения регрессии по найденным моментам различного порядка, корреляционному отношению и коэффициенту корреляции. Способ предполагает предварительно найти корреляционное уравнение приближенного условного основного момента
где
Следует иметь в виду, что при доказанном нормальном распределении случайной величины X смешанные основные моменты Переход к уравнению регрессии выполняется по формуле
где Выражение (3.8) является корреляционным уравнением в силу того, что аргумент и функция выражены в относительных единицах (в центрированном и нормированном виде). Выражение (3.9) является уравнением регрессии той же пары в абсолютных единицах измерения с учетом среднеквадратических отклонений. Именно по этой причине регрессия есть линия - геометрическое место точек проекций центров условных распределений (см. рис. 3.1) Выражение (3.8) дает возможность подобрать полином любого (в разумных пределах) порядка, так как построен он следующим образом: для полинома первой степени достаточно принимать в расчет только первый член выражения (3.8), остальными можно пренебречь; для полинома второго порядка - первые два члена и т.д. (Здесь мы ограничились уравнениями только второго порядка). Показателем того, на каком порядке корреляционного уравнения следует остановиться, служит критерий Для определения порядка корреляционного уравнения находим критерий линейности
с основной ошибкой
Так как
с основной ошибкой
Так как критерий и его основная ошибка отличаются друг от друга не более чем в 3 раза, то с достаточной точностью можно считать искомое корреляционное уравнение квадратичным. Подставляя найденные значения символов в (3.8), получим
Подставляя найденное выражение в (3.9) и раскрывая значение
Ошибка уравнения второй степени (границы существования вероятного значения случайной величины Y, коридор ошибок уравнения регрессии) равна
Для наглядности найденное уравнение регрессии и его коридор ошибок изображены на рисунке 3.1.
Рисунок 3.1 - Графическое изображение найденного уравнения регрессии, коридора существования и групповых средних Порядок проведения работы 2.1. По таблице 1.1 массива экспериментальных данных, полученной у преподавателя, построить таблицу двумерного распределения. 2.2. Вычислить среднюю арифметическую 2.3. Вычислить корреляционное отношение 2.4. Вычислить основные моменты двумерного распределения 2.5. Определить порядок корреляционного уравнения и найти уравнение регрессии по методу Чебышева. 2.6. Построить график уравнения и коридор его существования. 2.7. Оценить полученные результаты. Содержание отчёта Отчет о лабораторной работе должен содержать исходную таблицу данных, таблицу двумерного распределения, результаты вычислений по п.2.2 - 2.5 и графики по п.2.6. При подготовке к защите лабораторной работы необходимо ознакомиться с контрольными вопросами и продумать ответы на них. 4. Контрольные вопросы 4.1. Назовите виды и степени связи между случайными величинами. 4.2. Что такое коэффициент корреляции и корреляционное отношение? В чём их сходство и различие? 4.3. Что выражают смешанные моменты? Как определяется их порядок? Kaкие смешанные моменты Вы знаете? 4.4. В чем идея метода Чебышева по нахождению уравнения регрессии? 4.5. Что такое корреляционное уравнение и чем оно отличается от регрессионного? От обычного алгебраического уравнения? 4.6. Как определяется степень уравнения регрессии и как проверяется ее достаточность? 4.7. Что такое доверительные границы (коридор ошибок) уравнения регрессии? Как проявляется правильность их нахождения? 5. Рекомендуемая литература 5.1. Митропольский А.К. Техника статистических вычислений. Изд. 2-е. – М.: Наука, 1971. - 576 с. (С.86-107, 133-141, 359-366, 395-404). 5.2. Математическая статистика /Под ред. проф. A.M. Длина. -М.: Высшая школа. 1975. - 270 с. (С. 269-299). 5.3. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике науке: Методы обработки данных /Пер. с англ.; Под ред. Э.К.Лецкого. - М.: Мир 1980. - 610 с. (С.447-465, 472-482). 5.4. Долгов Ю.А. Статистическое моделирование: Учебник для вузов. – 2-е изд., доп. - Тирасполь: Полиграфист, 2011.- 352 с. (с. 39-53). Лабораторная работа № 4 ПАРАБОЛИЧЕСКОЕ СГЛАЖИВАНИЕ Цель работы – привить навыки по обработке двумерных экспериментальных данных, аргументы которых носят периодический (равноотстоящий) характер, в том числе с пропусками. Общие положения 1.1. Методы расчета при равноотстоящих значениях аргумента На практике часто встречаются случаи, когда необходимо найти зависимость какой-либо переменной (случайной величины) от другой случайной величины, числовые значения которой отстоят друг от друга на равных расстояниях (долях, частях), то есть, соблюдается равенство
X2 - X1=X3 - X2=…=Xn - Xn-1= DX. (4.1)
Это могут быть задачи об изменениях цен, урожая, количества осадков и т.п. по годам или любые другие задачи, лишь бы соблюдалось равенство (4.1). В этом случае легко весь класс таких задач свести к единому аргументу, преобразовав именованные случайные величины Xi в абстрактные номера интервалов xi
где Xн = Xmin - DX – начальное значение аргумента. Для решения таких задач П.Л. Чебышев предложил простой способ отыскания функции
f(x) = k0 + k1y1(x) + k2y2(x) + … + klyl(x), (4.3)
где l £ n-1, причём n - количество интервалов;
- - - - - - - - - - - - - - -
Согласно формуле (4.3) первый член суммы является средним арифметическим выборки по случайной величине Y, первые два члена представляют собой линейное уравнение, три члена – квадратичное и т.д. Прибавляя к функции по одному новому члену мы увеличиваем степень уравнения на единицу. Для практических целей достаточно параболы 2-го или 3-го порядка, поэтому дальнейшие разложения полинома yl(x) здесь не приводятся. Наилучшая кривая сглаживания считается полученной при достижении минимума ошибки приближения параболы
где
Проверку полученного уравнения на степень приближения к экспериментальным данным можно вести по критерию c2-Пирсона, методика работы с которым изложена в разделе 1.3. Пример 1. По числовой выборке середины разрядов Р е ш е н и е: Для нахождения уравнения связи воспользуемся формулами (4.3)-(4.4). Результаты вычислений для удобства будем записывать в специальную таблицу. 0) Вычисление параболы нулевого порядка.
1) Вычисление параболы первого порядка.
При сложении первого и второго члена суммы (4.3) получается:
Так как s1< s0, то вычисления следует продолжать. 2) Вычисление параболы второго порядка.
При сложении третьего члена суммы (4.3) с предыдущими получается:
Так как s2< s1, то вычисления следует продолжать. 3) Вычисление параболы третьего порядка.
При сложении четвёртого члена суммы (4.3) с предыдущими получается:
Таблица 4.1 Последовательность вычислений параболического сглаживания для равноотстоящих значений аргумента
Так как s3> s2, то вычисления прекращаются и формально наилучшим считается уравнение второго порядка. Однако в силу того, что s2»s3 это ещё надо доказать. С этой целью подсчитаем значения функций 2f(x) и 3f(x) (см. таблицу), а затем по выражению (1.13) и таблице 1.2 определим для каждого из уравнений величину c2, по которой найдём вероятность правильной аппроксимации. Для нашего примера это Р(2c2)=0, 99951 и Р(3c2)=0, 99967. Так как табл.А.1 для такой точности не приспособлена, то пришлось воспользоваться таблицами в [4]. Такие вероятности означают, что с точностью до 0, 1% оба уравнения равноценны. В этом случае предпочтение нужно отдавать простейшему из них
которое, при подстановке первичного преобразователя
Сравнение этого уравнения с ранее найденными в лабораторной работе №3 показывает практически полное их совпадение. Коридор существования найденного уравнения можно определить по формуле
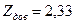 соответствует соответствует  , а , а  рассчитано при определении параболы второго порядка. Графическая интерпретация результатов работы представлена на рисунке 4.1. рассчитано при определении параболы второго порядка. Графическая интерпретация результатов работы представлена на рисунке 4.1.
Рисунок 4.1 – Графическое изображение найденного уравнения регрессии, коридора его существования и средних экспериментальных точек 1.2. Методы расчета при неравноотстоящих значениях аргумента В экспериментальной работе случается так, что некоторые данные в определённые моменты времени измерить нельзя (или забыли, или получился грубый промах и т.п.). Тогда в череде равноотстоящих аргументов исчезает чёткая последовательность xi=1, 2, …, n по числам натурального ряда и образуются как бы «дыры». При таком положении дел воспользоваться методикой расчёта, приведённой в подразделе 2.5.1, нельзя, результат будет неверным. В неё надо внести коррективы. Предлагается (по аналогии) искать уравнение в виде
где l £ n – 1; n – объём выборки; q1(x) = x ; q2(x) = x2 - B2x – A2 ; q3(x) = (x – B3) × q2(x) – A3 × q1(x);
Остальные действия и критерии такие же, как и в случае равноотстоящих аргументов. Пример 2. По числовой выборке середины разрядов Р е ш е н и е: Для нахождения уравнения связи воспользуемся формулами (4.5). Результаты вычислений для удобства будем записывать в специальную таблицу. 0) Вычисление параболы нулевого порядка.
1) Вычисление параболы первого порядка.
Так как s1< s0, то вычисления следует продолжать. Таблица 4.2 - Последовательность вычислений параболического сглаживания для неравноотстоящих значений аргумента
2) Вычисление параболы второго порядка.
Так как s2< s1, то вычисления следует продолжать. 3) Вычисление параболы третьего порядка.
Так как s3> s2, то вычисления прекращаются. Необходимо вернуться к уравнению второго порядка. Как правило, при неравноотстоящих аргументах третий порядок даёт либо незначительное уменьшение ошибки, либо резкое её возрастание, поэтому можно останавливаться на уравнениях второго порядка без расчёта уравнения третьего порядка. Это подтверждается проверкой на совпадение уравнения с исходными (экспериментальными) данными по критерию Пирсона Р(2c2)=0, 9999. Обратным преобразованием получаем
или, переходя к первоначальным обозначениям,
Сравнение полученного уравнения с ранее найденными показывает практически полное их совпадение. Расчет коридора существования и графическая интерпретация результатов аналогичны предыдущим. Порядок проведения работы 2.1. По данным таблицы 3.1 из лабораторной работы №3 найти шаг 2.2. Вычислить элементы параболы нулевого порядка и заполнить соответствующие графы таблицы 4.1. 2.3. Вычислить элементы параболы первого порядка, найти линейное уравнение и заполнить соответствующие графы таблицы 4.1. 2.4. Вычислить элементы параболы второго порядка, найти квадратичное уравнение и заполнить соответствующие графы таблицы 4.1. |
Последнее изменение этой страницы: 2017-04-12; Просмотров: 656; Нарушение авторского права страницы